首页理论教育任意角三角函数|机电应用数学

任意角三角函数|机电应用数学

2023-11-22 理论教育版权反馈

【摘要】：1.任意角的三角函数的定义在本章的2.2节已经讨论了锐角的三角函数值，但是把角的概念推广以后，角可以为任意大小，那么对于任意角α，又该如何确定其三角函数值呢？

1.任意角的三角函数的定义

在本章的2.2节已经讨论了锐角的三角函数值，但是把角的概念推广以后，角可以为任意大小，那么对于任意角α，又该如何确定其三角函数值呢？下面就来研究这个问题.

如图2-15所示，将角a置于平面直角坐标系中，使角的顶点与原点重合，角的始边与x轴非负半轴重合，并设角α终边上任意一点P（不含点O）的坐标为（x，y），则它与原点的距离为

，我

们定义角α的三角函数如下：

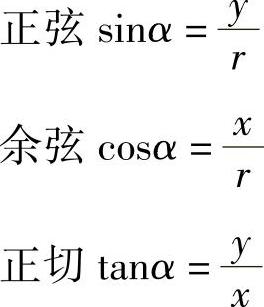
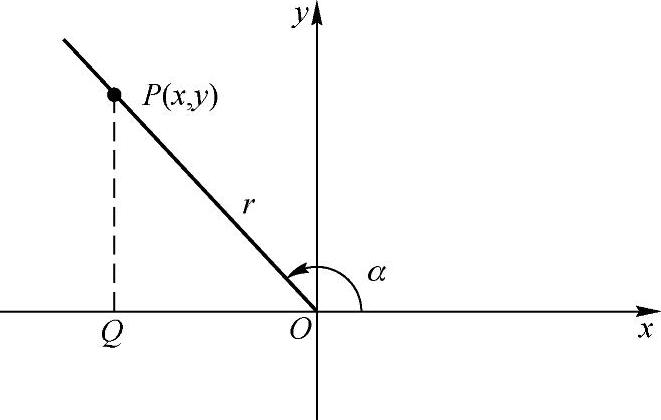
图2-15

其中，对于tanα，x不能为零，即点P的横坐标不能为零，角α的终边不能在y轴上.

例1　已知角α的终边经过点P（2，-3），求α的三个三角函数值.

解：因为x=2，y=-3，所以，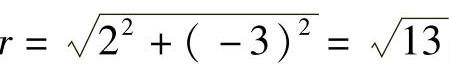

于是，，

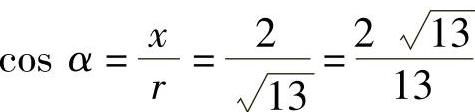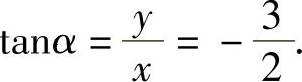
做一做

根据下列条件，分别求角α的三个三角函数值，并回答第（4）个问题：

（1）角α的终边上有一点P₁（-3，-4）；

（2）角α的终边上有一点P₂（-6，-8）；

（3）角α的终边上有一点P₃（-9，-12）；

（4）一个角的三角函数值与这个角终边上的点得位置有关吗？

特别地，当角的终边落在坐标轴上时，由定义我们可以得到它们所对应的三角函数值（见表2-4）.

表2-4

例2　计算2sin90°-3cos0°+4sin270°+7cos180°.

解：原式=2×1-3×1+4×（-1）+7×（-1）

=2-3-4-7

=-12.

练一练

计算下列各式：

（1）sin180°+cos180°+tan180°；

（2）2sin90°-3cos0°+4sin270°+7cos180°；

（3）asin0°+bcos90°+ctan180°.

2.任意角的三角函数值的符号

由任意角的三角函数的定义，以及各象限内点的坐标的符号，我们可以得到：

1）正弦值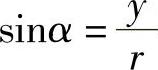

在第一、二象限为正（y>0，r>0），在第三、四象限为负（y<0，r>0）；

2）余弦值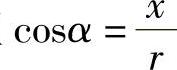

在第一、四象限为正（x>0，r>0），在第二、三象限为负（x<0，r>0）；

3）正切值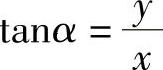

在第一、三象限为正（x，y同号），在第二、四象限为负（x，y异号）.

例3　确定下列三角函数值的符号：(www.chuimin.cn)

（1）cos250°；（2）sin（-45°）；（3）tan（-672°）；（4）tan660°.

解：（1）因为250°是第三象限角，所以cos250°<0；

（2）因为-45°是第四象限角，所以sin（-45°）<0；

（3）因为-672°是第一象限角，所以tan（-672°）>0；

（4）因为660°是第四象限角，所以tan660°<0.

练一练

确定下列三角函数值的符号：

（1）sin110°；（2）cos230°；（3）tan525°；（4）sin（-30°）.

3.同角三角函数基本关系式

由三角函数的定义，我们可以得到下列同角三角函数的基本关系式.

（1）商数关系

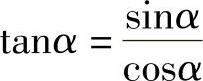
（2）平方关系

sin²α+cos²α=1

上述关系式是恒等式，即当α取使关系式两边都有意义的任意值时，关系式两边的值相等.

例4　已知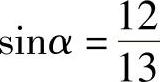

，并且α是第二象限角，求cosα和tanα.

解：因为sin²α+cos²α=1，所以

又因为α是第二象限角，所以cosα<0，即有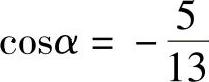，从而

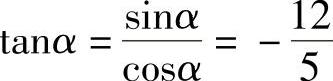
练习

1.已知锐角α终边上一点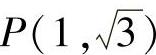，求角α.

2.若sinθ·cosθ>0，则θ应在第几象限？

3.已知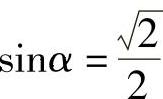，且α是第二象限角，求cosα，tanα.

4.计算：5cos180°-3sin90°+2tan0°-6sin270°.

习题四

1.已知角α的终边分别经过下列各点，试求α的三个三角函数值：

（1）P（1，1）；

（2）；

（3）P（-5，-12）；（4）P（4，3）.

2.计算：

（1）sin90°-cos180°+sin270°-cos0°；

（2）4cos90°-3sin270°-5cos180°+3sin0°.

3.确定下列三角函数值的符号：

（1）sin130°；（2）cos200°；（3）tan420°；（4）sin（-120°）；

（5）cos2025°；（6）tan590°.

4.已知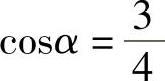，且α是第四象限的角，求sinα和tanα的值.