角度推广：30°角的表示方法

2023-11-22 理论教育版权反馈

【摘要】：与30°角有相同的始边和终边的角可以怎样表示呢？

引例

在生活中，有很多物体都给我们以角的印象，比如三角板的三个角、钟表的时针和分针所成的角等（见图2-9）.

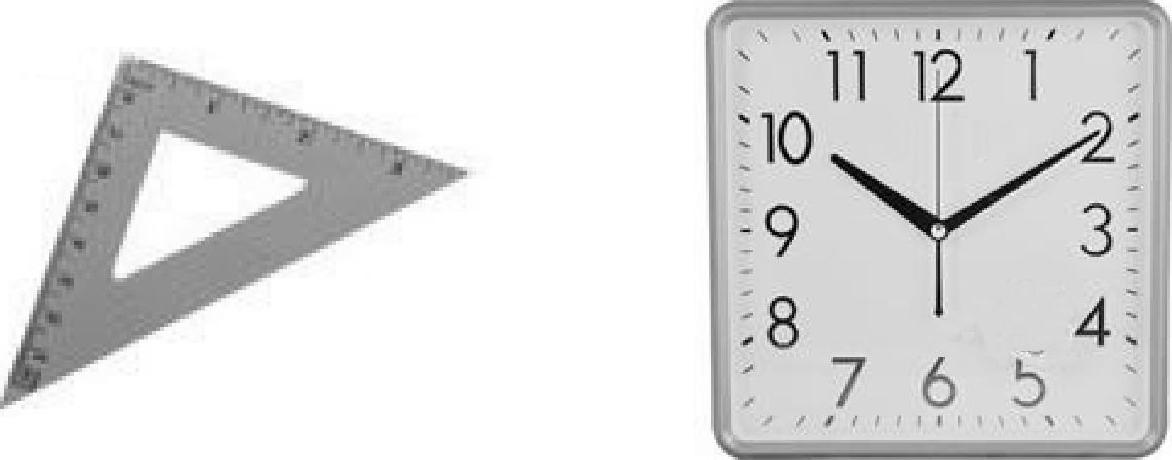
图2-9

我们知道，在平面内，角可以看做一条射线绕着它的端点旋转而成的图形.旋转起始时的射线叫做角的始边，终止时的射线叫做角的终边，射线的端点叫做角的顶点.

如图2-10所示，OA是角α的始边，OB是角α的终边，O是角α的顶点.

如图2-11所示，O′A′是角β的始边，O′B′是角β的终边，O′是角β的顶点.

图2-10

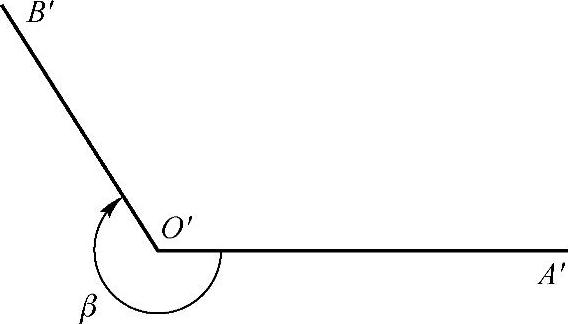
图2-11

角除了用常用英文大写字母A，B，C等表示外，也可以用希腊字母α，β，γ等表示，特别是当角作为变量时，常用字母x表示.

在初中阶段我们学习过0°～360°的角，即如果α=90°，那么α叫做直角；如果0°<α<90°，那么α叫做锐角；如果90°<α<180°，那么α叫做钝角；如果α=180°，那么α叫做平角；如果α=360°，那么α叫做周角.

但是在实际问题中，经常会遇到大于360°的角和按不同方向旋转所成的角，例如，体操运动员和跳水运动员的“转体一周半动作”；钟表的秒针走过1.5min时；自行车轮子转两周时，等等（见图2-12）.

显然，这些转过的角已远远超过360°，那这样的角又该怎样描述呢？

图2-12

在平面内，一条射线绕它的端点有两个旋转方向：顺时针方向和逆时针方向.习惯上规定，按逆时针旋转而成的角叫做正角；按顺时针方向旋转而成的角叫做负角；当射线没有旋转时，我们也把它看成一个角，叫做零角，记为0°.

如图2-13所示，射线OA绕点O按逆时针方向旋转45°到OB的位置，所形成的角可记作∠AOB=45°；射线OA绕端点O按顺时针方向旋转30°到OC的位置所形成的角记作∠AOC=-30°

在画图时，我们常用带箭头的弧来表示旋转生成的角，如图2-14所示，α=450°，β=-330°

至此，我们把角的概念推广到任意大小的正角、负角和零角的范围.

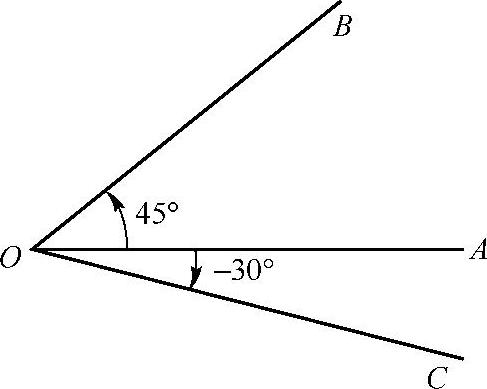
图2-13

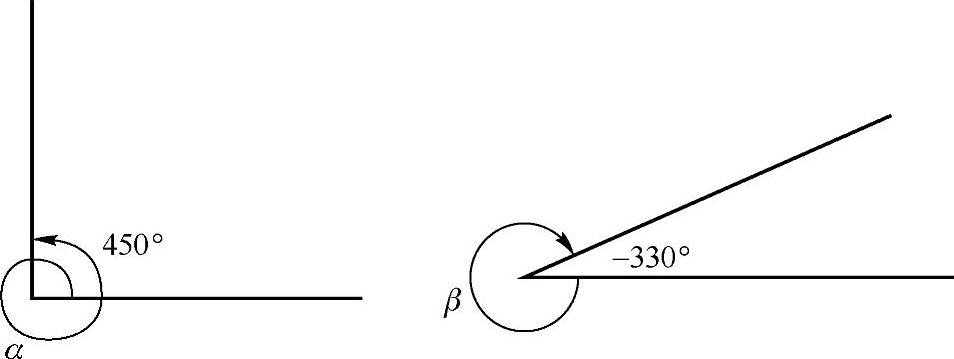
图2-14

为了讨论问题的方便，我们往往在平面直角坐标系中来讨论角，具体做法是将角的顶点与坐标原点重合，角的始边与x轴的正半轴重合，这样一来，角的终边落在第几象限，我们就说这个角是第几象限的角（角的终边落在坐标轴上，则此角不属于任何一个象限，我们称其为轴线角）.

例如，30°，390°，-330°是第一象限角；-195°，120°是第二象限角；585°，1280°是第三象限角；300°，-60°是第四象限角；90°，0°，-180°都是轴线角.

练一练

请在平面直角坐标系中作出45°，150°，270°，-210°，-300°的角，并分别说出它们各是第几象限角.

试一试

在坐标系中作出390°，-330°角，观察它们的终边与30°角的终边的关系如何？与30°角有相同的始边和终边的角可以怎样表示呢？

这些角可以分别表示成

-330°=30°-360°

30°=30°+0×360°(www.chuimin.cn)

390°=30°+1×360°

750°=30°+2×360°

︙

所有这些角可以表示成α=30°+k·360°（k∈Z）.

一般地，所有与角α终边相同的角，连同角α在内，可以表示成α+k·360°（k∈Z）

即任一与α终边相同的角，都可以表示成角α与整数个周角的和.

例：在0°～360°范围内，找出与下列各角终边相同的角，并判定它们是第几象限角.

（1）-120°；（2）640°；（3）-950°12′.

解：（1）因为-120°=240°-360°，

所以与-120°角终边相同的角是240°角，它是第三象限的角；

（2）因为640°=280°+360°，

所以与640°终边相同的角是280°，它是第四象限的角；

（3）-950°12′=129°48′-3×360°，

所以与-950°12′角终边相同的角是129°48′，它是第二象限角.

练习

1.已知角的顶点与坐标系的原点重合，始边落在x轴的正半轴上，作出下列各角，并指出它们是哪个象限的角：

（1）375°；（2）-80°；（3）-585°；（4）202°39′.

2.在0°～360°范围内，找出与下列各角终边相同的角，并指出它们是哪个象限的角：

（1）780°；（2）-460°；（3）435°20′.

习题三

1.时针走过3h 20min，则分针所转过的角的度数为，时针所转过的角的度数为.

2.锐角是第几象限的角？第一象限的角是否都是锐角？小于90°的角是锐角吗？

3.已知角的顶点与坐标系的原点重合，始边落在x轴的正半轴上，作出下列各角，并指出它们是哪个象限的角：

（1）420°；（2）-75°；（3）855°；（4）-510°.

4.在0°～360°范围内，找出与下列各角终边相同的角，并指出它们是哪个象限的角：

（1）-265°；（2）1185°14′；（3）-843°10′；（4）2903°15′；

（5）360°；（6）720°；（7）1080°；（8）1440°.

5.判断正误：

（1）第一象限的角一定不是负角；（）

（2）第二象限角一定是钝角；（）

（3）第四象限角一定是负角；（）

（4）若β=α+k·360°（k∈Z），则α与β终边相同.（）

角度推广：30°角的表示方法

相关推荐