首页 理论教育探索锐角三角函数，机电应用数学

探索锐角三角函数，机电应用数学

2023-11-22 理论教育 版权反馈
【摘要】：探索直角三角形的边角关系直角三角形是我们生活中经常接触的图形，如果只知道直角三角形的一条边和一个锐角，你能求出其他的边和角吗？实例2：图2-5是两个自动扶梯，甲、乙两人分别从1号和2号自动扶梯上楼，谁先到达楼顶？练习1.在等腰三角形ABC中，AB=AC=5，BC=6，求sinB，cosB，tanB.2.在△ABC中，∠C=90°，，BC=20，求△ABC的周长.试一试两块不同的三角尺中有几个不同的锐角？

探索直角三角形的边角关系

直角三角形是我们生活中经常接触的图形，如果只知道直角三角形的一条边和一个锐角，你能求出其他的边和角吗？

实例1：随着改革开放的深入，上海的城市建设正日新月异地发展，一幢幢大楼拔地而起.比如上海环球金融中心（见图2-4）就是上海的一座摩天大楼.你能应用数学知识和适当的途径得到金融中心的实际高度吗？

实例2：图2-5是两个自动扶梯，甲、乙两人分别从1号和2号自动扶梯上楼，谁先到达楼顶？如果AB和A′B′相等，∠α和∠β大小不同，那么它们的高度AC和A′C′相等吗？AB，AC，BC与∠α，A′B′，A′C′，B′C′与∠β之间有什么关系呢？

生活中除了上述两个实例，还有很多事情都与直角三角形的边和角有关，因此我们定义：

在Rt△ABC中（见图2-6），如果锐角A确定，那么∠A的对边与斜边的比、邻边与斜边的比也随之确定.

978-7-111-45466-3-Chapter02-23.jpg

图2-4

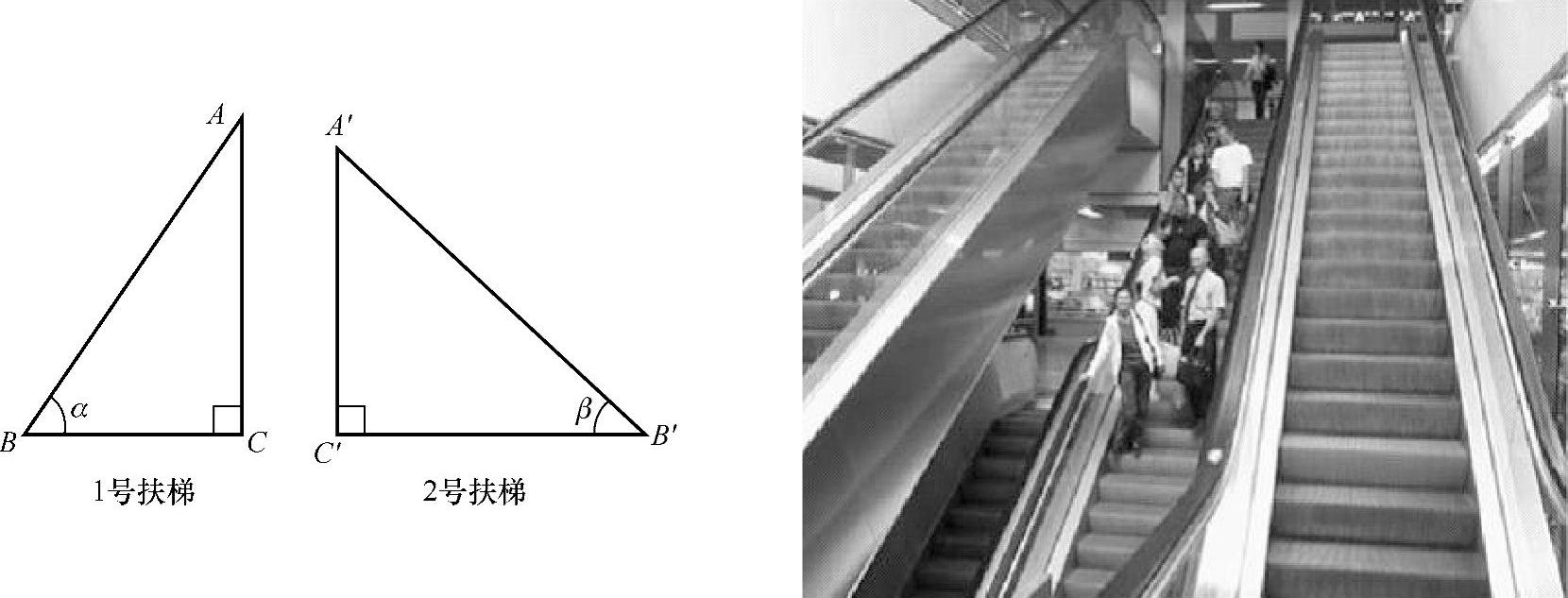
978-7-111-45466-3-Chapter02-24.jpg

图2-5

∠A的对边与邻边的比叫做∠A的正弦（sine），记作sinA，即978-7-111-45466-3-Chapter02-25.jpg

∠A的邻边与斜边的比叫做∠A的余弦（cosine），记作

cosA，即978-7-111-45466-3-Chapter02-26.jpg

∠A的对边与∠A的邻边的比叫做∠A的正切（tangent），

记作tanA，即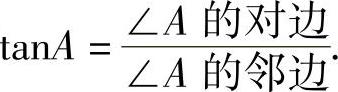978-7-111-45466-3-Chapter02-27.jpg

∠A的正弦、余弦和正切统称∠A的三角函数.

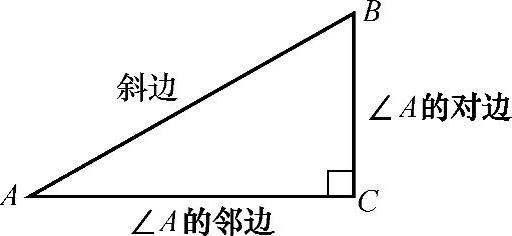
978-7-111-45466-3-Chapter02-28.jpg

图2-6

注意：sinA，cosA，tanA都是一个完整的符号，单独的“sin”没有意义，其中A前面的“∠”一般可以省略不写.

例1　如图2-7所示，在Rt△ABC中，∠C=90°，AB=5，BC=3，分别求∠A和∠B的正弦、余弦、正切.

分析：由勾股定理求出AC的长度，再根据直角三角形中锐角三角函数值与三边之间的关系求出各函数值.

解：由勾股定理知，AC2=AB2-BC2=52-32=16，

所以AC=4.

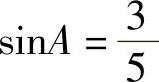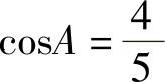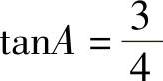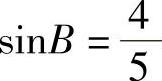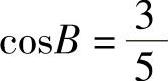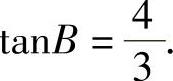
因此978-7-111-45466-3-Chapter02-29.jpg，978-7-111-45466-3-Chapter02-30.jpg，978-7-111-45466-3-Chapter02-31.jpg，978-7-111-45466-3-Chapter02-32.jpg，978-7-111-45466-3-Chapter02-33.jpg，978-7-111-45466-3-Chapter02-34.jpg

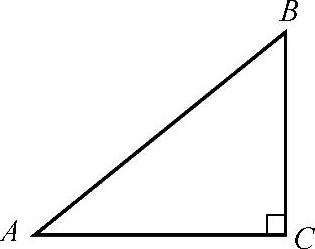
978-7-111-45466-3-Chapter02-35.jpg

图2-7

想一想

在直角三角形中，∠C=90°，sinA与cosB有什么关系？

练习

1.在等腰三角形ABC中，AB=AC=5，BC=6，求sinB，cosB，tanB.

2.在△ABC中，∠C=90°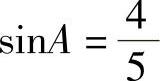，978-7-111-45466-3-Chapter02-36.jpg，BC=20，求△ABC的周长.

试一试

两块不同的三角尺中有几个不同的锐角？分别是多少度？你能分别求出这几个锐角的正弦值、余弦值和正切值吗？

通过计算，我们可以得到如下结论（见表2-3）.

表2-3

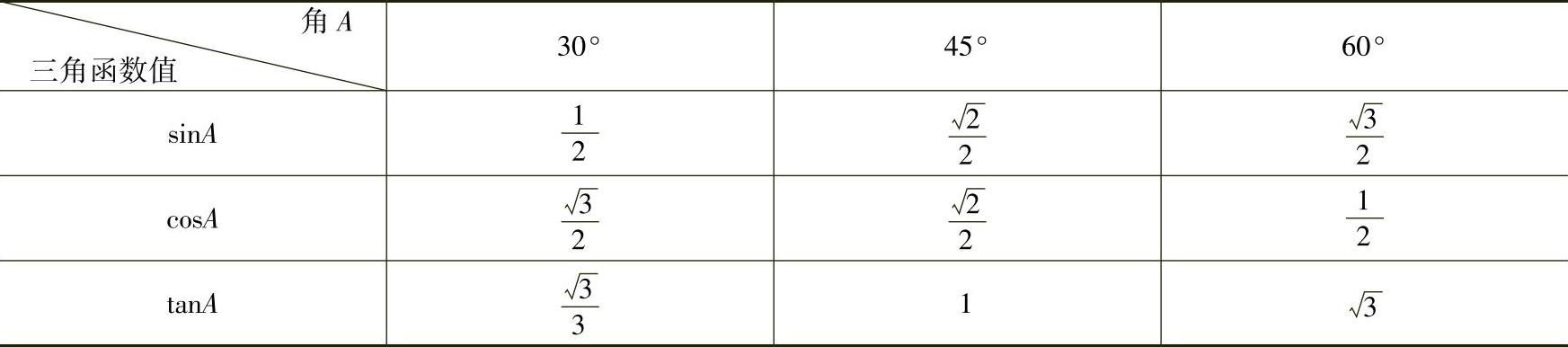
978-7-111-45466-3-Chapter02-37.jpg

例2　计算：

（1）sin30°+cos45°；

（2）sin260°+cos260°-tan45°；

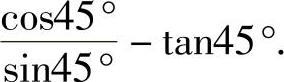
（3）978-7-111-45466-3-Chapter02-38.jpg

解：（1）原式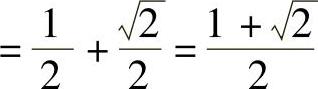978-7-111-45466-3-Chapter02-39.jpg；

（2）原式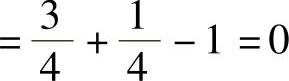978-7-111-45466-3-Chapter02-40.jpg；

（3）原式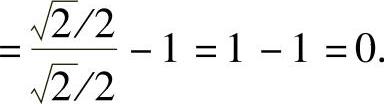978-7-111-45466-3-Chapter02-41.jpg

练习

1.计算：(www.chuimin.cn)

（1）tan45°-sin30°；

（2）cos60°+sin45°-tan30°；

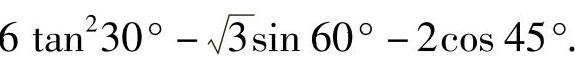
（3）978-7-111-45466-3-Chapter02-42.jpg

2.如习题图2-3所示，SO是等腰三角形SAB的高，已知∠ASB=120°，AB=54，求SO的长.

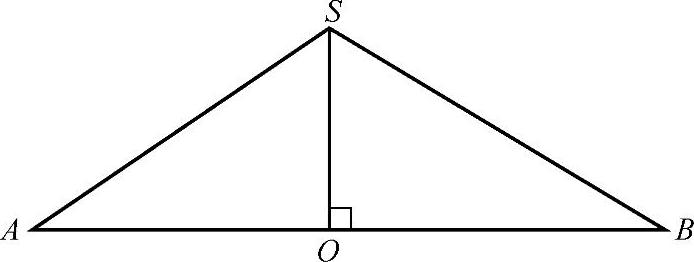
978-7-111-45466-3-Chapter02-43.jpg

习题图2-3

例3　图2-8是某机器零件的图形，求点B的坐标.

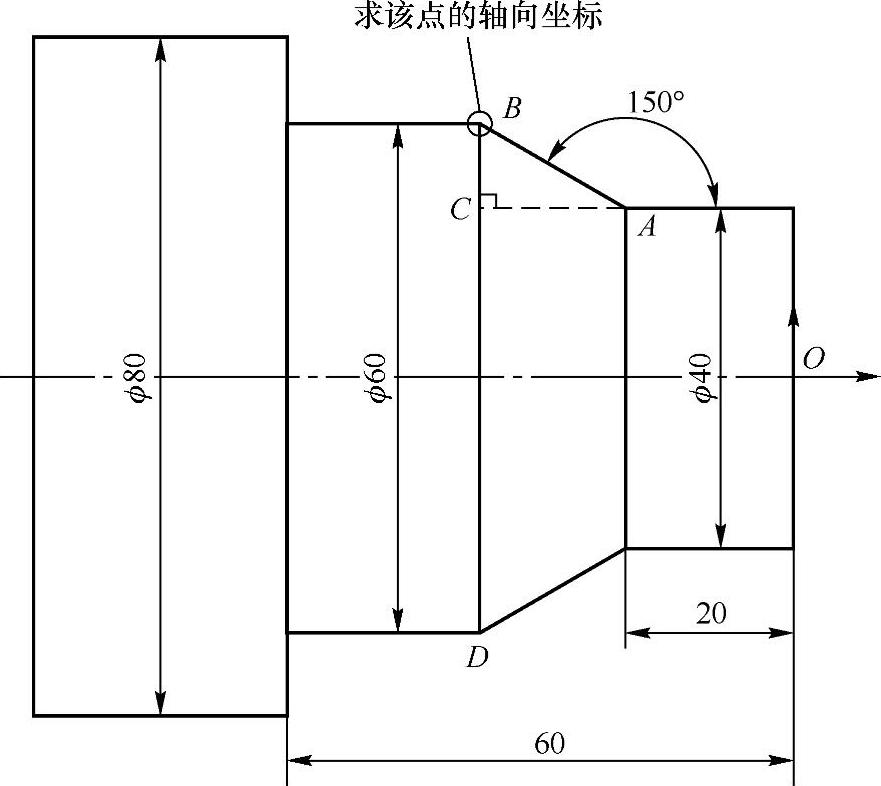
978-7-111-45466-3-Chapter02-44.jpg

图2-8

解：过点A作AC垂直于点B所在的直线BD，垂足为C.

由图2-8可知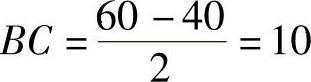978-7-111-45466-3-Chapter02-45.jpg

（ϕ60，ϕ40为圆的直径）.

因此在直角三角形ABC中，∠BAC=180°-150°=30°.

因为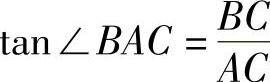978-7-111-45466-3-Chapter02-46.jpg，

所以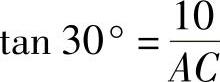978-7-111-45466-3-Chapter02-47.jpg，

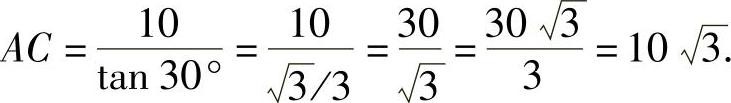
978-7-111-45466-3-Chapter02-48.jpg

故点B的横坐标为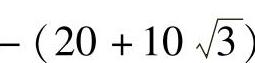978-7-111-45466-3-Chapter02-49.jpg，纵坐标为30.

习题二

1.填空题.

（1）如习题图2-4所示，在Rt△ABC中，∠C=90°.

978-7-111-45466-3-Chapter02-50.jpg

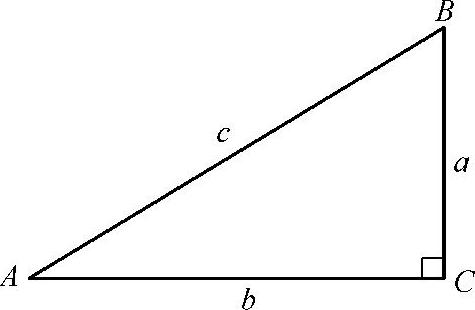
978-7-111-45466-3-Chapter02-51.jpg

习题图2-4

（2）在Rt△ABC中，∠C=90°，若a=9，b=12，则c=，

sinA=，cosA=，tanA=，

sinB=，cosB=，tanB=.

（3）在Rt△ABC中，∠C=90°，若∠A=30°，则∠B=，

sinA=，cosA=，tanA=，

sinB=，cosB=，tanB=.

（4）在Rt△ABC中，∠C=90°，已知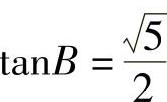978-7-111-45466-3-Chapter02-52.jpg，则cosA=.

2.选择题.

（1）已知：Rt△ABC中，∠C=90°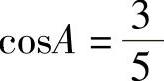，978-7-111-45466-3-Chapter02-53.jpg，AB=15，则AC的长是（ ）.

A.3 B.6 C.9 D.12

（2）下列各式中不正确的是（ ）.

A.sin260°+cos260°=1 B.sin30°+cos30°=1

C.sin35°=cos55°D.tan45°>sin45°

（3）计算2sin30°-2cos60°+tan45°的结果是（ ）.

978-7-111-45466-3-Chapter02-54.jpg

（4）在△ABC中，三边之比为a∶b∶c=1∶3∶2，则sinA+tanA等于（ ）.

978-7-111-45466-3-Chapter02-55.jpg

3.解答题.

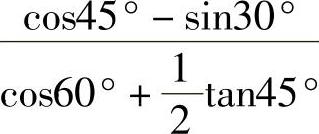（1）计算978-7-111-45466-3-Chapter02-56.jpg的值.

（2）已知，等腰△ABC的腰长为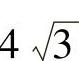978-7-111-45466-3-Chapter02-57.jpg，底角为30°，求三角形底边上的高和周长.

（3）已知Rt△ABC中，∠C=90°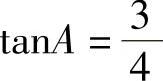，978-7-111-45466-3-Chapter02-58.jpg，BC=12，求AC，AB和cosB.

有关机电应用数学的文章

  • 任意角三角函数|机电应用数学 任意角三角函数|机电应用数学

    1.任意角的三角函数的定义在本章的2.2节已经讨论了锐角的三角函数值，但是把角的概念推广以后，角可以为任意大小，那么对于任意角α，又该如何确定其三角函数值呢？......

    2023-11-22

    详细阅读
  • 投影现象及其应用-机电应用数学 投影现象及其应用-机电应用数学

    我们知道，光是沿直线传播的.物体在光线的照射下，会在不透明物体后面的屏幕上（如墙面或地面等）留下这个物体的影子（见图3-39），这种现象就叫做投影.其中，把光线叫做投影线，把留下物体影子的屏幕叫做投影面.图3-39（1）中心投影把光由一点向外散射所形成的投影，叫做中心投影（见图3-40）.中心投影的投影线交于一点，即投射中心.中心投影现象普遍存在于我们的生活中.例如，舞台灯、路灯、手电筒和台灯的光......

    2023-11-22

    详细阅读
  • 正弦函数性质及解析-机电应用数学 正弦函数性质及解析-机电应用数学

    由正弦函数y=sinx的图像可知：定义域正弦函数y=sinx的定义域是R.值域正弦函数y=sinx，x∈R的值域是[-1，1]，即对任意的x∈R，都有-1≤sinx≤1.其中，当，k∈Z，有ymax=1；当，k∈Z时，有ymin=-1.想一想等式2sinx=3，，都成立吗？例2求出下列函数的最大值和最小值：y=1-sinx； y=2sinx.解：当sinx=-1时，ymax=1-（-1）=2；当sinx=1时，ymin=1-1=0.当sinx=1时，ymax=2×1=2；sinx=-1时，ymin=2×（-1）=-2.想一想第题中的函数y=1-sinx取得最大值和最小值时，对应的x的取值集合分别是什么？......

    2023-11-22

    详细阅读
  • 机电应用数学：任意点的空间坐标表达 机电应用数学：任意点的空间坐标表达

    建立了空间直角坐标系以后，空间中任意一点M应如何用坐标表示呢？......

    2023-11-22

    详细阅读
  • 理解圆形的方程表示-机电应用数学 理解圆形的方程表示-机电应用数学

    观察与思考我们已经初步体会了用方程研究直线的便利和用直线反映相关方程的直观，那么其他曲线是否也可以建立与某一类方程之间的关系呢？......

    2023-11-22

    详细阅读
  • 三角函数的应用举例，探索28.6 三角函数的应用举例，探索28.6

    1．直角梯形ABCD如图放置，AB，CD为水平线，BC⊥AB，如果∠BCA＝67°，从低处A看高处C，那么点C在点A的（ ）．A．俯角67°方向 B．俯角23°方向C．仰角67°方向 D．仰角23°方向（第1题）（第2题）2．如图，在桥外一点A测得大桥主架与水面的交汇点C的俯角为α，大桥主架的顶端D的仰角为β，已知测量点与大桥主架的水平距离AB＝a，则此时大桥主架顶端离水面的高CD为（ ）．3．如......

    2023-07-03

    详细阅读
  • 机电应用数学：椭圆的标准方程与定义 机电应用数学：椭圆的标准方程与定义

    1.椭圆的定义做一做取一条一定长的细绳，把它的两端固定在画图板上的F1和F2两点，当绳长大于F1和F2的距离时，用铅笔尖把绳子拉紧，使笔尖在图板上慢慢移动，请同学们利用手中绳子配合同桌共同完成，看看可以得到什么图形.图4-18议一议在画图的过程中，哪些量发生了变化？......

    2023-11-22

    详细阅读
  • 机电应用数学：解析幂的运算方法 机电应用数学：解析幂的运算方法

    在初中我们学习了正整数指数，我们知道a2=a·aa3=a·a·aan=a·a·…......

    2023-11-22

    详细阅读