【摘要】:请你为剩下的那个图像写出与之相吻合的事件.习题图2-2我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;我骑着车一路匀速行驶,只是在途中遇到了一次交通堵塞,耽搁了一些时间;我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
观察与思考
问题(1):汽车以60km/h的速度匀速行驶,行驶里程为s(km),行驶时间为t(h),先填写下表,再试用含有t的式子表示s.

观察填出的表格,你会发现:在这个变化过程中,s是随着t的变化而变化的,每当行驶时间t取定一个值时,行驶里程s就随之确定一个值.
问题(2):小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按16元/h计算.设小明的哥哥这个月工作的时间为t(h),应得报酬为m(元),填写下表.

观察表格:在这个变化过程中,有两个变量,对每一个确定的值,都有唯一确定的值与它对应.那你能找出哪个变量随哪个变量变化吗?
一般地,在一个变化过程中有两个变量x与y,如果对于每一个x都有唯一确定的值y与它对应,那么就说y是x的函数,x叫自变量,y的取值叫做函数值.
例如,在问题(1)中,当自变量t=1(h)时,所对应的函数值是s=60(km);t=2(h)时,函数值是s=120(km).
另外,函数关系实质上是表现为两个变量之间的一种对应关系,如果我们用f来表示这种对应关系,那么函数也可以表示成y=f(x)的形式.
例如,函数y=2x+1,也可以表示成f(x)=2x+1;函数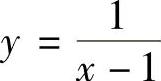 ,也可以表示成
,也可以表示成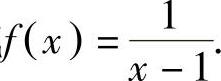
在初中阶段我们已经学习过一次函数、二次函数和反比例函数,现在简单回顾一下它们的图像和性质.
1.一次函数
一次函数解析式为y=kx+b(k≠0),图像为一条直线,特别地,当b=0时,解析式变为y=kx,即为正比例函数,因此正比例函数是一种特殊的一次函数.
例1 作出一次函数y=2x+1和y=-2x+5的图像.
解:列表如下.

描点并连线.
由图2-1可知,y=2x+1的图像是从左向右逐渐上升的,即y随x的增大而增大,此时我们称这个函数在给定范围内为增函数;y=-2x+5的图像是从左向右逐渐下降的,即y随x的增大而减小,此时我们称这个函数在给定范围内为减函数.
函数y=f(x)在某个范围内单调递增或单调递减的性质,叫做函数的单调性.
因此,我们可以得出结论:一次函数当k>0时,函数单调性为增函数;当k<0时,函数单调性为减函数
练一练
作出下列一次函数图像:
(1)y=4x-2; (2)y=-x-1.
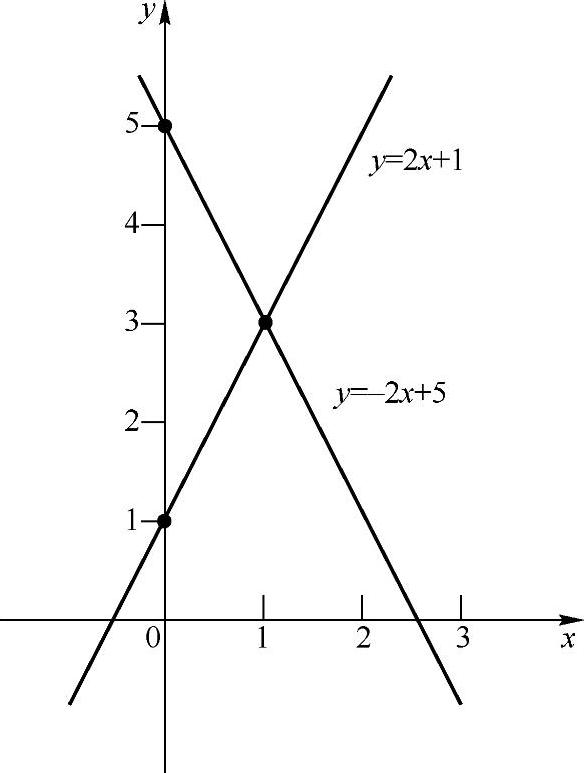
图2-1
2.二次函数
二次函数的解析式为y=ax2+bx+c(a≠0),其图像为抛物线,具体图像如表2-1所示.
表2-1 二次函数的图像及其性质
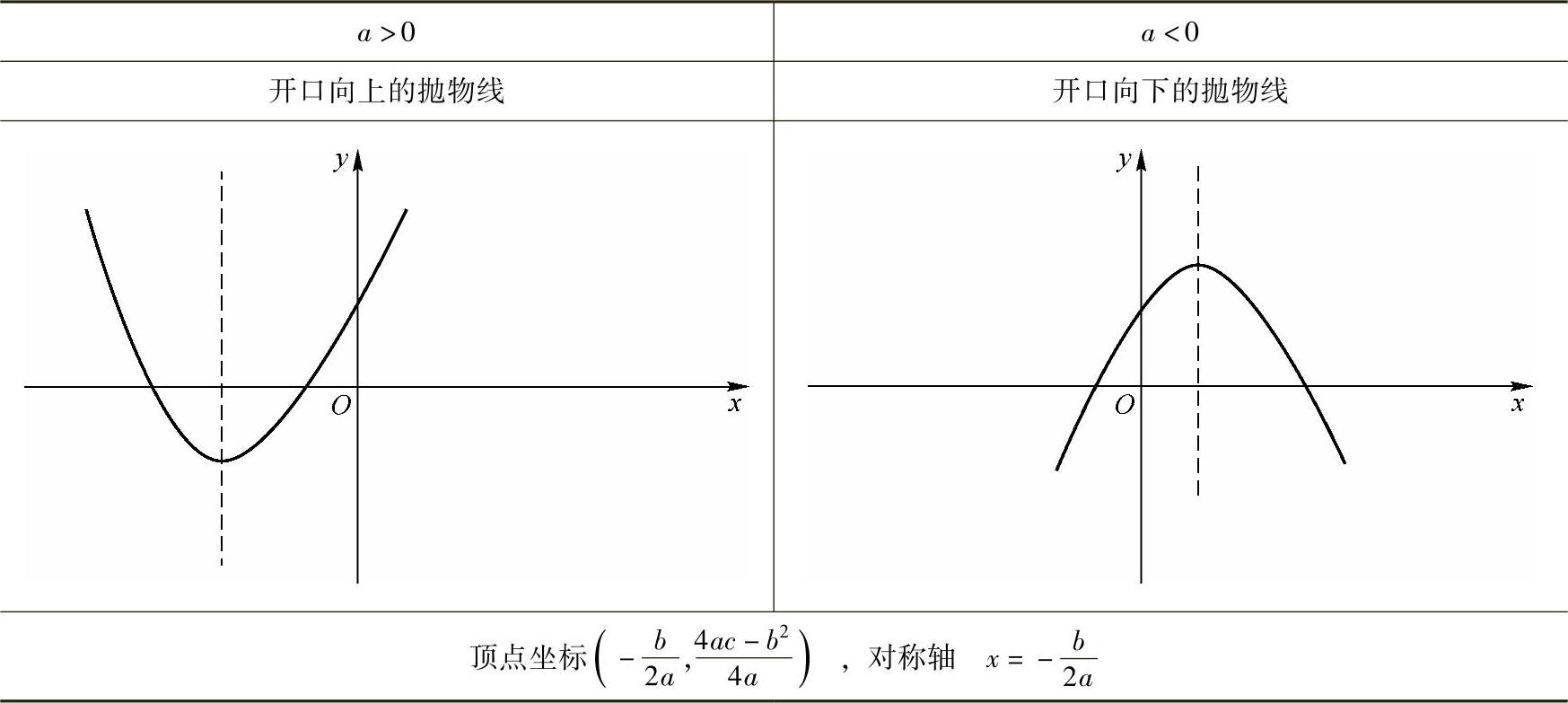
例2 确定下列二次函数图像的开口方向、对称轴和顶点坐标,作出草图,并讨论它们的单调性:
(1)y=-2x2;(2)y=3x2-6x+2.
解:(1)由于a=-2<0,所以抛物线开口向下,对称轴为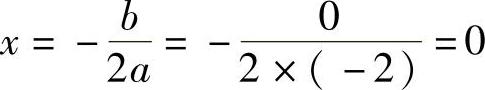 ,即为y轴,
,即为y轴,
顶点坐标:横坐标x=0,
纵坐标 ,
,
所以顶点坐标为(0,0).
由图2-2a可知,当x<0时,函数为增函数;
当x>0时,函数为减函数.
(2)由于a=3>0,所以抛物线开口向上,对称轴为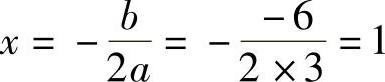 ,
,
顶点坐标:横坐标x=1,
纵坐标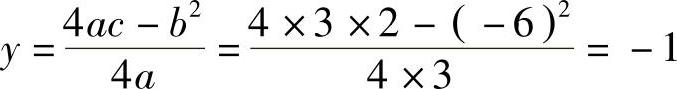 ,
,
所以顶点坐标为(1,-1).
由图2-2b可知,当x<1时,函数为减函数;
当x>1时,函数为增函数.
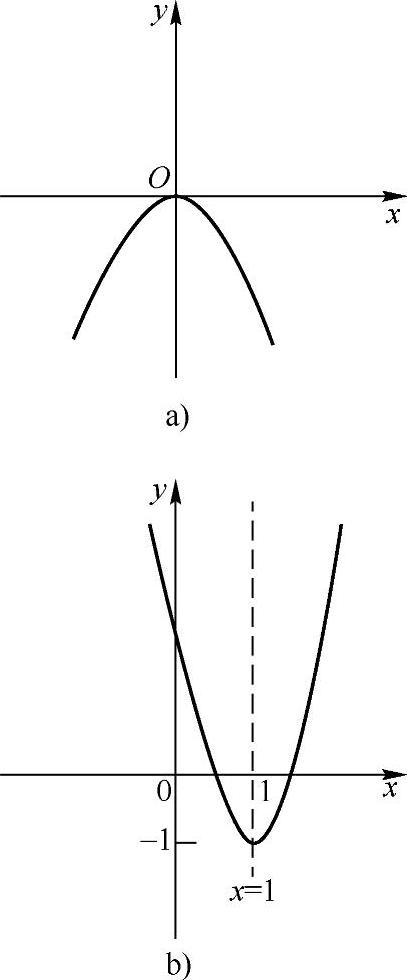
图2-2(www.chuimin.cn)
练习
作出下列二次函数的草图,并判断单调性:
(1)y=1+2x-x2; (2)y=x2+6x+9.
3.反比例函数
反比例函数的解析式为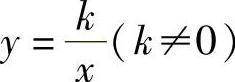
,其图像为双曲线,具体图像如表2-2所示.
表2-2 反比例函数的图像及其性质
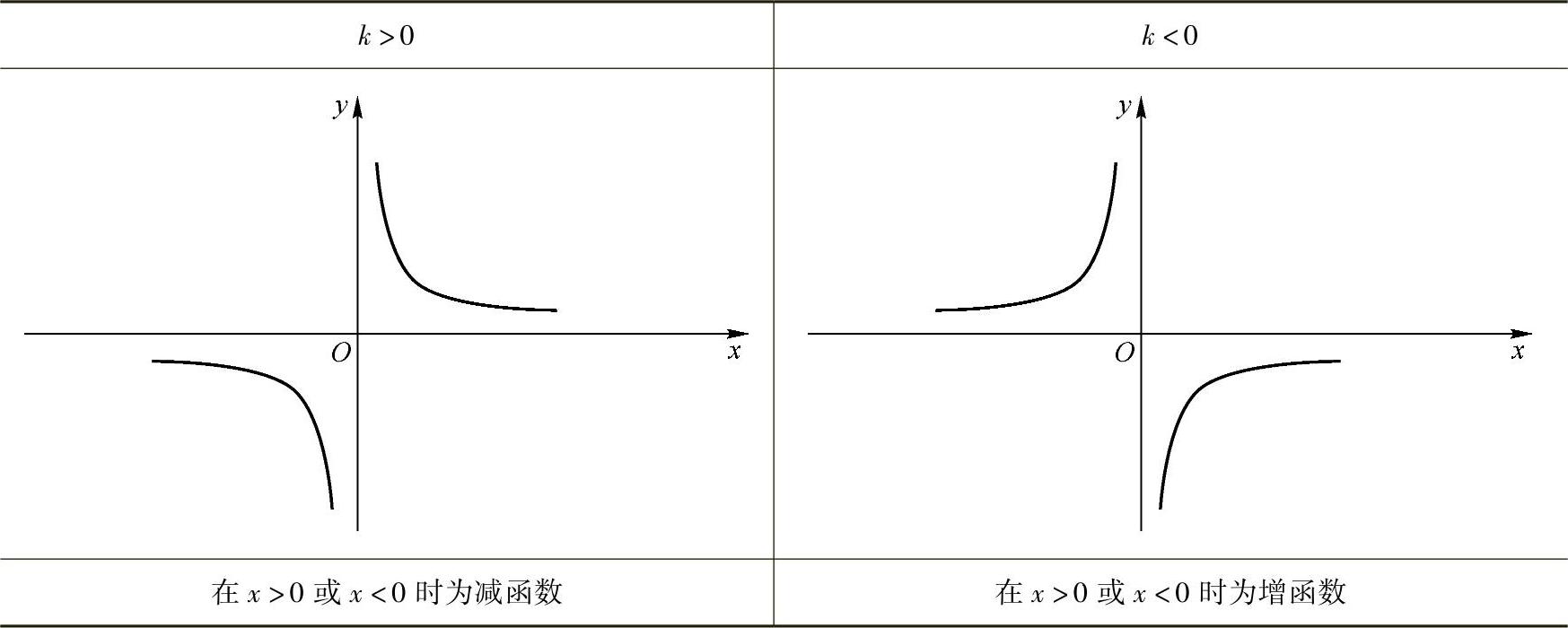
另外,通过以上几种初等函数的图像我们看到:有些图像是关于y轴对称的;有些图像是关于原点对称的.若一个函数图像关于y轴对称,我们称这个函数为偶函数,比如函数
y=-2x2,即为偶函数;若图像关于原点对称,我们称这个函数为奇函数,比如反比例函数,即为奇函数.
例3 作出函数y=x的图像,并判断它的奇偶性.
解:由函数解析式可知,函数值y≥0,
并且当x≥0时,函数为y=x;当x≤0时,函数为y=-x
分别列表如下:


描点并连线.
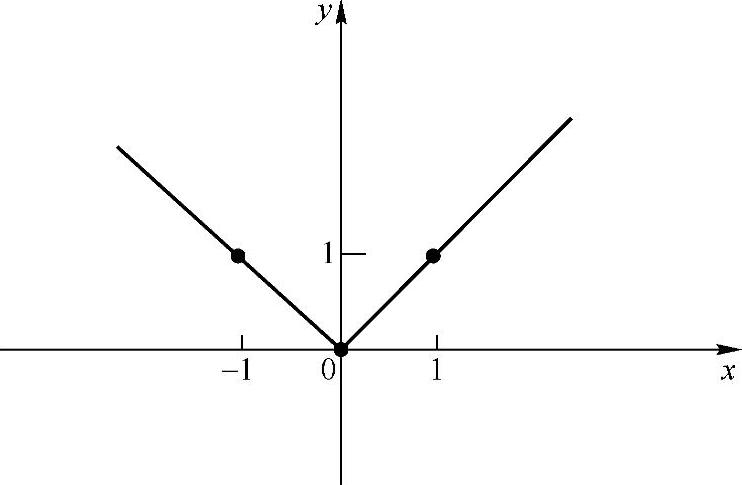
图2-3
由图2-3可知,函数图像关于y轴对称,所以函数为偶函数.
练习
1.填空题.
(1)f(3)=8表示当=3时,=8;
(2)函数y=-x2在[0,4]上的单调性为,在[-4,0]上的单调性为.
2.写出下列函数关系式:
(1)英华文化用品商店库存某种品牌的计算器150台,每台售价45元,求销售额y(元)与销售量x(台)之间的函数关系式;
(2)用一块矩形空地做花圃,这块地长30m,宽25m,如在四周留出宽度是xm的小路,中间余下种花的空地面积为ym2,求y与x之间的函数关系式;
(3)加工一批零件,先用15min做准备工作,然后每加工一个零件用10min,写出零件个数y和工作时间x(min)之间的函数关系式.
习题一
1.已知函数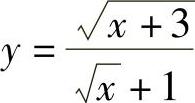 ,求x=0,x=1,x=4时分别对应的函数值.
,求x=0,x=1,x=4时分别对应的函数值.
2.已知函数f(x)=2x2-3x-4,填写下表:

3.画出下列函数的图像,并根据图像判断其单调性和奇偶性.
(1)y=2x;(2)y=-2x+1;(3)y=x2+2;
(4)y=1+2x-x2;
(5)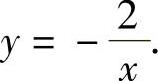
4.习题图2-1a、b分别给出了奇函数f(x)和偶函数g(x)的部分图像,请画出函数的剩余图像,并说明理由.
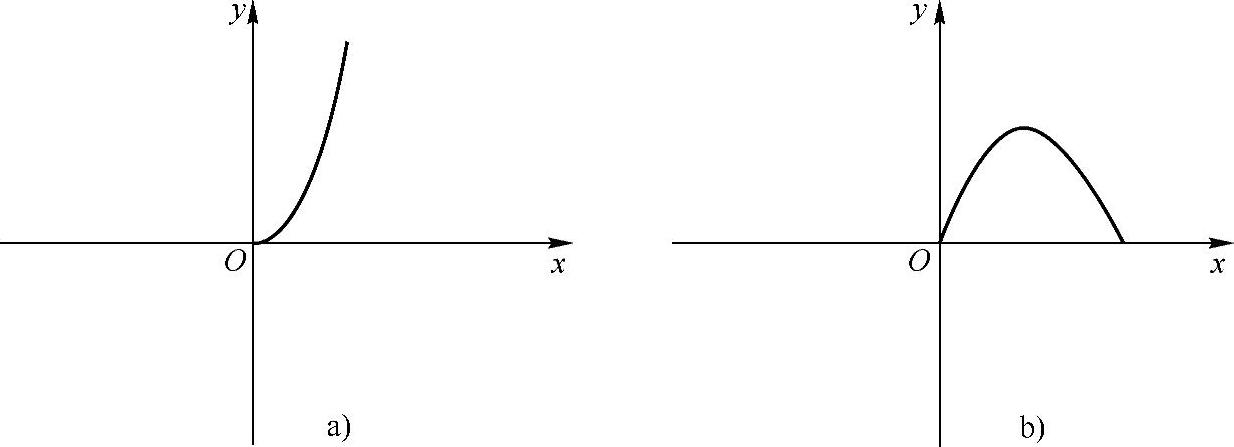
习题图2-1
5.习题图2-2a~d中哪几个图像与下述三件事分别吻合得最好?请你为剩下的那个图像写出与之相吻合的事件.
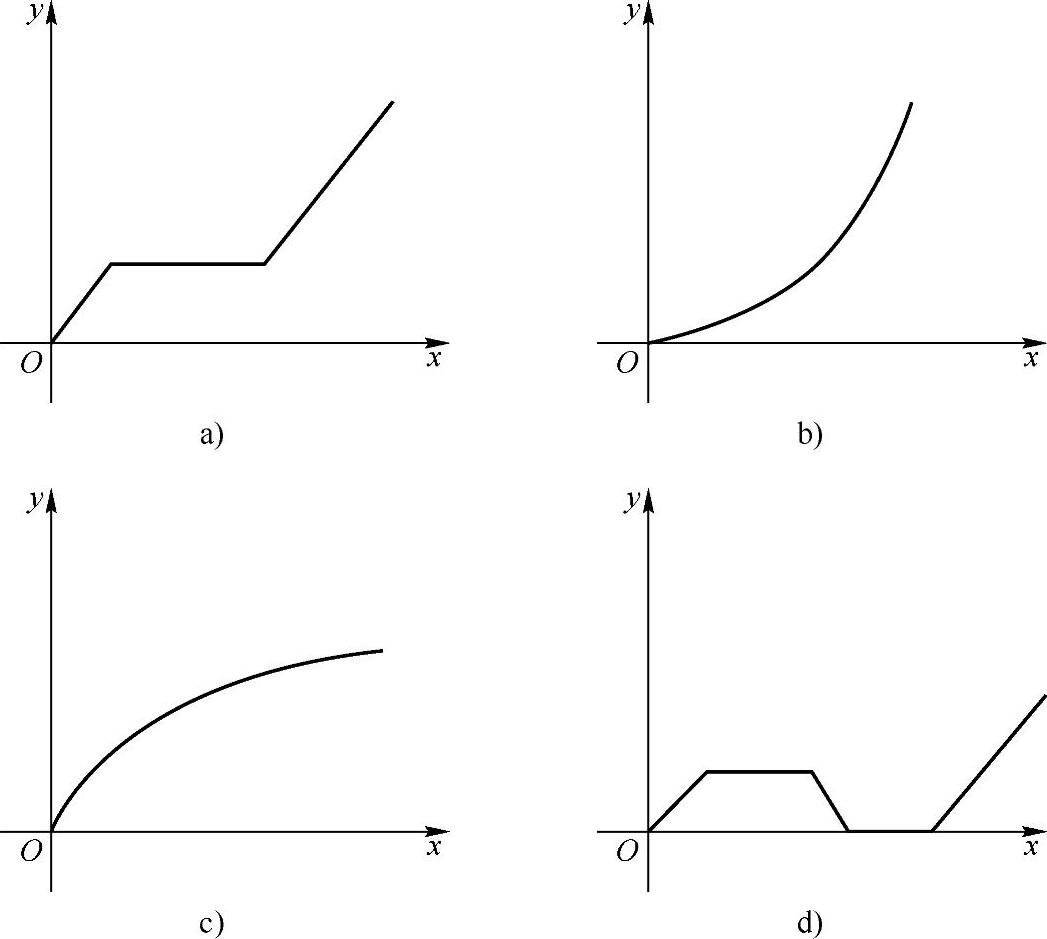
习题图2-2
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车一路匀速行驶,只是在途中遇到了一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.



 ,也可以表示成
,也可以表示成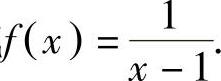



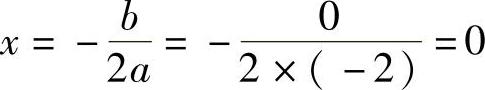 ,即为
,即为 ,
,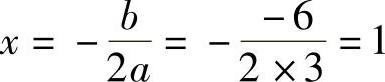 ,
,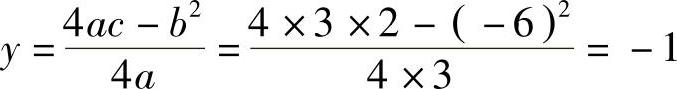 ,
,
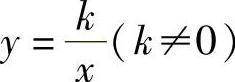




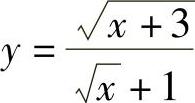 ,求
,求
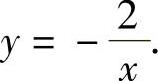







相关推荐