请说明理由．若矩形ABCD面积为6，求四边形BDEG的面积．（第9题）10．在如图所示的平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2A3B3与△B2A2B1关于点B2成中心对称……......
2023-07-03
求解问题：矩形画面如何镶嵌彩纸
【摘要】：引例某校团委准备举办学生绘画展览，为美化画面，在长30cm、宽20cm的矩形画面四周镶上宽度相等的彩纸，并使彩纸的面积恰好与原面积相等.想一想彩纸的宽度是多少？
引例
某校团委准备举办学生绘画展览，为美化画面，在长30cm、宽20cm的矩形画面四周镶上宽度相等的彩纸，并使彩纸的面积恰好与原面积相等.
想一想
彩纸的宽度是多少？
1.一元二次方程的定义
只含有一个未知数，且未知数的最高次数是2的整式方程叫做一元二次方程，一元二次方程通常可化成如下的一般形式：
ax2+bx+c=0（a≠0）.
其中，a，b，c是已知数（a≠0），我们把a，b，c分别叫做二次项系数、一次项系数和常数项.
2.一元二次方程的一般解法
（1）直接开平方法
直接开平方法就是用直接开平方求解一元二次方程的方法.用直接开平方法解形如（x-m）2=n（n≥0）的方程.
例1 用直接开平方法解下列一元二次方程：
（1）（3x+1）2=9； （2）（3x-2）2=（x+4）2；
（3）9x2-24x+16=121； （4）（3x+2）（3x-2）=4.
解：（1）由（3x+1）2=9得
3x+1=±3（注意不要丢解）
由3x+1=3得
，
由3x+1=-3得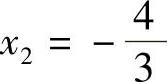
，
所以原方程的解为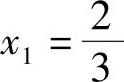
，
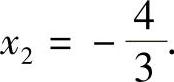
（2）由（3x-2）2=（x+4）2得
3x-2=x+4或3x-2=-（x+4）
由3x-2=x+4得x1=3，
由3x-2=-（x+4）得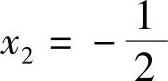
，
所以原方程的解为x1=3，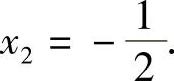
（3）由9x2-24x+16=121得
（3x-4）2=121
由3x-4=±11，
得x1=5，
，
所以原方程的解为x1=5，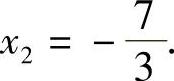
（4）由（3x+2）（3x-2）=4得
9x2-4=4，即9x2=8
由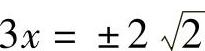
，
得
，
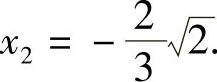
所以原方程的解为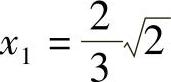
，
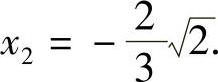
（2）配方法
用配方法解方程ax2+bx+c=0（a≠0），应先将常数c移到方程右边，再将二次项系数化为1，变为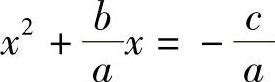
的形式.
例2 用配方法解下列一元二次方程：
（1）2x2-4x-2=0； （2）3x2-4x-2=0.
解：（1）2x2-4x-2=0
二次项系数化为1，移常数项得：x2-2x=1，
配方得：x2-2x+12=1+12，即（x-1）2=2，
直接开平方得：
，
，
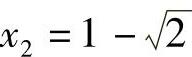
所以原方程的解为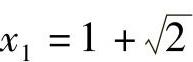
，
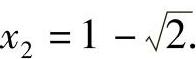
（2）3x2-4x-2=0
二次项系数化为1，移常数项得：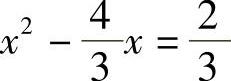
，
方程两边都加上一次项系数一半的平方得：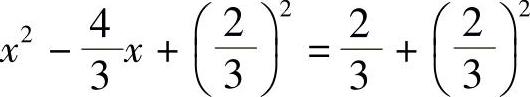
，
即
直接开平方得：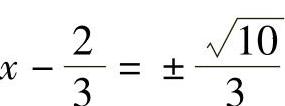
，即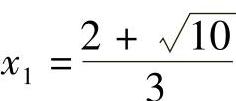
，
，
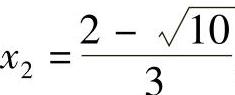所以原方程的解为
，
说明：配方法是一种基本的变形，解题中虽不常用，但作为一种基本方法要熟练掌握.
配方时应按下面的步骤进行：
先把二次项系数化为1，并把常数项移到等式的另一边；
再在方程两边同时加上一次项系数一半的平方；
最后变为完全平方式利用直接开平方法即可完成解题任务.
（3）公式法
用公式法就是指利用求根公式
，使用时应先把一元二次方程化成一般形式ax2+bx+c=0（a≠0），然后计算判别式b2-4ac的值，当b2-4≥0时，把各项系数的值代入求根公式即可得到方程的根.但要注意当b2-4ac<0时，方程无实数解.
例3 用公式法解下列方程.
（1）3x2+4=7x；
（2）
解：（1）将3x2+4=7x化为一般式(www.chuimin.cn)
3x2-7x+4=0
求出判别式的值：Δ=b2-4ac=1>0.
代入求根公式：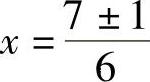
，
所以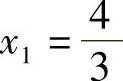
，x2=1.
（2）将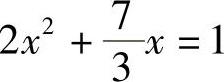
化为一般式
6x2+7x-3=0
求出判别式的值：Δ=b2-4ac=49+72=121>0.
代入求根公式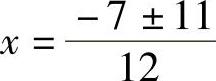
，
所以
，
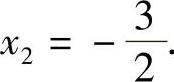
说明：公式法可以用于解任何一元二次方程，在找不到简单方法时，即考虑化为一般形式后使用公式法.但在应用公式法时要先明确公式中的字母在题目中所表示的量，再求出判别式的值，解得的根还要进行化简.
（4）分解因式法
分解因式法是把方程一边变形为零，把另一边的二次三项式分解成两个一次因式的积的形式.
例4 用分解因式法解下列方程：
（1）6x2+x-15=0； （2）（x+3）（x-6）=-8.
解：（1）将6x2+x-15=0左边分解成两个因式的积得：（2x-3）（3x+5）=0，
于是可得：2x-3=0，3x+5=0，
（2）将（x+3）（x-6）=-8化简为一般式得：
x2-3x-10=0
左边分解成两个因式的积得：（x+2）（x-5）=0，
于是可得：
所以x1=-2，x2=5.
练习
1.用直接开平方法解下列方程：
（1）x2=8；（2）3（x-3）2=0；
（3）x2-4x+3=0；（4）4（1-x）2-9=0.
2.用配方法解下列方程：
（1）x2-4x-1=0；
（2）
；
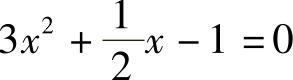（3）3x2-4x-7=0；（4）2x2-18=3x.
3.用公式法解下列方程：
4.用因式分解法解下列方程：
（1）（x+1）2-2=0；（2）（x+2）2=2x+4；
（3）x2=6x；（4）2x2-9x-18=0.
5.选用适当的方法解下列方程：
（1）（x+1）（6x-5）=0；（2）
；
（3）2（x+5）2=x（x+5）；（4）x2-5x+2=0.
6.已知a-1=2，解关于x的方程（a-9）x2-4ax+1=5x-2ax2-2.
7.有一个两位数等于其数字之积的3倍，其十位数字比个位数字小2，求这两位数.
习题七
1.用直接开平方法解下列方程：
（1）x2-2=23；（2）4（x+5）2=28；
（3）x2-2x-3=0；（4）4（2+x）2-25=0.
2.用配方法解下列方程：
（1）x2-3x+1=0；（2）2x2+6=7x；
（3）3x2-9x+2=0.
3.用公式法解下列方程：
（1）2x2-9x+8=0；（2）9x2+6x+1=0；
（3）16x2+8x=3.
4.用因式分解法解下列方程：
（1）（4x-1）（5x+7）=0；（2）3x（x-1）=2-2x；
（3）（2x+3）2=4（2x+3）.
5.选用适当的方法解下列方程：
（1）（2x+1）2-3（2x+1）+2=0；（2）（2x-3）x-4（2x-3）=9；
（3）
；
（4）（2x+1）2=2（2x+1）.
6.有一个两位数，它们的十位数字与个位数字之和为8，如果把十位数字与个位数字调换后，所得的两位数乘以原来的两位数就得1855，求原来的两位数.
7.要做一个高是8cm，底面的长比宽多5cm，体积是528cm3的长方体木箱，问底面的长和宽各是多少？
有关机电应用数学的文章
- 详细阅读
-
使用节点电压法求解电路问题详细阅读
引入节点电压法的目的和引入回路电流法的目的相同，都是为了简化分析和计算电路的步骤。以图2.5所示电路为例，具体说明节点电压法的适用范围及其解题步骤。在图2.3中标示的各支路电流的参考方向下，根据欧姆定律可得图2.5节点电压法电路举例显然，只要求出各节点电位，由上述关系即可求出各支路电流。由于这种解题形式是以节点电压为未知量，进而对电路进行分析计算的方法，因而称为节点电压法。建立求解节点电压的KCL方程。......
2023-06-24
-
使用特尔菲法求解问题详细阅读
特尔菲法又称专家调查法，是20世纪50年代初由美国兰德公司创立的预测方法。对预测结果进行分析和评价是特尔菲法最后阶段的工作，也是最重要的工作。表9.1专家预测成果统计表试用特尔菲法，对该灌区非农业用地增长百分数做出预测。表9.2专家预测值及权重值解:=15%×+12%×+10%×+8%×+4%×=290.5%=1.5+1.0+2.0+1.5+1.0×2+2.5+2.0+1.5×2+1.0+2.5+2.0×2+1.5×2+1.0+2.5+1.0×2=31.5用加权平均法求得该区明年的非农业用地增长百分数为9.22%。......
2023-06-30
-
如何求解能力统计量？详细阅读
能力验证结果通常需要转化为能力统计量，以便进行解释和与其他确定的目标作比较。其目的是依据能力评定准则来度量与指定值的偏离。能力统计量也成为性能统计量。根据《CNAS－GL002：2018能力验证结果的统计处理和能力评价指南》，按照对参加者结果转化由简至繁的顺序，定量结果的常用统计量包括以下六种。需要特别注意的是，应尽量不使用多个能力比分数的平均值作为参加者的能力统计量。......
2023-06-29
-
多目标问题求解方法大揭秘详细阅读
权重和法可表示为权重可以看作决策者对于目标函数的偏好，即多目标之间的相对重要性。在实际应用中，往往准确的权重或各目标之间优先级很难获得，如果无法获得对目标函数的先验偏好信息，就只能采用产生式方法来求解问题以获得Pareto最优解集。由于产生式方法在优化过程中产生了较多的Pareto最优解，在处理高维目标优化问题时，其选择无法直接表明，导致计算代价过大。图9-3多目标优化求解策略示意......
2023-07-02
-
遗传算法优化问题求解详细阅读
遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。遗传算法之所以具备强大的搜索能力，是因为包罗了选择、杂交和变异三种基本操作算子，同时这三种操作算子也是模拟自然生物圈中自然存在的有性繁殖、杂交和变异等现象的核心载体。同样，遗传算法中起核心作用的是遗传操作的交叉算子。通过交叉，遗传算法的搜索能力得以飞跃提高。图11-1遗传算法流程图......
2023-06-28
-
如何使用矩形命令RECTANG进行绘制详细阅读
执行RECTANG命令可采用以下三种方式：● 绘图工具栏 。启动绘矩形命令后,只需先后确定矩形的两个对角点便可绘出矩形。现将命令行提示的有关绘矩形方式的选项介绍如下：命令：_rectang指定第一个角点或 [倒角/标高/圆角/厚度/宽度]：0,0↙指定另一个角点或 [面积/尺寸/旋转]：420,297↙倒角：以设定的距离来做矩形的倒角。 常用画矩形命令举例。4）启动绘矩形命令。......
2023-06-21
-
用辅助平面法求解问题的方法和技巧详细阅读
为了方便、准确地作图，可选正平面为辅助面。当内表面由立体上的孔洞等结构形成时，内表面的相贯线画法与外表面的相贯线画法相同，只是其可见性要根据具体情况正确处理。图5-11两圆柱面正交的三种形式例5-3用辅助平面法求半球与圆柱体的截交线，如图5-12所示。根据积聚性可知，相贯线的俯视图积聚在圆柱体的圆周上，这时相贯线的正面投影要选辅助平面来求。图5-13相贯线的简化画法作图时注意，圆弧应向大圆柱体投影内弯曲。......
2023-06-28
相关推荐