首页理论教育机电应用数学：一次方程与二元方程组

机电应用数学：一次方程与二元方程组

2025-09-30 理论教育版权反馈

【摘要】：解：设绳长x尺，井深y尺，则式①-式②，得，即，则x=48，将x=48代入式①，得y=11，所以绳长48尺，井深11尺.练一练在图1-3中，当单刀双掷开关S扳到位置1时，外电路的电阻R1=14Ω，测得电流I1=0.2A；当S扳到位置2时，外电路电阻R2=9Ω，测得电流I2=0.3A，求电源的电动势E和内电阻r.工具箱E=RI+rI图1-3练习1.解下列方程：2=70+25x；；2.列方程解下列应用题.一件商品按成本价提高20%后标价，然后以9折销售，销售额为270元，这种商品的成本价是多少？

引例

一家商店将某种服装按成本价提高40%后标价，又以8折（即按标价的80%）优惠卖出，结果每件仍获利15元，这种服装每件的成本是多少元？

想一想

这15元的利润是怎么来的？

1.一元一次方程

在一个方程中，只含有一个未知数（元），并且未知数的指数是1（次），这样的方程叫做一元一次方程.

例1　解下列方程：

（1）2x+3=5；

（2）

解：（1）移项，得2x=5-3，合并同类项得2x=2，系数化成1，得x=1；

（2）移项，得，合并同类项，得，系数化成1，得x=-36.

例2　解下列方程：

（1）3x+3=2x+7；

（2）；

解：（1）移项，得3x-2x=7-3，合并同类项，得x=4；

（2）移项，得，合并同类项，得，系数化成1，得x=4.

例3　解方程：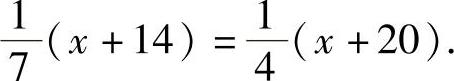

解：去分母，得4（x+14）=7（x+20），去括号，得4x+56=7x+140，移项，合并同类项，得-3x=84，系数化成1，得x=-28.

想一想

解一元一次方程有哪些步骤？

试一试

1.有一220V、40W的白炽灯，接在220V的供电线路上，若电价为0.42元/kW·h，每月（以30天计算）应付电费1.26元，求每天的用电量.

工具箱

P=UI

2.一个功率为1kW、电压U为220V的电炉，正常工作时电流I是多大？如果不考虑温度对电阻的影响，把它接在110V的电压上，它的功率P将是多少？

2.二元一次方程组

含有两个未知数，并且所含未知数的项的次数都是1的方程叫做二元一次方程.

含有两个未知数的两个一次方程所组成的一组方程，叫做二元一次方程组.二元一次方程组中各个方程的公共解，叫做这个二元一次方程组的解.

例4　解下列方程组.

解：（1）式①+式②，得-2x=16，即x=-8，将x=-8代入式①，得y=31，

原方程组的解是

（2）式②-式①×3，得2x=10，即x=5，将x=5代入式①，得y=3，

原方程组的解是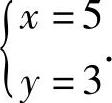(https://www.chuimin.cn)

例5　以绳测井，若将绳三折测之，绳多五尺；若将绳四折测之，绳多一尺.绳长、井深各几尺？

解：设绳长x尺，井深y尺，则

式①-式②，得，即，则x=48，

将x=48代入式①，得y=11，所以绳长48尺，井深11尺.

练一练

在图1-3中，当单刀双掷开关S扳到位置1时，外电路的电阻R₁=14Ω，测得电流I₁=0.2A；当S扳到位置2时，外电路电阻R₂=9Ω，测得电流I₂=0.3A，求电源的电动势E和内电阻r.

工具箱

E=RI+rI

图1-3

练习

1.解下列方程：

（1）2（200-15x）=70+25x；

（2）；

2.列方程解下列应用题.

（1）一件商品按成本价提高20%后标价，然后以9折销售，销售额为270元，这种商品的成本价是多少？

（2）某商场的电视机原价为2500元，现以8折销售，如果想使降价前后的销售额都为10万元，那么销售量应增加多少？

习题五

1.解下列方程：

2.解下列方程组：

3.列方程解下列应用题：

（1）在一卷公元前2025年左右遗留下来的古埃及草卷中，记载着一些数学问题，其中一个问题翻译过来是：“啊哈，它的全部，它的，其和等于19.”你能求出问题中的“它”吗？

（2）甲、乙两队开展足球对抗赛，规定每队胜一场得3分，平一场得1分，负一场得0分.甲队与乙队一共进行了10场比赛，甲队得了22分.甲队胜了多少场？平了多少场？

（3）有一些分别标有6，12，18，24，…的卡片，后一张卡片上的数比前一张卡片上的数大6，小朋拿到了相邻的3张卡片，且这些卡片上的数之和为342.

a.小朋拿到了哪3张卡片？

b.你能拿到相邻的3张卡片，使得这些卡片上的数之和是86吗？

（4）列方程组解下列应用题：

a.“今有牛五、羊二，值金十两.牛二，羊五，值金八两.牛，羊各值金几何？”

b.甲、乙两人从相距36km的两地相向而行.如果甲比乙先走2h，那么它们在乙出发2.5h后相遇；如果乙比甲先走2h，那么他们在甲出发3h后相遇.甲、乙两人每小时各走多少千米？