复数的连乘以及乘法规则

2023-11-22 理论教育版权反馈

【摘要】：例6计算：（2-i）.分析：多个复数连乘时，应该合理利用复数的乘法

引例

我们知道，在实数范围内，方程x²=2有两个解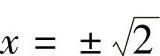，而方程x²=-1无解，即对于一元二次方程ax²+bx+c=0（a≠0），当b²-4ac<0时方程无解，我们无法利用求根公式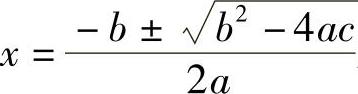来求得它的根.为了解决这个问题，人们将实数集进行了扩充，从而使方程x²=-1有解.

1.复数的有关概念

为了解决引例中的问题，人们引进了一个新数i，称为虚数单位，并规定：

（1）i²=-1；

（2）i与实数在一起可以按照实数的运算法则进行四则运算.

想一想

（-i）2等于什么？-1的平方根是什么？你能写出方程x²=-1的根吗？

在这种规定下，i可以与实数b相乘，再与实数a相加，结果可以写成a+bi.这样，形如a+bi（a，b∈R）的数，我们把它叫做复数，通常用字母z表示，即z=a+bi（a，b∈R）.全体复数的集合，称为复数集.一般用大写字母C表示，即C={zz=a+bi，（a，b∈R）}.如3+4i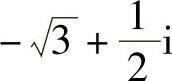，，-2i，10i等都是复数.

显然，实数集R是复数集C的真子集，即R⊆C.因此，复数可以分类如下：

这样，数集就由实数集扩充到了复数集.

复数a+bi（a，b∈R）的确定要由a与b来决定.a与b分别叫做复数的实部与虚部.复数a+bi，当b=0时，就是实数；当b≠0时，叫做虚数；当a=0，b≠0时，叫做纯虚数.

当两个复数的实部相等且虚部互为相反数时，我们称这两个复数为共轭复数.复数z的共轭复数通常用z表示，即复数z=a+bi的共轭复数是z=a-bi.如复数3+2i的共轭复数是3-2i.而实数a的共轭复数仍是它本身.

试一试

试说出下列复数的实部与虚部，并写出它们的共轭复数：

-1+2i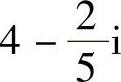，，πi，-4，0，（3x-y）+（x-1）i（x，y∈R）.

如果两个复数a+bi和c+di的实部与虚部分别相等，我们就说这两个复数相等.记作a+bi=c+di，即

a+bi=c+di⇔a=c且b=d（a，b，c，d∈R）

特别地，a+bi=0⇔a=0且b=0.

应该注意的是，两个实数可以比较大小，但是两个复数，如果不全是实数，它们之间就不能比较大小，只能说相等或不相等.如1与i，2-i与3+2i之间无大小可言.

例1　实数m为何值时，复数（m²-3m-4）+（m-6）i是

（1）实数；（2）虚数；（3）纯虚数.

分析：根据虚数与纯虚数的定义，当m-6≠0时是虚数；m²-3m-4=0且m-6≠0时是纯虚数.

解：（1）当m-6=0，即m=6时，该复数是实数；

（2）当m-6≠0，即m≠6时，该复数是虚数；

（3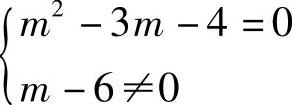），即

所以m=-1，m≠6或m=4，m≠6时，该复数是纯虚数.

例2　已知复数（5x-3y）+3xi=1+（9-y）i　（x，y∈R），求x和y的值.

分析：根据两个复数相等的定义，两个复数的实部5x-3y与1，虚部3x与9-y应分别相等，列出方程组即可求出x与y的值.

解：根据两个复数相等的定义，得方程组

解这个方程组，得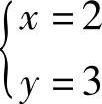

工具箱这个方程组是二元一次方程组，其解法主要有代入消元法和加减消元法.

练习

1.指出下列各数中，哪些是实数，哪些是虚数，哪些是纯虚数，哪些是复数，并分别说出它们的实部与虚部：

2.实数x取何值时，复数（x²+3x-10）+（x-2）i是实数？是虚数？是纯虚数？

3.求适合下列方程的实数x和y的值：

（1）（3x+2y）+（5x-y）i=17-2i；（2）（3x-4）+（2y+3）i=0.

2.复数的运算

两个实数可以进行四则运算，i可以与实数进行四则运算，那么两个复数z₁=2+3i和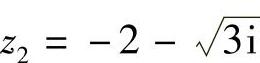

应如何进行四则运算呢？下面我们将研究一下复数的加、减、乘、除四则运算.

（1）复数的加、减法

对于复数的加、减法运算，可以把复数看成关于i的多项式，并按照多项式的加、减法法则来进行，并把最后的结果写成a+bi（a，b∈R）的形式.我们规定按照以下法则进行：设z₁=a+bi与z₂=c+di是任意两个复数，则

z₁+z₂=（a+bi）+（c+di）=（a+c）+（b+d）i

z₁-z₂=（a+bi）-（c+di）=（a-c）+（b-d）i

例3 已知z₁=2+3i，z₂=8-2i，计算z₁+z₂和z₁-z_2.

解：z₁+z₂=（2+3i）+（8-2i）=（2+8）+（3-2）i=10+i，

z₁-z₂=（2+3i）-（8-2i）=（2-8）+[3-（-2）]i=-6+5i.

综合复数的加法法则和减法法则，可以得到如下结论：两个复数的和与差仍是复数.两个复数相加、相减，只需把实部与实部、虚部与虚部分别相加、相减.

试一试

（1）计算（-3+i）+（-3-i）；

（2）计算（-3+i）-（-3-i）；

（3）举例说明两共轭复数的和为实数；

（4）举例说明两共轭复数的差为零或纯虚数.

例4　计算：（3+2i）-（7-i）+（5+6i）.

解：（3+2i）-（7-i）+（5+6i）

=（3-7+5）+[2-（-1）+6]i

=1+9i.

练习

1.计算下列各题：

（1）（3+2i）+（-1+i）；（2）（2+i）+i；

（3）5+（1+2i）；（4）（2+i）-（2-i）+（5+6i）.

2.填空题.

（1）（3+5i）+=6+2i；（2）-（1+i）=4+3i；

（3）（3+）+（-3i）=10-2i；（4）（-3i）-（4+）=2+5i.

（2）复数的乘、除法

1）复数的乘法与乘方　一般地，我们规定复数的乘法按照以下法则进行：设z₁=a+bi与z₂=c+di是任意两个复数，则

z₁·z₂=（a+bi）·（c+di）=（ac-bd）+（ad+bc）i即复数的乘法运算：把复数看成关于i的多项式，按照多项式的乘法法则来将它们相乘，把所得结果中的i²换成-1，并写成a+bi（a，b∈R）的形式.显然，两个复数的积仍是一个复数.

例5　计算：（2+i）（3-4i）.

解：原式=6-8i+3i-4i²

=10-5i.

想一想

设z₁，z₂，z3是任意三个复数，则：

（1）z₁z₂=z₂z₁成立吗？

（2）（z₁z₂）z₃=z₁（z₂z₃）是否仍然成立？

（3）z₁（z₂+z₃）=z₁z₂+z₁z₃是否仍然成立？(www.chuimin.cn)

例6　计算：（1+3i）（2-i）（1-3i）.

分析：多个复数连乘时，应该合理利用复数的乘法法则和运算技巧.

解：原式=（2-i）（1+3i）（1-3i）

=（2-i）[1-（3i）2]

=（2-i）10

=20-10i.

工具箱

a²-b²=（a+b）（a-b）

试一试

举例说明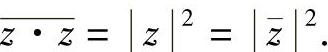

在计算复数的乘方时，实数集R中正整数指数幂的运算律在复数集C中仍然成立，即对任意的复数z₁，z₂及m，n∈N，有

z^m·zⁿ=z^m+n，（z^m）n=z^mn，（z₁·z₂）m=z^m₁·z₂^m

特别地，由i²=-1，我们可以得到

i¹=i，i²=-1，i³=-i，i⁴=1

想一想

（1）i⁵=____，i⁶=____，i⁷=____，i⁸=____.

（2）对任意的n∈N+，i⁴ⁿ=____，i⁴ⁿ⁺¹=____，i⁴ⁿ⁺²=____，i⁴ⁿ⁺³=____.

例7　已知，计算z²，z3.

分析：利用完全平方等公式进行复数的乘方运算，可以简化运算过程，提高运算速度.

解：；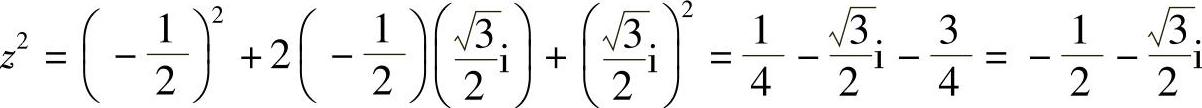

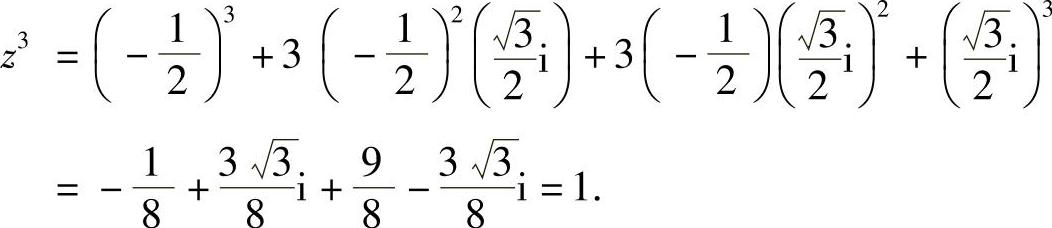
试一试

计算：（1）（1+i）2；（2）（1-i）2；（3）（1+i）4；（4）（1-i）6.

2）复数的除法　我们规定复数的除法是乘法的逆运算，把满足（c+di）（x+yi）=a+bi（c+di≠0）的复数x+yi叫做a+bi除以c+di的商（a，b，c，d，x，y∈R），记作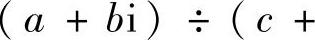

工具箱

在实数范围内，

（a±b）2=a²±2ab+b²；

（a±b）3=a³±3a²b+

3ab²±b³.

复数的除法依照下列步骤进行：

对于这一结果可以理解为：两个复数相除（除数不为零），先把它们的商写成分式，然后把分子、分母同时乘以分母的共轭复数，并把结果化简为a+bi的形式.

例8　计算：（2+i）÷（4-3i）.

解：原式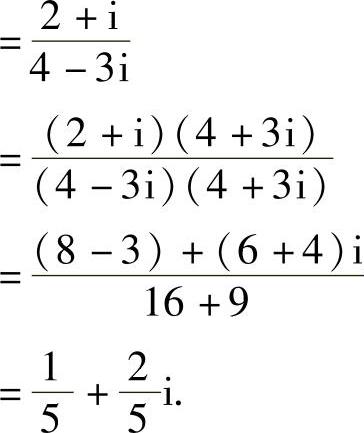

练习

1.计算下列各题：

（1）（1-2i）i；（2）（3-2i）（3+2i）；

（3）（1+i）÷（3-4i）；（4）（2+i）÷（4-3i）·（2-i）2.

2.填空题.

（1）（5-6i）2i=；（2）i⁹⁵=；

（3）（1+2i）÷（3-4i）=；

（4）

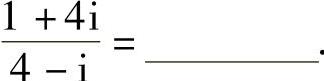
（3）实系数一元二次方程在复数范围内的解

前面我们已经知道x²+1=0有两个根i和-i，那么对于一般的实系数一元二次方程ax²+bx+c=0（a，b，c∈R，a≠0）在复数范围内的解的情况又是如何的呢？

当Δ=b²-4ac≥0时，我们知道它在实数范围内有两实数根

当Δ=b²-4ac<0时，它在实数范围内无解，下面我们在复数集C中，研究它的解的情况.

经过变形，原方程化为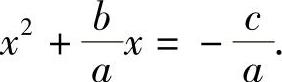

由于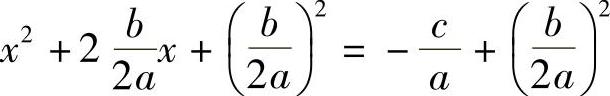

故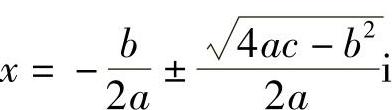

由此，实系数一元二次方程ax²+bx+c=0（a，b，c∈R，a≠0），当Δ=b²-4ac<0时，在复数集C中有两个虚根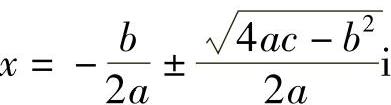.显然它们是一对共轭虚根.

想一想

如果x₁，x₂是实系数一元二次方程ax²+bx+c=0（a，b，c∈R，a≠0）当Δ=b²-4ac<0时在复数集C中的两个虚根，那么：（1）x₁+x₂等于什么？（2）x₁·x₂等于什么？（3）根与系数的关系在Δ=b²-4ac<0时还成立吗？

例9　在复数集C中，解方程x²-4x+5=0.

分析：解实系数一元二次方程时要先计算判别式Δ=b²-4ac的值，然后代入公式就可以了.

解：因为Δ=（-4）2-4×5=-4<0，

所以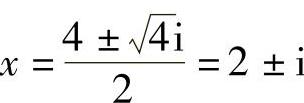，即x₁=2+i，x₂=2-i.

例10　已知实系数一元二次方程x²+px+q=0的一个根为，求它的另一个根及p和q的值.

分析：根据实系数一元二次方程有虚根时，必定是一对共轭虚根，可以求出另一根；再根据根与系数的关系列方程组求p和q的值.

解：因为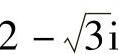是x²+px+q=0^一个根，

所以另一根为的共轭虚根，即；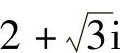

由实系数一元二次方程根与系数的关系，得

练习

1.在复数集范围内解下列方程：

（1）x²+4=0；（2）x²-2x+4=0.

2.实系数一元二次方程x²+bx+c=0的一个根为4-i，则它的另一根为，b=，c=.

3.已知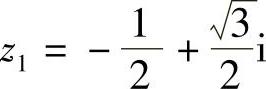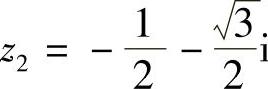，，则z³₁=，z₂³，所以z₁，z₂叫做1的立方虚根.

习题四

1.计算题.

（1）22.5i-30i+24i；（2）（3+2i）-（-1+i）；

（3）（1+i）+（3+i）；（4）（2+i）+（2-i）-（5+6i）.

2.计算下列各式的值：

（1）（2+2i）（1+i）；（2）（4-3i）（4+3i）；

（3）（2+2i）÷（3-4i）；（4）（6+i）2.

3.在复数集范围内解下列方程：

（1）x²+16=0；（2）x³+8=0.

复数的连乘以及乘法规则

相关推荐