机电应用数学-二进制数表示与转换

2023-11-22 理论教育版权反馈

【摘要】：a1a0）2，只要求出等式中的各个系数an-1，an-2，…，an-1各值，步骤如下：因此10=2练一练将十进制整数58转换为二进制整数.练习1.将下列十进制数用按权展开表示法表示.10；10；10.2.将下列二进制数用按权展开法表示.2；2.习题三1.下表是五位同学的交作业情况统计表，如果交作业用1表示，未交作业用0表示，使用二进制数表示每位同学的交作业情况.2.将2转换成十进制数.3.将10转换成二进制数.

议一议

在现实生活中，有些事物只有两种状态，例如，电路的“通”与“断”；“灯亮”与“灯灭”.那么怎样用数字记录这种现象呢？

人们想到用数字“0”与“1”来表示两种可能的结果.例如，用“1”表示“通电”，“0”表示“断电”，进而产生了一种只有两个数字的进位制——二进制.

又如，观察路口的红绿灯，如果规定“灯亮”用1表示，“灯灭”用0表示，红绿灯的各种状态见下表.

此时可以用二进制数100，010，001中的某一个来描述任意一个十字路口车辆的通行状态.

与红绿灯的例子类似，有10间教室，规定从左往右数，如果“灯亮”用1表示，“灯灭”用0表示，那么二进制数1111001010就表示了这10间教室的灯光的一种状态.

二进制的进位基数是2，在二进制中，只有0和1两个数码，二进制的进位规则是由低位向高位“逢二进一”，即每位计满2就向高位进1.例如，（1101）2就是一个二进制数.不同数位的数码表示的值不同，各位的权值是以2为底的连续整数幂，从右向左递增.

对于任意一个二进制数N，用位置计数法表示为

（N₂）=（a_n-1a_n-2…a₁a₀a_-1a_-2…a_-m）2

用按权展开法表示为

其中，a_i为0或1；n为整数部分的位数；m为小数部分的位数.

通常，对二进制数的表示，可以在数字的右下角标注2或B.

例1　将下列二进制数用按权展开法表示：

（1）（11001）2；（2）（0.110101）2；（3）（101.101）2.

解：（1）（11001）2=1×2⁴+1×2³+0×2²+0×2¹+1×2⁰；

（2）（0.110101）2=1×2^-1+1×2^-2+0×2^-3+1×2^-4+0×2^-5+1×2^-6；

（3）（101.101）2=1×2²+0×2¹+1×2⁰+1×2^-1+0×2^-2+1×2^-3.

练一练

将下列二进制数用按权展开法表示：

（1）（1100.01）2；（2）（101.11）2.

例2 将二进制数（11010.101）2转换成十进制数.

解：（11010.101）2=1×2⁴+1×2³+0×2²+1×2¹+0×2⁰+1×2^-1+0×2^-2+1×2^-3

=16+8+2+0.5+0.125

=（26.625）10.

例3 将十进制整数157转换为二进制数.(www.chuimin.cn)

解：设（157）10=（a_n-1a_n-2…a₁a₀）2，只要求出等式中的各个系数a_n-1，a_n-2，…，a₁，a₀便得到二进制整数.

由于

（157）10=（a_n-1a_n-2…a₁a₀）₂

=a_n-1×2^n-1+a_n-2×2^n-2+…+a₁2¹+a₀2⁰

=2（a_n-1×2^n-2+a_n-2×2^n-3+…+a₁）+a0

等式两端除以2，得

此式表明a₀为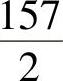的余数，故a₀=1.上式又可写成

即

78=2（a_n-1×2^n-3+a_n-2×2^n-4+…+a₂）+a1

两端再除以2，即得a₁为的余数，故a₁=0.

用同样的方法继续下去，可以得到a₂，a₃，…，a_n-1各值，步骤如下：

因此

（157）10=（10011101）2

练一练将十进制整数58转换为二进制整数.

练习

1.将下列十进制数用按权展开表示法表示.

（1）（125.056）10；（2）（10501）10；（3）（0.3463）10.

2.将下列二进制数用按权展开法表示.

（1）（1101.01）2；（2）（111.11）2.

习题三

1.下表是五位同学的交作业情况统计表，如果交作业用1表示，未交作业用0表示，使用二进制数表示每位同学的交作业情况.

2.将（101100.1011）2转换成十进制数.

3.将（12.3）10转换成二进制数.（精确到小数点后3位）

机电应用数学-二进制数表示与转换

相关推荐