首页理论教育机电应用数学：数的认识与区别

机电应用数学：数的认识与区别

2025-09-30 理论教育版权反馈

【摘要】：回顾与思考初中学过的数，它们的关系可以归纳如下：议一议有理数和无理数有什么区别？数的集合简称数集，全体非负整数的集合，通常简称非负整数集，记作N，非负整数集内排除0的集合，也称正整数，记作N+；全体有理数的集合，简称有理数集，用Q表示；全体实数的集合，简称实数集，用R表示.为了方便，还用Q+表示正有理数集，Q-表示负有理数集；R+表示正实数集，R-表示负实数集.我们通常用大写拉丁字母A，B，C，…

回顾与思考

初中学过的数，它们的关系可以归纳如下：

议一议　有理数和无理数有什么区别？

数的集合简称数集，全体非负整数的集合，通常简称非负整数集（或自然数集），记作N，非负整数集内排除0的集合，也称正整数，记作N+；全体有理数的集合，简称有理数集，用Q表示；全体实数的集合，简称实数集，用R表示.为了方便，还用Q+表示正有理数集，Q-表示负有理数集；R+表示正实数集，R-表示负实数集.

我们通常用大写拉丁字母A，B，C，…表示集合，用小写拉丁字母a，b，c，…表示集合中的元素.

如果a是集合A的元素就说a属于集合A，记作a∈A，如果a不是集合A中的元素，就说a不属于集合A，记作a∉A.

例1　用符号“∈”或“∉”填空.

解：（1）∈；（2）∉；（3）∈；（4）∉；（5）∈；（6）∈；（7）∉；（8）∈.

例2　在数轴上表示下列各数，并求出它们的相反数和绝对值.

解：以上各数在数轴上的表示如图1-1所示.

图1-1(https://www.chuimin.cn)

相反数分别为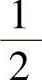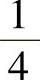，，0，-3，-4.5；

绝对值分别为，，0，3，4.5.

练习

1.用符号“∈”或“∉”填空.

2.下表记录了某日我国几个城市的平均气温：

（1）将各城市的平均气温从高到低进行排列；

（2）在地图上找到这几个城市的位置，并将它们从北到南进行排列.

习题一

1.用符号“∈”或“∉”填空.

2.判断下列各题所表示的关系是否正确.