首页理论教育矩阵运算规则-虚拟现实辅助结构可装配性设计

矩阵运算规则-虚拟现实辅助结构可装配性设计

2023-11-22 理论教育版权反馈

【摘要】：即我们称式中的aij为矩阵A的元素，a的第一个注脚字母i(i=1，2，…当矩阵A的元素仅有一行或一列时，则称它为行矩阵或列矩阵。如果在对角矩阵中所有的主对角线元素都相等且均为1，如，则称为单位矩阵。矩阵的乘法是可结合的。上述方程组就是测量平差中的误差方程组，故知式即为误差方程组的矩阵表达式。式中称为改正数阵，称为误差方程组的系数阵，称为未知数阵，称为误差方程组的常数项阵。

1.矩阵的定义

一般而言，所谓矩阵就是由一组数的全体，在括号“[]”内排列成m行n列(横的称行，纵的称列)的一个数表，并称它为m×n矩阵。

矩阵通常是用大写字母A、B、…来表示。例如一个m行n列的矩阵可以简记为A=(aij)，或。即

我们称式(10-6)中的aij为矩阵A的元素，a的第一个注脚字母i(i=1，2，…，m)表示矩阵的行数，第二个注脚字母j(j=1，2，…，n)表示矩阵的列数。

当m=n时，则称A=(aij)为n阶方阵，并用(aij)nm表示。当矩阵A的元素(aij)仅有一行或一列时，则称它为行矩阵或列矩阵。设两个矩阵，有相同的行数和相同的列数，而且它们的对应元素一一相等，即aij=bij，则称该两矩阵相等，记为A=B。

2.三角形矩阵

以i=j的元素组成的对角线为主对角线，构成这个主对角线的元素称为主对角线元素。如果在方阵中主对角线一侧的元素全为零，而另外一侧的元素不为零或不全为零，则该矩阵叫作三角形矩阵。例如，以下矩阵都是三角形矩阵。

3.单位矩阵与零矩阵

在方阵中，如果只有i=j的元素不等于零，而其他元素全为零，如

则称为对角矩阵，可记为A=diag(a11，a22，…，amn)。如果在对角矩阵中所有的主对

角线元素都相等且均为1，如 pagenumber_ebook=240,pagenumber_book=227 ，则称为单位矩阵。单位矩阵常用E来表示，即

当矩阵中所有的元素都等于零时，叫作零矩阵，并用符号“O”来表示。

4.矩阵的加法

矩阵A=(aij)m×n和矩阵B=(bij)m×n相加时，必须要有相同的行数和列数。如以C=(cij)m×n表示矩阵A及矩阵B的和，则有

式中，cij=aij+bij。即矩阵C的元素等于矩阵A和矩阵B的对应元素之和。由上述定义可知，矩阵的加法具有下列性质(设A、B、C都是m×n矩阵)。

(1)交换律:A+B=B+A。

(2)结合律:(A+B)+C=A+(B+C)。

5.数与矩阵的乘法

我们定义用k右乘矩阵A或左乘矩阵A，其积均等于矩阵A=(aij)m×n中的所有元素都乘上k之后所得的矩阵。如

由上述定义可知，数与矩阵相乘具有下列性质(设都是m×n矩阵，k、h为任意常数):

6.矩阵的乘法

若矩阵乘矩阵，则只有在前者的列数等于后者的行数时才有意义。矩阵的元素Cij的计算方法定义为第一个矩阵第i行的元素与第二个矩阵第j列元素对应乘积的和。若

则矩阵的元素由定义知其计算公式为(www.chuimin.cn)

【例10-1】设有两矩阵为: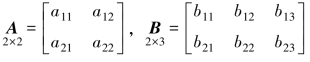 pagenumber_ebook=241,pagenumber_book=228 ，试求该两矩阵的积。

【解】由于A矩阵的列数等于B矩阵的行数，故可乘，其结果设为C:

其中

【例10-2】已知: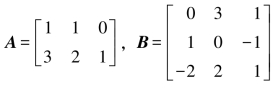 pagenumber_ebook=242,pagenumber_book=229 ，试求该两矩阵的积。

【解】计算结果如下:

矩阵的乘法具有下列性质。

(1)通常矩阵的乘积是不可交换的。

(2)矩阵的乘法是可结合的。

(3)设A是m×n矩阵，B、C是两个n×t矩阵，则有:A(B+C)=AB+AC。

(4)设A是m×n矩阵，B是n×t矩阵。则对任意常数k有:k(AB)=(k A)B=A(k B)。

【例10-3】用矩阵表示的某一组方程为

式中

试将矩阵公式展开，列出方程组。

【解】现将式(10-9)代入式(10-8)得

将式(10-10)右边计算整理得

可得方程组:

可见，上述方程组可以写成式(10-8)的矩阵形式。上述方程组就是测量平差中的误差方程组，故知式(10-8)即为误差方程组的矩阵表达式。式中称为改正数阵，　称为误差方程组的系数阵，称为未知数阵，　称为误差方程组的常数项阵。

【例10-4】设由n个观测值列出r个条件式如下，试用矩阵表示。

【解】现记

则条件方程组可用矩阵表示成

式中，称为条件方程组的系数阵，　称为改正数阵，称为条件方程组的闭合差阵列。