,如果K0远小于K-1,则米氏常数Km的含义:Km是酶促反应速度达到最大反应速度一半时的底物浓度。其数值为一个常数,但可在严格规定条件下测定,通常以mo l/L表示。实质上Km是酶与底物亲和力的量度,Km值大表明K1小,E和S的亲和力小。例如,酵母菌脱羧酶的反应,经过实验求得表5-2所列的数据。并求出该酶的Km及vm。......
2023-11-22
1902年Henrri在研究蔗糖酶催化水解蔗糖的反应中发现其反应速度随着底物的浓度增加而增加,当其底物增加到一定浓度时,酶催化反应速度达到恒定状态即最大值,底物浓度[S]对速度v作图,便形成“双曲线”图形,并提出中间产物学说以解释酶的催化作用原理。
1913年L.Michaelis和M.L.Menten根据中间产物学说对“双曲线”反应图形加以数学推导,提出所谓快速平衡假定(rapid equilibrium,即R.E.假定):
(1)测定的速度为反应的初速度,底物浓度[S]消耗很少,仅占[S]原始浓度的5%以内,故在测定反应速度所需时间内,P的生成极少,(P+E)的逆转可以忽略不计。
(2)底物浓度[S]大大地超过酶的浓度[E]。因此,ES的形成不会明显地降低底物浓度[S]。例如,[S]=10-3mol/L,而[E]=10-9~10-8mol/L,所以即使所有[E]都变为ES,此时[S]的降低仍可忽略不计。
(3)ES解离成E +S的速度也大大超过ES分解而形成(P+E)的速度,即K-1≫K0或者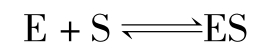 的可逆反应在测定初速度v的时间内已达到动态平衡,而少量P的生成不影响这个平衡,故称为快速平衡假定。
的可逆反应在测定初速度v的时间内已达到动态平衡,而少量P的生成不影响这个平衡,故称为快速平衡假定。
假设E S形成E +S的解离常数为Ks,因此:
若E的原始浓度为[E0],在反应平衡时,E的浓度变为([E0]-[ES]),而此时根据上述假定(2),S的浓度[S]保持不变。故式(5-1)变为:
由于反应速度v取决于[ES],即v=K0[ES],
当[S]为极大时,全部E转变为ES,[ES] = [E0],此时v=vm(最大反应速度),故vm=K0[E0],即:
将式(5-5)和式(5-6)代入式(5-4),可得:
式(5-8)即为M-M两氏根据快速平衡假定推导出的米氏方程式。
如果将式(5-8)移项整理可得:
由于vm和Ks均为常数,而v及[S]为变量,故式(5-11)实际上可写成(x-a)(y+b)=k,实质上为典型的双曲线方程,可见米氏方程式与试验结果是相符的。
设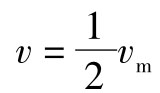 ,代入式(5-8),则可得:
,代入式(5-8),则可得:
由式(5-14)说明,ES的解离常数Ks,即当反应的初速度v为最大反应速度vm的1/2时所需的底物浓度,故Ks的单位可以用物质的量(mol/L)浓度单位表示。
Ks的倒数1/Ks=K1/K-1为亲和常数,可代表E和S形成中间复合物E S的亲和力,Ks很小或1/Ks很大,说明ES不易解离成(E+S),而E和S都很容易形成ES,只要很少的[S]便可使v达到最大反应速度的1/2。
所谓[S]的极小或极大值,实际上可看作Ks和[S]的相对比值。如Ks和[S]相比要大得多,则式(5-8)分母中的[S]可忽略不计,则:
此式说明反应对底物为一级反应,其速度与[S]成正比,反之,当Ks和[S]相比小得多,则式(5-8)分母的Ks可忽略而成为:
此式,反应速度达到最大的恒定值,反应速度与底物浓度无关,该化学反应属零级反应。
1925年Brigg-Haldane认为,快速平衡假定中K0不能远小于K-1。因此,他们提出了一个恒态(Steady-State)学说并对米氏常数的推导加以修正。该学说在公式推导时,保留了米氏的前两点假定,而将第三点假定修改为恒态假定,其恒态假定如图5-2所示。
图5-2 恒态假定示意图
根据B-H两氏的恒态学说,其反应式为:
生成ES的速度为
ES消失的速度为
当该反应处于恒态时,ES生成和消失的速度相等。
因为
则
Brigg和Haldane将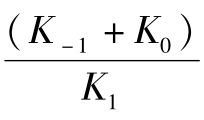 的复合常数以Km为代表,Km即为米氏常数(Michaelis constant),因此:(www.chuimin.cn)
的复合常数以Km为代表,Km即为米氏常数(Michaelis constant),因此:(www.chuimin.cn)
同样可用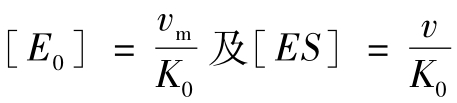 ,代入式(5-24),则:
,代入式(5-24),则:
此式与式(5-8)一样,区别在于用Km取代Ks,为了纪念Michaelis和Menten两人,两式均称为米氏方程式,均为双曲线动力学图形。但Km不同于Ks,因为Km还取决于K0的大小。
如果当K0>K-1时,Km也大于Ks,其差值为K0/K1,此时1/Km就大于E和S的亲和常数。
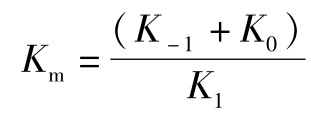 ,如果K0远小于K-1,
,如果K0远小于K-1,
则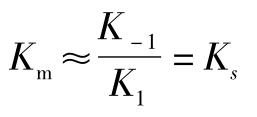
米氏常数Km的含义:Km是酶促反应速度达到最大反应速度一半时的底物浓度。其数值为一个常数,但可在严格规定条件下测定,通常以mo l/L表示。实质上Km是酶与底物亲和力的量度,Km值大表明K1小,E和S的亲和力小。反之,Km值小表明K1大,E和S的亲和力大。一些酶的Km如表5-1所示。
表5-1 一些酶的Km值
K m及vm可以根据两组不同底物浓度的试验数据代入公式,然后解二元一次联立方程式计算。但此法不够简便,而且因v不易准确测定,故Km不易准确计算。
1934年Lineweaver和Burk提出双倒数法作图求取Km。将米氏方程式两边变为倒数,即为:
这个公式相当于y=ax+b,是一个直线方程式,其斜率为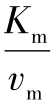 ,截距为
,截距为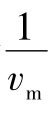 ,直线与
,直线与 轴的交点等于
轴的交点等于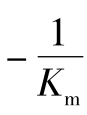 。因为
。因为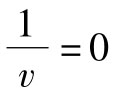 时,
时,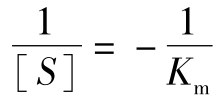 ,如图5-3(1)所示。
,如图5-3(1)所示。
例如,酵母菌脱羧酶的反应,经过实验求得表5-2所列的数据。根据这个实验就可用方格纸以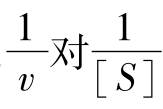 作图,如图5-3(2)所示。并求出该酶的Km及vm。
作图,如图5-3(2)所示。并求出该酶的Km及vm。
图5-3 作图法
表5-2 酵母菌脱羧酶反应速度
由于
故
1959年Eadie-Hofstee提出第二种作图法,将米氏方程移项整理后可得:
故
此式为一个直线方程式,作图结果如图5-4所示。
当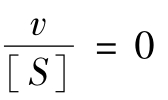 时,截距为vm。
时,截距为vm。
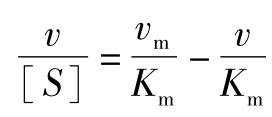 ,当
,当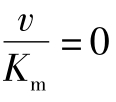 时,截距为
时,截距为 。
。
1974年Eisenthal和Cornish-Bowden提出第三种作图法。
在一定酶浓度时,米氏方程双倒数关系可以整理为式(5-31)
即:
当vm对Km作图,可以得到一条直线,如图5-5所示。当Km=0,v=Vm,当vm=0,Km=-[S]
图5-4 Eadie-Hofstee作图法
图5-5 Eisenthal和Cornish-Bowden作图法
上述三种作图法求取Km在研究和实际工作中均有所应用。由于第一种作图法比较简便,较为普遍采用,其缺点是若[S]浓度低时,与v所成的点所占的分量较重,易造成一些不够精确的vm值和Km值,而后两种作图法不存在此问题。
有关食品酶学导论的文章

,如果K0远小于K-1,则米氏常数Km的含义:Km是酶促反应速度达到最大反应速度一半时的底物浓度。其数值为一个常数,但可在严格规定条件下测定,通常以mo l/L表示。实质上Km是酶与底物亲和力的量度,Km值大表明K1小,E和S的亲和力小。例如,酵母菌脱羧酶的反应,经过实验求得表5-2所列的数据。并求出该酶的Km及vm。......
2023-11-22

酶促反应速度和普通化学反应一样,可用单位时间内底物减少量或产物增加量来表示。反应速度即图中曲线的斜率。酶反应速度,是对初速度而言。在一定条件下,酶所催化的反应速度称为酶活力。由于反应底物或产物可显示不同吸收光谱,光吸收与浓度成正比,光吸收改变的速率与酶活力也成正比,因而可用分光光度计来进行测定酶反应的情况。......
2023-11-22

酶是在活细胞中合成并在胞内或胞外介质中存在的。胞内酶在细胞内存在部位和结合状态比较复杂,因而抽提难度较大。酶的抽提目的是将尽可能多的酶或尽可能少的杂质从原料组织和细胞中引入溶液,以利于酶的纯化。但此法用于酶的大量提取有一定局限性。经丙酮处理的细胞干粉称为丙酮粉。丙酮还能除去细胞膜部分脂肪,更有利于酶的提取。根据酶在细胞内结合状态以及其溶解程度,酶的抽提可分为水溶法和有机溶剂法两种。......
2023-11-22

因而,各种各样的发酵酿造食品均与酶的应用紧密相关。在生产中采用黑曲糖化酶、真菌β-淀粉酶和脱支酶等。目前此法仍在试验阶段,采用的设备为固定床和流化床生物反应器。在酒精生产中,淀粉质原料的蒸煮是一个关键工序。在酿造生产中此酶适用于蒸煮前的调浆工序,其最适温度为90~105℃,pH为5.5~7.0。酶法应用于白酒、黄酒、食醋和酱油的生产中,主要在加曲糖化过程中采用外加糖化酶,可加速糖化工序,便于缩短生产周期。......
2023-11-22

对酶促作用的影响同抑制作用相反,许多酶促反应必须有其他适当物质存在时才能表现酶的催化活性或加强其催化效力,这种作用称为酶的激活作用,引起激活作用的物质称为激活剂。至于无机阴离子对酶的激活作用,在实践中也是常见的现象。若酶原被具有活力的同种酶所激活,则称为酶的自身激活作用。而酶的活性部位往往只能作用于底物的一种解离状态。当温度超过酶的最适温度时,酶蛋白就会逐渐产生变性作用而减弱甚至丧失其催化活性。......
2023-11-22

20世纪70年代初实现了DNA重组技术,极大地推动着食品科学与工程的发展,也促使酶学研究进入新的发展阶段。现代食品酶学发展有如下几个新的突破:1.酶及细胞固定化技术的开发应用作为一种催化剂,在催化过程中自身不发生变化,可以反复使用。酶及产酶细胞的固定化技术从酶学理论到生产实践得到迅速的发展,引起食品、发酵工业一场大变革。......
2023-11-22

几乎所有的动植物酶都可以从微生物细胞中获得,而且微生物容易变异,可以通过菌种改良,进一步提高酶的产量。因此,工业酶制剂几乎都用微生物发酵法进行大规模制造的。产酶的微生物主要是细菌、真菌、霉菌和放线霉等。......
2023-11-22

酶的分离、纯化属生物工程的下游过程。酶的产量是以活力单位表示的,在整个分离过程中每一步都需要进行比活力和总活力的检测、比较。只有这样才能确定酶的分离、纯化程度。要了解酶的实际纯度,尚需采用电泳等测定方法。一般试剂级及药用级用酶纯度要求高,则采取提纯倍数高的方法。而食品级酶在整个分离、纯化工程中要注意卫生,防止污染,各方面均需综合考虑。......
2023-11-22
相关推荐