设a是非零常数,f是已知函数,则称yt+1+ayt=f(t=0,1,2,…).上式就是式()对应的一阶常系数齐次线性差分方程.()如果函数yt=φ代入式()或(式()),使之对t=0,1,2,…......
2023-10-27
一、差分与差分方程的一般概念
定义6.3 设函数y=f(x),记为yx,则差yx+1-yx称为yx的一阶差分,简称为差分,记为Δyx,即
Δyx=yx+1-yx.
定义6.4 yx的一阶差分的差分
Δ(Δyx)=Δ(yx+1-yx)=(yx+2-yx+1)-(yx+1-yx),记为Δ2yx,称为yx的二阶差分,即
Δ2yx=Δ(Δyx)=yx+2-2yx+1+yx.
同样定义三阶差分,四阶差分,…
Δ3yx=Δ(Δ2yx),Δ4yx=Δ(Δ3yx),…
二阶及二阶以上的差分统称为高阶差分.
由差分的定义,可知差分具有如下性质:
1)ΔC=0(C为常数);
2)ΔCyx=CΔyx(C为常数);
3)Δ(yx+zx)=Δyx+Δzx.
例1 求Δ(x2),Δ2(x2),Δ3(x2).
解 设yx=x2,那么
Δyx=Δ(x2)=(x+1)2-x2=2x+1,
Δ2yx=Δ2(x2)=Δ(2x+1)=[2(x+1)+1]-(2x+1)=2,
Δ3yx=Δ(Δ2yx)=Δ(2)=2-2=0.
例2 设yx=λx,求Δyx.
解 yx+1=λx+1=λ·λx=λyx,于是
Δyx=yx+1-yx=(λ-1)λx.
定义6.5 含有自变量、未知函数以及未知函数差分的方程,称为差分方程.方程中含有未知函数差分的最高阶数称为差分方程的阶.
n阶差分方程的一般形式为
F(x,yx,Δyx,Δ2yx,…,Δnyx)=0 (6-25)
将Δyx=yx+1-yx,
Δ2yx=yx+2-2yx+1+yx,
Δ3yx=yx+3-3yx+2+3yx+1-yx,
︙代入式(6-25),则方程变成
F(x,yx,yx+1,…,yx+n)=0 (6-26)
反之,方程式(6-26)也可以化为式(6-25)的形式.因此差分方程也可以定义如下:
定义6.6 含有自变量以及未知函数两个以上(含两个)时期值的符号的方程,称为差分方程.方程中含有未知函数下标的最大值与最小值的差称为差分方程的阶.
比如,二阶差分方程yx+2-2yx+1-yx=3x,可以化为
yx-2yx-1-yx-2=3x-2.
事实上,将原方程左边写成
(yx+2-yx+1)-(yx+1-yx)-2yx=Δyx+1-Δyx-2yx=Δ2yx-2yx.
则原方程可以化为Δ2yx-2yx=3x.
定义6.7 如果一个函数代入差分方程后,方程两边恒等,则称此函数为该差分方程的解.
比如,差分方程yx+1-yx=2,把函数yx=15+2x代入此方程,则左边=[15+2(x+1)]-(15+2x)=2=右边,故yx=15+2x是方程的解.
在实际问题中,往往要根据系统在初始时刻所处的状态,对差分方程附加一定的条件,这种附加条件称之为初始条件.满足初始条件的解称为特解.如果差分方程的解中含有任意常数的,且任意常数的个数恰好等于方程的阶数,则称它为差分方程的通解.
比如,对于一阶差分方程Δyx=0,易知它的通解是yx=A(A是任何实常数).
二、一阶常系数线性差分方程
形如yx+1+ayx=f(x)(a≠0,且a为常数) (6-27)的方程称为一阶常系数线性差分方程.
其中,f(x)为已知函数,yx是未知函数.解差分方程就是求出方程中的未知函数.式(6-27)中当f(x)≠0时,称之为非齐次的,否则称之为齐次的.即
yx+1+ayx=0 (6-28)该式称为与式(6-27)对应的齐次差分方程.
下面介绍一阶常系数差分方程的解法
1.齐次方程的解
显然,yx=0是方程式(6-28)的解.
若yx≠0,则有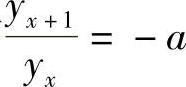 ,即{yx}是以A为首项,公比为-a的等比数列,于是方程式(6-28)的通解为yx=Aax.当a=1时,通解为yx=A.
,即{yx}是以A为首项,公比为-a的等比数列,于是方程式(6-28)的通解为yx=Aax.当a=1时,通解为yx=A.
2.非齐次方程的解法
由前面的概念可以看出,差分方程与微分方程有许多相似之处.微分方程描述变量连续变化过程,而差分方程一般描述变量离散变化过程.当自变量间隔很小时,差分可以看成微分的近似.因此,差分方程和微分方程在解的结构、解的性质以及求解方法上基本相似.比如,若yx∗是式(6-27)的一个特解,Yx是式(6-28)的解,则yx=yx∗+Yx是式(6-27)的解.事实上,

两式相加得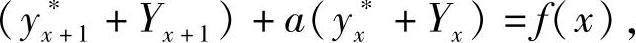 即yx=yx∗+Yx是式(6-27)的解.
即yx=yx∗+Yx是式(6-27)的解.
因此,如果yx∗是式(6-27)的一个特解,则
yx=yx∗+Aax
就是式(6-27)的通解.这样,为求式(6-27)的通解,只需求出它的一个特解即可.
下面来讨论当f(x)是某些特殊形式的函数时式(6-27)的特解.
情形1 f(x)=pn(x)(n次多项式),则方程式(6-27)为
yx+1+ayx=pn(x),(6-29)
如果yx是m次多项式,则yx+1也是m次多项式,并且当a≠-1时,yx+1+ayx仍是m次多项式,因此若yx是式(6-29)的解,应有m=n.
于是,当a≠-1时,设yx∗=B0+B1x+…+Bnxn是式(6-29)的特解,将其代入式(6-29),比较两端同次项的系数,确定出B0,B1,…,Bn,便得到式(6-29)的特解.
当a=-1时,方程式(6-29)成为yx+1-yx=pn(x),或Δyx=pn(x).因此,yx应是n+1次多项式,此时设特解为yx∗=x(B0+B1x+…+Bnxn),代入式(6-27),比较两端同次项系数来确定B0,B1,…,Bn,从而可得特解.
特别地,pn(x)=C(C为常数),则式(6-29)为
yx+1+ayx=C (6-30)
当a≠-1时,设yx∗=k,代入式(6-30)得 ,所以特解为
,所以特解为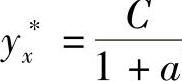 .
.
当a=-1时,设yx∗=kx,代入式(6-30),得k=C,得特解为yx∗=Cx.
例3 求差分方程yx+1-3yx=-2的通解.
解 a=-3≠1,C=-2,对应齐次方程的通解为Y=A3x.非齐次方程的特解为
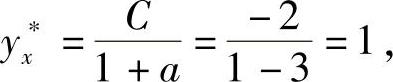
所以,差分方程的通解为yx=1+A3x.
例4 求差分方程yx+1-2yx=3x2的通解.
解 由a=-2知,对应齐次方程的通解为Y=A2x.
设yx=B0+B1x+B2x2是方程的解,将它代入方程,则有
B0+B1(x+1)+B2(x+1)2-2B0-2B1x-2B2x2=3x2,整理得(-B0+B1+B2)+(-B1+2B2)x-B2x2=3x2,比较同次项系数得

解得B0=-9,B1=-6,B2=-3,方程的特解为yx=-9-6x-3x2,而相应的齐次方程的通解为A2x,于是得差分方程的通解yx=-9-6x-3x2+A2x.
例5 求差分方程yx+1-yx=3x2+x+4的通解.
解 由a=-1知,对应齐次方程的通解为Y=A.
设特解为yx∗=x(B0+B1x+B2x2),代入原方程得
3B2x2+(2B1+3B2)x+(B0+B1+B2)=3x2+x+4,(www.chuimin.cn)
比较系数得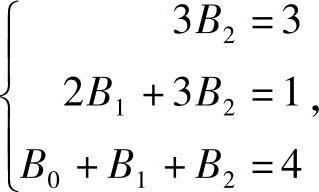
解得B0=4,B1=-1,B2=1,
特解为yx∗=x(4-x+x2).
因而得通解yx=x3-x2+4x+A.
情形2 f(x)=cbx(其中c、b均为常数,且b≠1),即
yx+1+ayx=cbx.(6-31)
当b≠-a时,设yx∗=kbx为特解,代入式(6-31)并化简,得k(b+a)=c,所以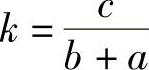 ,于是
,于是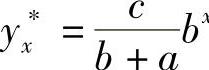 .
.
当b=-a时,设yx∗=kxbx为特解,代入式(6-31)并化简,得 ,所以特解为
,所以特解为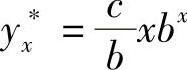 .
.
例6 求差分方程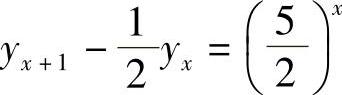 的通解.
的通解.
解 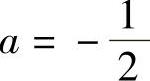 ,
, ,c=1,对应齐次差分方程的通解为
,c=1,对应齐次差分方程的通解为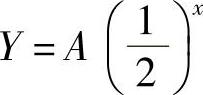 ,非齐次差分方程的特解为
,非齐次差分方程的特解为 ,所以,原差分方程的通解为
,所以,原差分方程的通解为

例7 求差分方程yx+1-2yx=3·2x满足初始条件y0=4的特解.
解 由a=-2知,对应齐次差分方程的通解为Y=A·2x.由于b=2=-a,则特解为 ,所以原方程的通解为
,所以原方程的通解为 .
.
代入初始条件y0=4,解得A=4,所以原方程的特解为
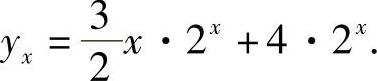
三、二阶常系数线性差分方程
形如
yx+2+ayx+1+byx=f(x) (6-32)的方程称为二阶常系数线性非齐次差分方程.
当f(x)≡0时,式(6-32)变为
yx+2+ayx+1+byx=0 (6-33)称为二阶常系数线性齐次差分方程.
1.二阶常系数线性差分方程解的结构
定理6.5 设y1x与y2x都是式(6-33)的解,则y1x与y2x的线性组合
yx=A1y1x+A2y2x也是式(6-33)的解.
定理6.6 设y1x与y2x都是式(6-33)的解,且y1x与y2x线性无关,则
yx=A1y1x+A2y2x便是式(6-33)的通解,其中A1,A2是任意常数.
定理6.7 设yx=A1y1x+A2y2x是式(6-33)的通解,且yx∗是式(6-32)的一个特解,则
Y=yx∗+A1y1x+A2y2x是式(6-32)的通解.
由上面的定理,为了求出方程式(6-32)的通解,只需先求出相应的齐次方程(6-33)的两个线性无关的通解,再求出式(6-32)的一个特解即可.
2.二阶常系数线性齐次差分方程的解
与相应的二阶微分方程类似,可设方程式(6-33)具有形如yx=λx的特解,代入式(6-33)并消去λx,得
λ2+aλ+b=0 (6-34)
式(6-34)称为式(6-33)的特征方程.根据方程式(6-34)的根的不同情况,讨论如下.
1)设特征方程式(6-34)有两个不同的实根λ1≠λ2,则式(6-33)有两个线性无关的特解y1x=λx1,y2x=λx2.
因此式(6-33)的通解便是yx=A1λx1+A2λx2.
2)设特征方程式(6-34)有两个相同的实根λ1=λ2=λ,则y1x=λx是式(6-33)的一个特解.仿微分方程可求出另一特解
y2x=xλx.于是式(6-33)的通解是
yx=(A1x+A2)λx(A1,A2是任意常数).
3)设式(6-33)的特征方程式(6-34)有两个共轭的复数根
λ1=α+βi,λ2=α-βi.
可以证明方程方程式(6-33)有两个线性无关的实数特解
y1∗=rxcosβx,y2∗=rxsinβx.其中,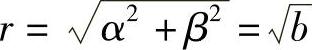 ,
, ,
, ,
,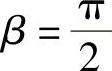 因此式(6-33)的通解是yx=rx(A1cosβx+A2sinβx).
因此式(6-33)的通解是yx=rx(A1cosβx+A2sinβx).
例8 假设有人年初买了一对小兔子,经一个月生长,长成了大兔子,便开始繁殖,且每月都生一对小兔子,而小兔子又遵循年初那对兔子的繁殖规律,问第x个月兔子有多少对(假设兔子都不死亡)?
解 设第x个月兔子的对数是yx,则第x+2个月的兔子数目可以这样得到:
第x+1个月的兔子在第x+2个月依然存在,但它们有大有小不一定都生小兔子,而第x个月的所有兔子到第x+2个月都生一对兔子,因此有yx+2=yx+1+yx,即yx+2-yx+1-yx=0,且y0=y1=1.
特征方程是λ2-λ-1=0.
求得两个根 .于是原问题的解是
.于是原问题的解是 ,确定A1,A2之后,便得
,确定A1,A2之后,便得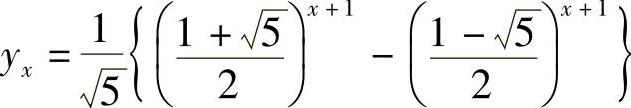 .
.
3.二阶常系数线性非齐次方程的解法
与一阶非齐次差分方程类似,二阶非齐次差分方程的特解同样可以采用待定系数法求.非齐次方程特解类型与方程右端项f(x)有关,具体参见表6-1。
表6-1

(续)

例9 求差分方程yx+2+yx+1-2yx=12的通解及y0=y1=0时的特解.
解 相应齐次方程yx+2+yx+1-2yx=0的特征方程为
λ2+λ-2=0,解得特征根为λ1=-2,λ2=1,于是齐次方程的通解是
yx=A1(-2)x+A2.
由于a+b+1=0,且a=1≠-2,故设原方程的一个特解是
yx∗=a0x,代入原方程,得a0=4,因此,特解是
yx∗=4x.
于是,原方程的通解为Y=A1(-2)x+A2+4x.
由y0=0,y1=0得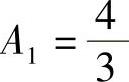 ,
,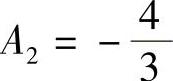 .故所求特解为
.故所求特解为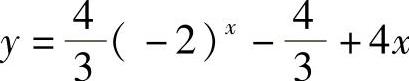 .
.
例10 求差分方程yx+2+5yx+1+4yx=x的通解.
解 对应齐次方程的特征方程是λ2+5λ+4=0,
特征根为λ1=-1,λ2=-4,
齐次方程的通解yx=A1(-1)x+A2(-4)x.
由于a+b+1=10≠0,故设yx∗=ax+b为非齐次方程的一个特解,代入原方
程得

解得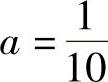 ,
,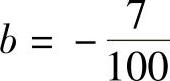 ,于是
,于是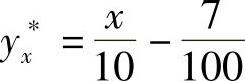 .
.
原方程的通解为

例11 求差分方程yx+2-10yx+1+25yx=3x的通解.
解 对应齐次方程的特征方程是
λ2-10λ+25=0,
解得特征根为λ1=λ2=5,
于是齐次方程通解是yx=(c1+c2x)·5x.
又因为d=3不是特征根,故可设非齐次特解是yx∗=A·3x,代入原方程求得 .
.
故原方程的通解为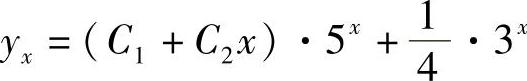 .
.
有关高等数学(上、下册)的文章

设a是非零常数,f是已知函数,则称yt+1+ayt=f(t=0,1,2,…).上式就是式()对应的一阶常系数齐次线性差分方程.()如果函数yt=φ代入式()或(式()),使之对t=0,1,2,…......
2023-10-27

一、罗尔定理定理3.1 若函数f(x)满足条件:1)在[a,b]上连续;2)在(a,b)内可导;3)在区间端点处的函数值相等,即f(a)=f(b);则在(a,b)内至少存在一点ξ,使得f′(ξ)=0.证 如图3-1所示,因为f(x)在[a,b]上连续,由连续函数的性质,f(x)在[a,b]上必有最大值M和最小值m.1)如果m=M,则f(x)在[a,b]上恒为常数M,因此在(a,b)内恒有f(x)=......
2023-11-22

高斯差分算子是在多尺度空间中寻找稳定有效的特征区域。图4-1 高斯拉普拉斯函数与高斯差分函数图4-2 高斯金字塔和高斯差分金字塔的构造示意图限于篇幅,图4-2只给出了第一层和第二层高斯差分图像的计算。如图4-2中右图的五角星符号所标识,由于需要与相邻尺度的点进行比较,所以在每层高斯差分金字塔的一组图像中只能检测到两个尺度的极值点。......
2023-06-28

离散系统的动态过程用建立在差分、差商等概念基础上的差分方程来描述。k阶线形差分方程的一般形式为式中,r——输入量;c——输出量。各阶差分的变换函数例8-7 用Z变换法求二阶差分方程:y(k+2)+3y(k+1)+2y=r。解:利用超前定理,对差分方程进行Z变换,得z2Y-z2y-zy+3[zY-zy]+2Y=R将已知条件代入上式,得所以,利用部分分式法求Y的Z反变换所以,作Z 反变换,......
2023-06-28

5.已知φ=2x,φ=2x-3x是差分方程yx+1+pyx=f的两个特解,求p和f.6.求下列差分方程的通解或在给定条件下的特解:1)yx+2-3yx+1-4yx=0;2)yx+2+4yx+1+4yx=0;3)yx+2-2yx+1+4yx=0;4),.7.已知y=3ex是二阶差分方程yx+2+ayx-1=ex的一个特解,求a.......
2023-11-22

逻辑斯蒂方程是一种在许多领域中都有着广泛应用的数学模型,下面我们通过树的生长过程的例子来说明该模型的建立过程.一棵小树刚栽下去的时候长得比较慢,渐渐地,小树长高了,而且长得越来越快,但长到某一高度后,它的生长速度趋于稳定,然后再慢慢降下来.这一现象具有普遍性.现在我们来建立这种现象的数学模型.如果假设树的生长速度与它目前的高度成正比,则显然不符合两头尤其是后期的生长情形,因为树不可能越长越快;但如......
2023-10-19

GPS系统主要由空间星座、地面监控、用户设备三大部分组成。图252RTK原理2.RTK定义及原理实时动态差分法Real-time kinematic是以载波相位观测量为根据的实时差分GPS测量,它能够实时地提供测站点在指定坐标系中的厘米级精度的三维定位结果。RTK测量系统通常由三部分组成,即GPS信号接收部分、实时数据传输部分和实时数据处理部分。......
2023-06-29
相关推荐