在一元函数中,我们已经知道复合函数的求导公式在求导法中所起的重要作用,对于多元函数来说也是如此.下面我们来学习多元函数的复合函数的求导公式.我们先以二元函数为例,如下所述.一、全导数【知识点回顾】复合函数的求导规则:对于复合函数y=f[φ(x)],设y=f(u),u=φ(x),其中u叫作中间变量.则复合函数求导用公式表示为:即两个可导函数复合而成的复合函数的导数等于函数对中间变量的导数乘上中间变量......
2023-11-20
一、无穷限的广义积分
定义5.3 设函数f(x)在区间[a,+∞)上连续,取b>a,如果极限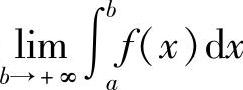 存在,则称此极限值为函数f(x)在无穷区间[a,+∞)上的广义积分,记作
存在,则称此极限值为函数f(x)在无穷区间[a,+∞)上的广义积分,记作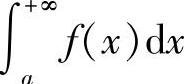 ,即
,即
这时也称广义积分 收敛;反之,则称广义积分
收敛;反之,则称广义积分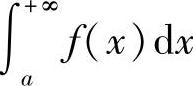 发散.同样,可以定义f(x)在(-∞,b],(-∞,+∞)上的广义积分.
发散.同样,可以定义f(x)在(-∞,b],(-∞,+∞)上的广义积分.
定义5.4 设f(x)在区间(-∞,b]上连续,取a<b,如果极限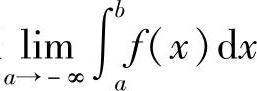 存在,则称此极限值为函数f(x)在无穷区间(-∞,b]上的广义积分,记作
存在,则称此极限值为函数f(x)在无穷区间(-∞,b]上的广义积分,记作 ,即
,即
这时也称广义积分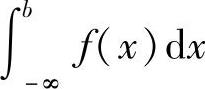 收敛;反之,则称广义积分
收敛;反之,则称广义积分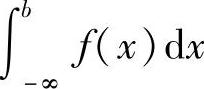 发散.
发散.
定义5.5 设函数f(x)在区间(-∞,+∞)内连续,如果广义积分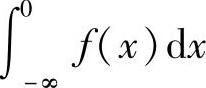 和
和 都收敛,则称上述两个广义积分之和为函数f(x)在无穷区间(-∞,+∞)上的广义积分,记作
都收敛,则称上述两个广义积分之和为函数f(x)在无穷区间(-∞,+∞)上的广义积分,记作 ,即
,即
这时也称广义积分 x收敛;否则,就称广义积分
x收敛;否则,就称广义积分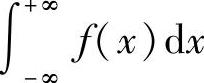 发散.
发散.
设函数f(x)在[a,+∞)上连续,F(x)是f(x)的原函数,为了方便,分别记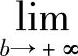 [F(x)]ba为[F(x)]a+∞,
[F(x)]ba为[F(x)]a+∞,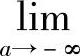 [F(x)]ba为[F(x)]b-∞,则无穷限的广义积分
[F(x)]ba为[F(x)]b-∞,则无穷限的广义积分 ,
,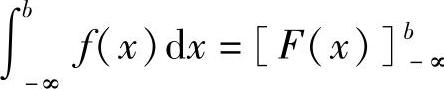 ∞.
∞.
例1 求 ,
,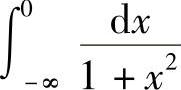 ,
,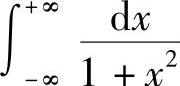 .
.
解 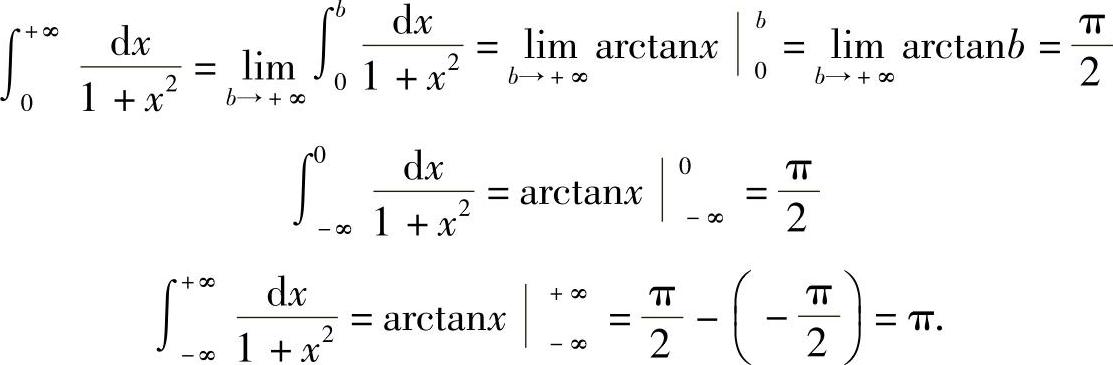
例2 求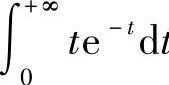 .
.
解 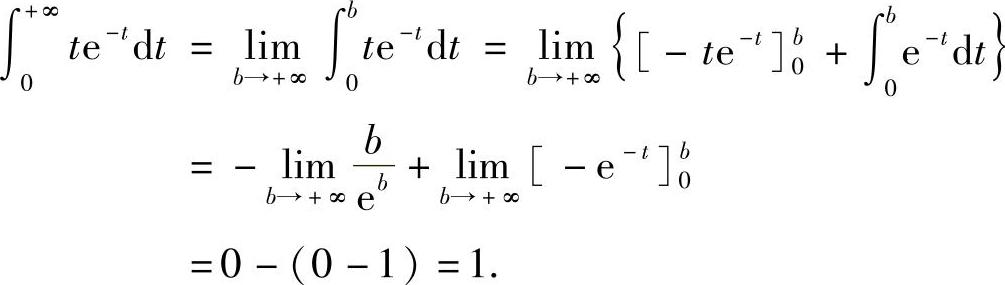
例3 讨论广义积分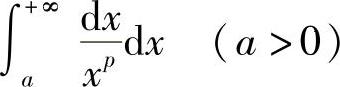 的收敛性.
的收敛性.
解 当p≠1时
又因为当p=1时,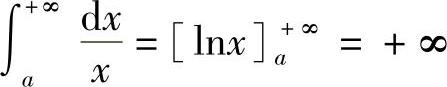 .
.
因此,当p>1时,广义积分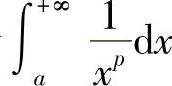 收敛于
收敛于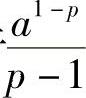 ,当p≤1时,此广义积分发散.二、无界函数的广义积分
,当p≤1时,此广义积分发散.二、无界函数的广义积分
若x0是函数f(x)的无穷间断点,即 ,则x0是f(x)的瑕点.
,则x0是f(x)的瑕点.
定义5.6 设函数f(x)在区间(a,b]上连续,且a为瑕点,取η>0,如果极限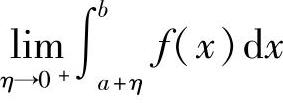 存在,则称此极限值为无界函数f(x)在[a,b]上的广义积分或瑕积分,记作
存在,则称此极限值为无界函数f(x)在[a,b]上的广义积分或瑕积分,记作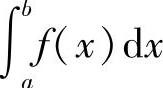 ,即
,即
这时也称广义积分 收敛;若上述极限不存在,则称广义积分
收敛;若上述极限不存在,则称广义积分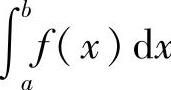 发散.
发散.
当b为瑕点或c∈(a,b)为瑕点时,可类似地定义f(x)在[a,b]上的瑕积分
例4 计算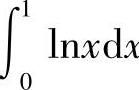 .
.
解 因为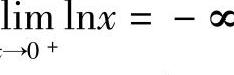 ,所以点x=0是瑕点,(www.chuimin.cn)
,所以点x=0是瑕点,(www.chuimin.cn)
例5 讨论广义积分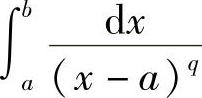 的敛散性(b>a>0,q>0).
的敛散性(b>a>0,q>0).
解 显然点x=a是瑕点,当q≠1时,
当q=1时,
因此,广义积分 ,当q<1时收敛;当q≥1时发散;同样可得,广义积分
,当q<1时收敛;当q≥1时发散;同样可得,广义积分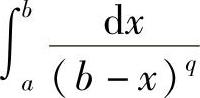 ,当q<1时收敛,当q≥1时发散.三、Γ函数
,当q<1时收敛,当q≥1时发散.三、Γ函数
定义5.7 积分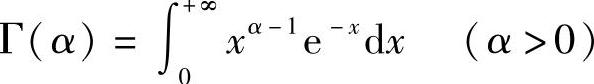 称为Γ函数.
称为Γ函数.
Γ函数有一个重要性质,即递推公式
Γ(α+1)=αΓ(α).
这是因为
特别地
Γ(n+1)=n!
这是因为
Γ(n+1)=nΓ(n)=n(n-1)Γ(n-1)=…=n!Γ(1),又因为
所以
Γ(n+1)=n!
Γ函数还可以写成另一种形式
可以证明
例6 计算 .
.
解 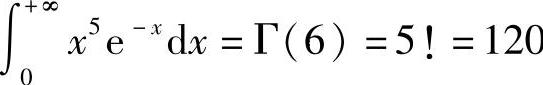 .
.
例7 计算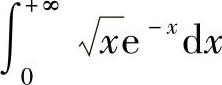
解 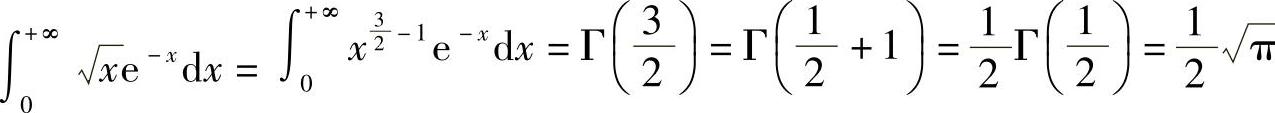 .
.
有关高等数学(上、下册)的文章

在一元函数中,我们已经知道复合函数的求导公式在求导法中所起的重要作用,对于多元函数来说也是如此.下面我们来学习多元函数的复合函数的求导公式.我们先以二元函数为例,如下所述.一、全导数【知识点回顾】复合函数的求导规则:对于复合函数y=f[φ(x)],设y=f(u),u=φ(x),其中u叫作中间变量.则复合函数求导用公式表示为:即两个可导函数复合而成的复合函数的导数等于函数对中间变量的导数乘上中间变量......
2023-11-20

要比较准确地描绘出一般函数的图形,仅用描点作图是不够的,为了提高作图的准确性,可将前面讨论的函数性态应用到曲线的作图上,即先利用函数的一阶、二阶导数,分析函数的单调性、极值、凹凸性与拐点等整体性态,并求出曲线的渐近线,然后再描点作图,称这种作图的方法为分析作图法.其一般步骤如下:(1)确定f(x)的定义域、间断点,并讨论函数的奇偶性、周期性.(2)在定义区间内求函数f(x)的一阶、二阶导数为零或不......
2023-11-19

1)反函数的求导法则求导法则Ⅱ设y=f(x)在区间Ix内单调、可导,且f′(x)≠0,则其函数x=φ(y)在相应的区间Iy内也单调、可导,且证设函数的y=f(x)的反函数x=φ(y)的自变量y的增量为Δy,则相应地x的增量为Δx.由函数可导必连续的性质及反函数的连续性可得,x=φ(y)在区间Iy内单调、连续,因此当Δy→0时,有Δx→0.且当Δy≠0时,有Δx≠0,则y,y+Δy∈Iy,设Δy......
2023-11-19

由于初等函数是由基本初等函数经过有限次四则运算及有限次函数复合而构成的用一个解析式表示的函数,因此结合前面的求导法则与求导公式可推得:初等函数在其定义区间上处处可导,其导函数只要按照函数的结构,利用相应的求导公式或法则就可求出.例10求下列函数的导数:解(1)y′=e2t+t·2e2t=(1+2t)e2t.(2)由于故例11设求F′(x).解当x≠1时,F(x)在相应的定义区间上都是初等函......
2023-11-19

函数f(z)关于闭曲线C的对数留数是指积分这里需要假定函数在C上解析.显然当C为简单正向闭曲线时,上述对数留数就是对数函数Lnf(z)的导数在C内部各个孤立奇点处留数之和.函数f(z)关于简单闭曲线C的对数留数与它在C内部的零点和极点的个数有密切的联系.即定理1 若函数f(z)在正向简单闭曲线C 上解析且没有零点,又在C的内部除有限个极点外解析,则有其中N与P分别是f(z)在C内部零点和极点的总个......
2023-10-30

与狭义水资源不同,广义水资源是在降水通量下定义的水资源量。根据水量平衡原理,地下水资源与地表水资源的不重复量为潜水蒸发量、地下潜流量及开采净消耗量之和,可表示为D,则上式可改写为在降水通量下,R 和D 共同构成了狭义水资源,是对生态环境和人类社会具有效用的水量,属于广义水资源的范畴,因而广义水资源量的确定主要是界定地表蒸发量的有效水分和无效水分。其中河渠、湖泊及水库坑塘的水面蒸发在狭义水资源量中统计。......
2023-10-26
相关推荐