由上一节复积分与实积分的关系式(3.1.2)可以看出,该复积分与路径无关的充要条件是其右端的两个对坐标的曲线积分都与路径无关.而平面上的曲线积分与路径无关的充要条件为:若函数P(x,y)和Q(x,y)在单连通域D内具有一阶连续偏导数,L为D内分段光滑的曲线,则曲线积分在D内与路径无关(或沿D内任意闭曲线的曲线积分为零)的充分必要条件是等式在D内恒成立.对于式右端的两个曲线积分,上述条件等式应当分别......
2025-09-30
一、定积分的元素法
从前面讨论过的曲边梯形的面积和变速直线运动的路程可以看出,定积分所解决的问题可归结为求与区间[a,b]上有关的量A,解决问题的步骤是:分割——近似代替——求和——取极限.这里的整体量A对于区间[a,b]具有可加性,即若把[a,b]分成若干个小区间[xi-1,xi](i=1,2,…,n),就有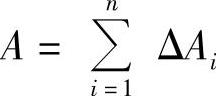 ,其中ΔAi是对应于小区间[xi-1,xi]的局部量;可以近似地求出ΔAi,即ΔAi≈f(ξi)Δxi(i=1,2,…,n),这里f(x)是已知函数,ξi∈[xi-1,xi](i=1,2,…,n),并且满足:ΔAi-f(ξi)Δxi是比Δxi更高阶的无穷小量(当Δxi→0时),则A可以表示为定积分
,其中ΔAi是对应于小区间[xi-1,xi]的局部量;可以近似地求出ΔAi,即ΔAi≈f(ξi)Δxi(i=1,2,…,n),这里f(x)是已知函数,ξi∈[xi-1,xi](i=1,2,…,n),并且满足:ΔAi-f(ξi)Δxi是比Δxi更高阶的无穷小量(当Δxi→0时),则A可以表示为定积分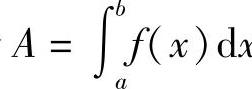 .
.
如果实际问题中的所求量A符合下列条件:
1)A是与一个变量的变化区间[a,b]有关的量;
2)A对于区间[a,b]具有可加性;
3)局部量ΔAi的近似值可表示为f(ξi)Δxi,这里f(x)是实际问题选择的函数.则该实际问题可以用定积分来解决.
解决步骤如下.
第一步:分割区间,写出微元.
分割区间[a,b],取具有代表性的任意一个小区间(不必写出下标号),记作[x,x+dx],设相应的局部量为ΔA,分析局部量ΔA,选择函数f(x),写出近似等式
ΔA≈dA=f(x)dx.
第二步:求定积分得整体量.
令Δx→0,对这些微元求和后取极限,得到的定积分就是所要求的整体量
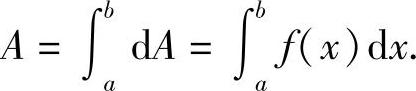
上述方法称为定积分的元素法,又称微元法.
二、平面图形的面积
根据定积分几何意义,由曲线y=f(x)(f(x)≥0)和直线x=a,x=b以及y=0所围成的曲边梯形的面积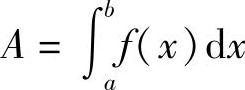 ;
;
由在区间[a,b]上的连续曲线y=f(x)(有的部分为正,有的部分为负),x轴及直线x=a与x=b所围成的平面图形的面积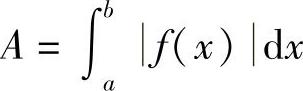 ;
;
如果平面区域是由区间[a,b]上的两条连续曲线y=f(x)与y=g(x)及直线x=a与x=b围成(见图5-5a),则它的面积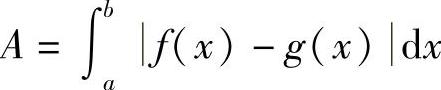 ;
;
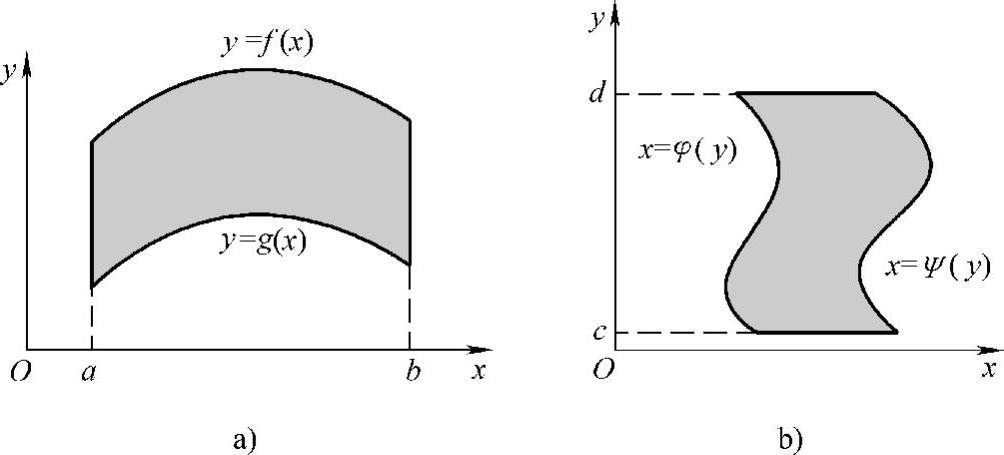
图5-5
如果平面区域是由区间[c,d]上的两条连续曲线x=φ(y)与x=Ψ(y)及直线y=c与y=d围成(见图5-5b),则它的面积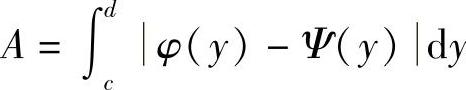 .
.
例1 求由y=lnx,x轴及直线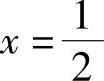 与x=2所围成的平面图形的面积(见图5-6).
与x=2所围成的平面图形的面积(见图5-6).
解 已知在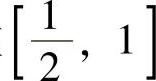 上,lnx≤0,在[1,2]上,lnx≥0
上,lnx≤0,在[1,2]上,lnx≥0
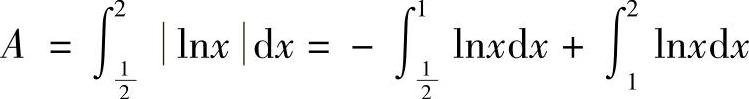
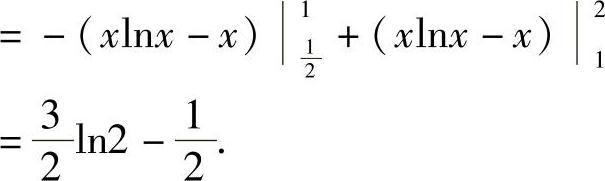
例2 求抛物线y2=2x和直线y=-x+4所围成的图形的面积(见图5-7).
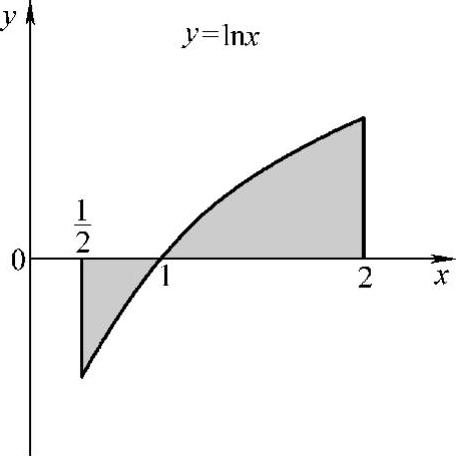
图5-6
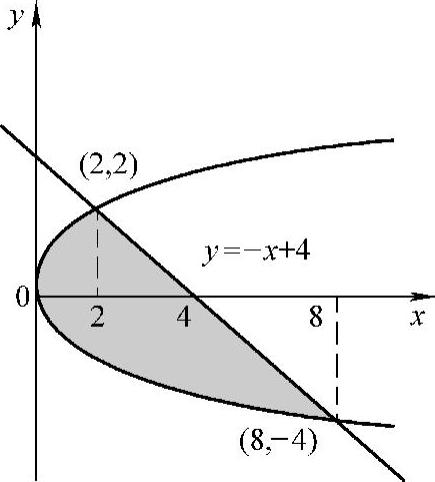
图5-7
解 先求抛物线和直线的交点,解方程组
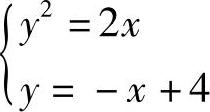
解得交点为(2,2)和(8,-4).
方法一:选x为积分变量,变化区间为[0,8],面积为
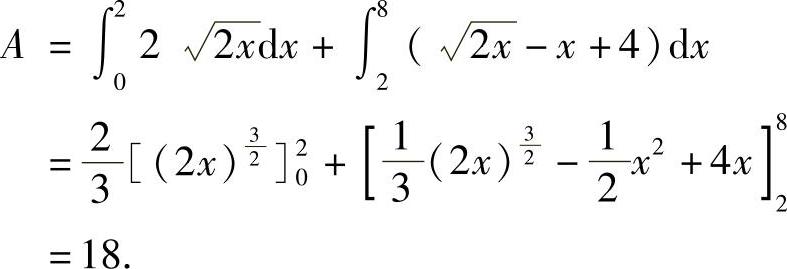
方法二:选y作积分变量,则y的变化区间为[-4,2],所求的面积为
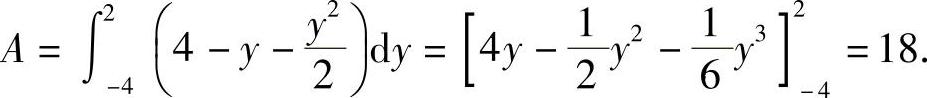
由本例题可以看出,选择适当的变量可以使计算更加简便.
例3 求椭圆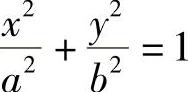 所围成的面积.
所围成的面积.
解 此椭圆关于两个坐标轴都对称(见图5-8),故只需求它在第Ⅰ象限内的面积A1,则椭圆的面积为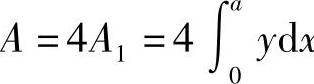 .
.
利用椭圆的参数方程
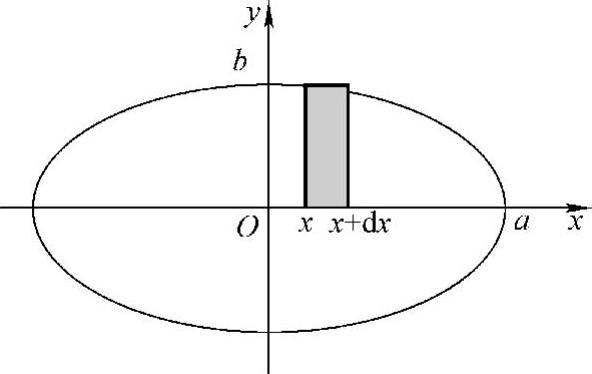
图5-8
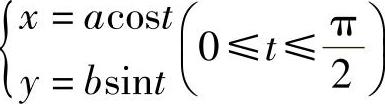
令x=acost,则y=bsint,dx=-asintdt
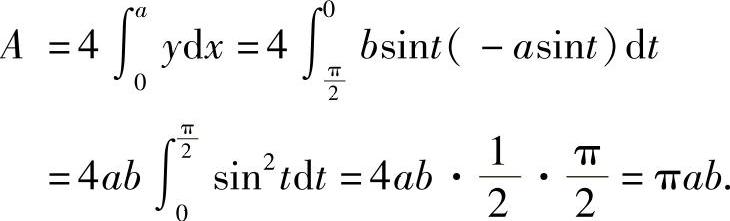
当a=b时,就得到圆的面积公式A=πa2.
本例题中,参数方程所确定的函数的积分,实质是作了一次变量代换.
三、两种特殊立体的体积
1.平行截面面积为已知函数的立体的体积
设空间某立体是由一曲面和垂直于x轴的平面x=a和x=b围成(见图5-9)的,如果用过任意点x(a≤x≤b)且垂直于x轴的平面截立体所得到的截面面积是已知连续函数
S(x)(a≤x≤b),则此立体的体积为
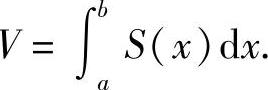
例4 已知两个底半径为R的圆柱体垂直相交,求它们公共部分的体积.
解 如图5-10所示,公共部分的体积为阴影部分体积的8倍,现考虑阴影部分体积.任意一个垂直于x轴的截面都为正方形,其边长为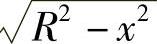 ,因此截面面积为S(x)=R2-x2
,因此截面面积为S(x)=R2-x2
所以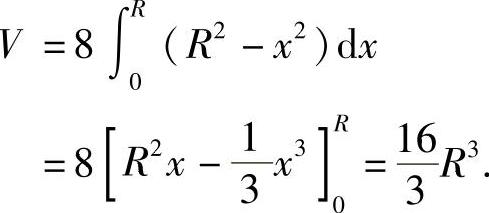
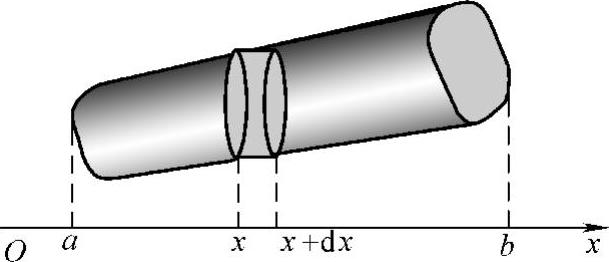
图5-9
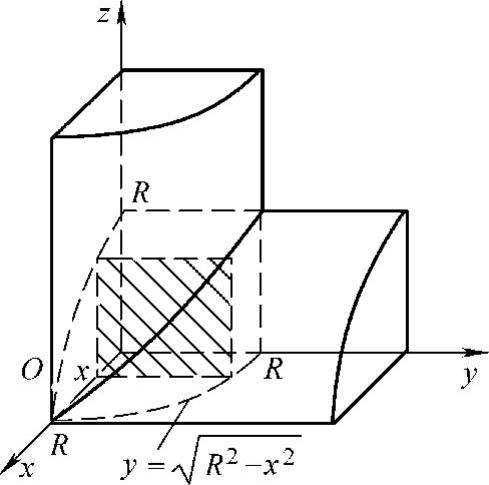
图5-10
2.旋转体的体积
由连续曲线y=f(x)(x≥0)与直线x=a,x=b及x轴所围成的曲边梯形绕x轴旋转,所得的立体叫做旋转体(见图5-11)显然过点x(a≤x≤b)且垂直于x轴的截面是以f(x)为半径的圆,其面积是S(x)=πf2(x),于是得旋转体的体积为
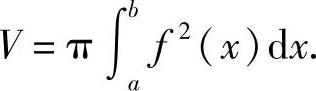
类似地,由连续曲线x=φ(y)和直线y=c,y=d及y轴所围成曲边梯形绕y轴旋转所生成的旋转体的体积为
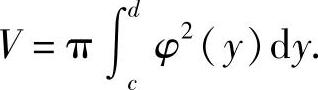
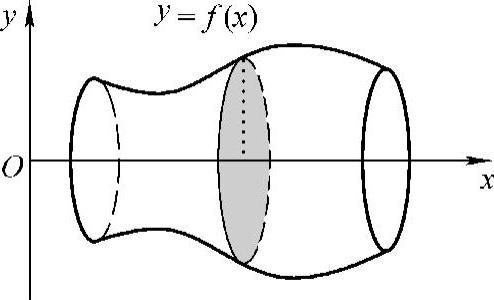
图5-11
例5 求椭圆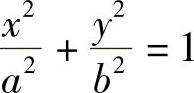 分别绕x轴和y轴旋转所得旋转体的体积.
分别绕x轴和y轴旋转所得旋转体的体积.
解 (1)绕x轴旋转
这个旋转体是由半个椭圆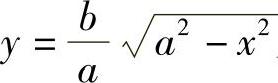 及x轴围成的图形绕x轴旋转而成的立体,所以
及x轴围成的图形绕x轴旋转而成的立体,所以
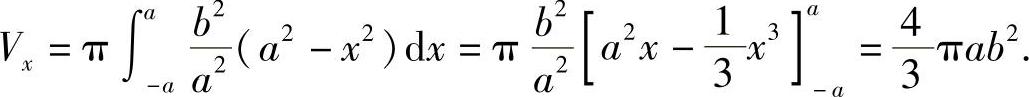
(2)绕y轴旋转
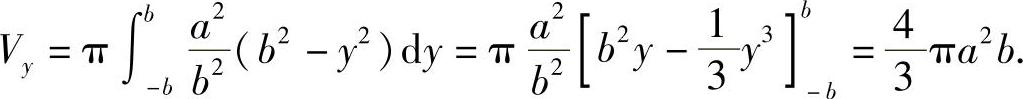
当a=b时,得半径为a的球体的体积: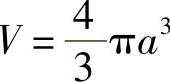 .
.
例6 求由圆(x-b)2+y2=a2(0<a<b)绕y轴旋转一周得到的旋转体的体积.
解 将圆的方程改写为
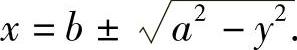
如图5-12所示,右半圆的方程是
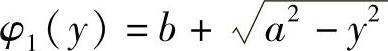
左半圆的方程是
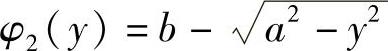
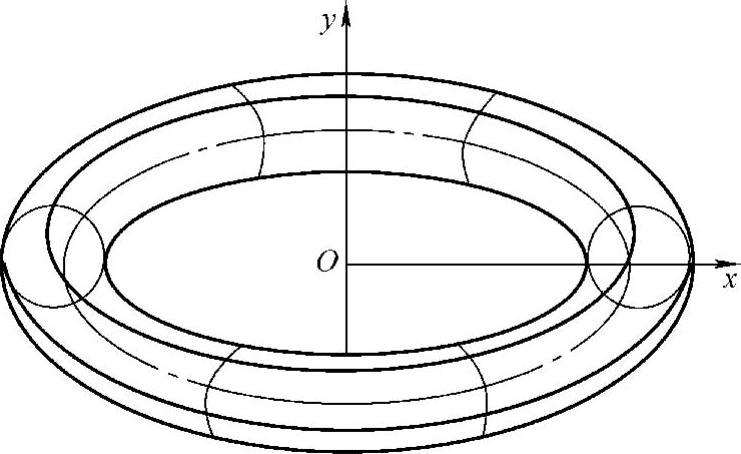
图5-12
所求的旋转体(环体)的体积是分别以两个半圆为曲边的曲边梯形绕y轴旋转一周所得的旋转体的体积的差,即
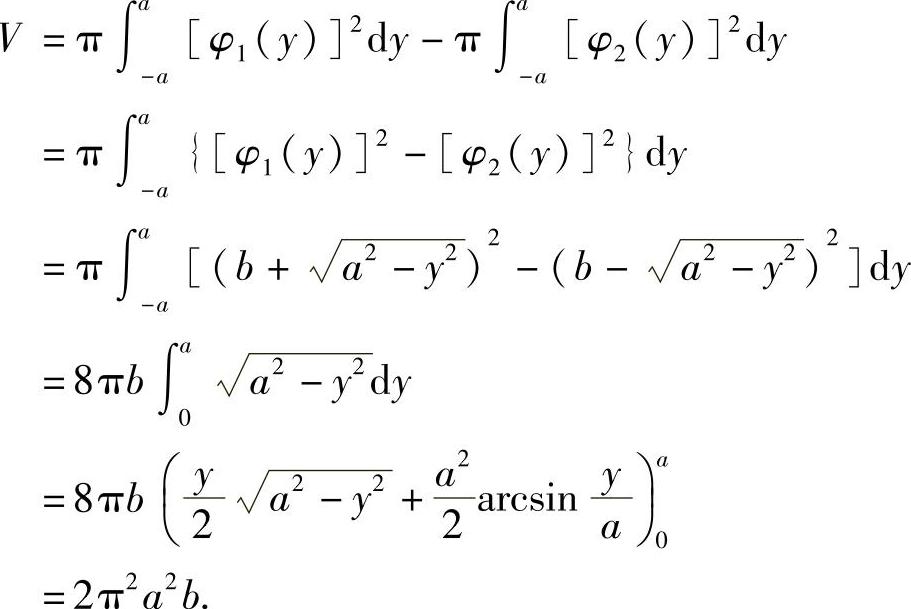
四、平面曲线的弧长
由于平面上的光滑曲线弧是可求长的,故可用定积分来计算弧长.
1.直角坐标情形
已知曲线弧在直角坐标系下的方程为
y=f(x)(a≤x≤b),
其中,f(x)在[a,b]上有一阶连续导数.下面求该曲线弧的长度.
取x为积分变量,积分区间为[a,b],在[a,b]上任取一个小区间[x,x+dx],则弧微分公式为
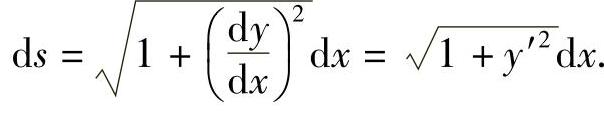
故所求弧长为
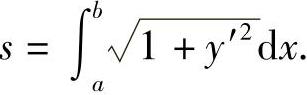
如果曲线弧的方程为x=φ(y)(c≤y≤d),且φ(y)在[c,d]上有一阶连续导数.则取y为积分变量,积分区间为[c,d],则弧微分公式为
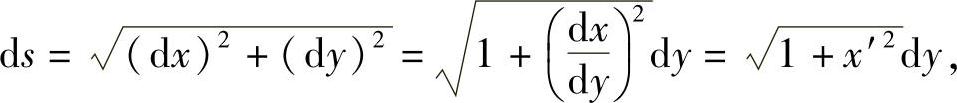
故所求弧长为
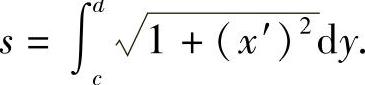
例7 求曲线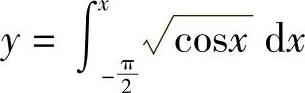 的弧长.
的弧长.
解 因为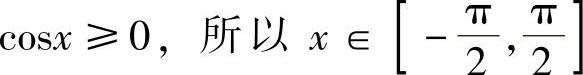 .取x为积分变量,积分区间为
.取x为积分变量,积分区间为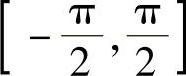 ,则弧长元素为
,则弧长元素为
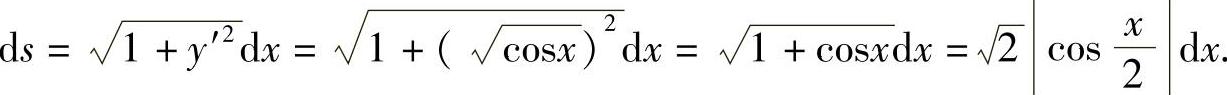
故所求弧长
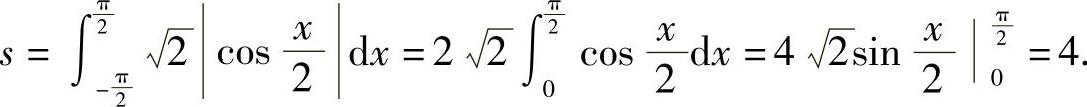 (https://www.chuimin.cn)
(https://www.chuimin.cn)
2.参数方程情形
已知曲线弧的参数方程为
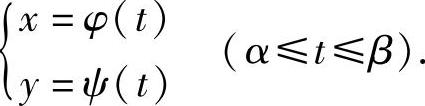
其中,φ(t),ψ(t)在[α,β]上有连续导数,求该曲线的弧长.
取参数t为积分变量.则积分区间为[α,β],则弧微分公式为
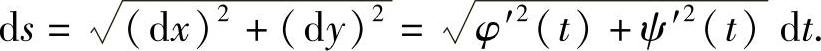
故所求弧长
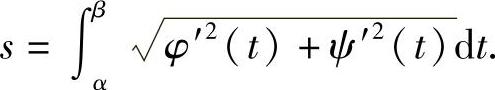
例8 求曲线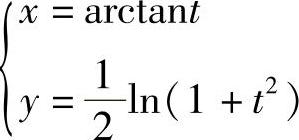 自t=0到t=1的一段弧的弧长.
自t=0到t=1的一段弧的弧长.
解 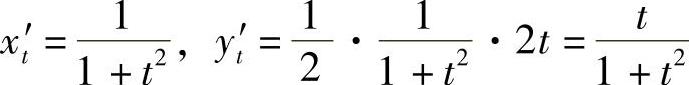 ,则弧长元素
,则弧长元素
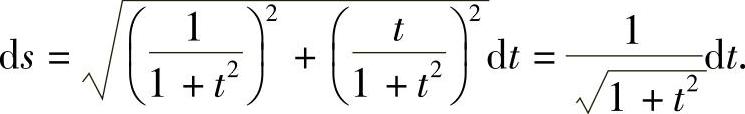
故所求弧长
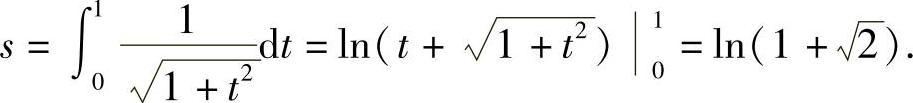
3.极坐标情形
已知曲线弧的极坐标方程为
r=r(θ)(α≤θ≤β).
其中,r(θ)在[α,β]上有连续导数,求该曲线弧的弧长.
由直角坐标与极坐标的关系
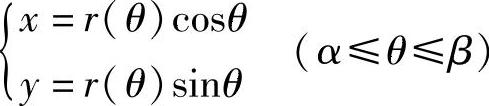
将θ看成参数,则弧长元素
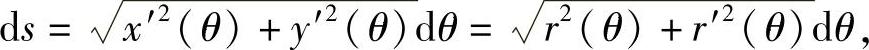
故所求弧长为
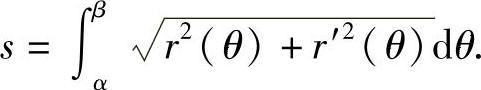
例9 求曲线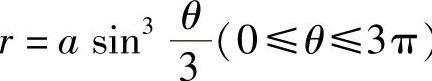 )的长度.
)的长度.
解 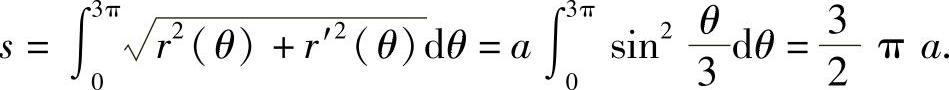
五、定积分在物理学上的应用
1.变力沿直线所做的功
常力沿直线所做的功已有公式可求,如果物体在运动过程中所受到的力是变化的,计算这种变力做功又如何计算呢?
例10 在底面积为S的圆柱形容器中盛有一定量的气体.在等温条件下,由于气体的膨胀,把容器中的一个活塞(横截面积为S)从点a处推移到点b处.计算在移动过程中,气体压力所做的功.
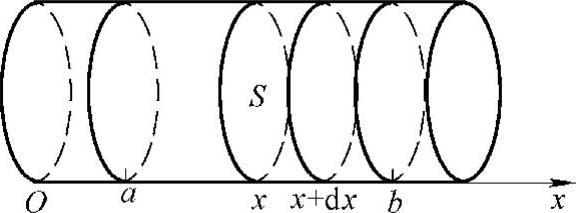
图5-13
解 取坐标系如图5-13所示,活塞的位置可以用坐标x来表示.由物理学知道,一定量的气体在等温条件下,压强p与体积V的乘积是常数k,即
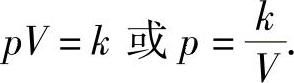
在点x处,因为V=xS所以作用在活塞上的力为
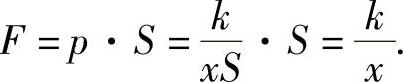
取x为积分变量,变化区间为[a,b].当活塞从x移动到x+dx时,变力所做的功近似为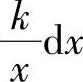 ,即功元素为
,即功元素为
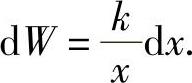
于是所求的功为
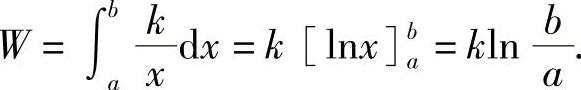
例11 设重度为10(kN/m3)、半径为r(m)的球浸在水中,且与水面相接,为将球从水中取出,需做多少功?
解 如图5-14所示建立坐标系,则球的方程为x2+y2=r2,把球从水中取出,相当于把每一水平薄层提高2r,在提高2r时,所做的功分为两个过程:
1)将薄层提升至水面,因为球的重度为10(kN/m3),与水的重度相等,所以提升力为零,即不做功.
2)将薄层由水面提升到r+y处,提升力为此薄层的重力
dW=γπx2dy=10π(r2-y2)(r+y)dy
故需做功为
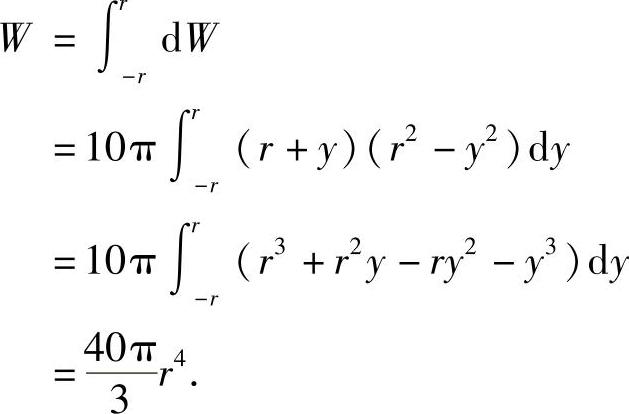
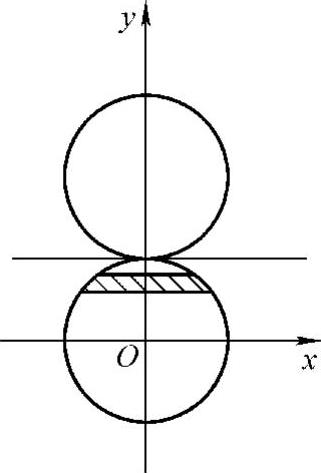
图5-14
2.水压力
从物理学知道,在水深为h处的压强为p=ρgh,这里ρ是水的密度.如果有一面积为A的平板水平地放置在水深为h处,那么平板一侧所受的水的压力为
P=p·A.
如果将这个平板铅直放置在水中,那么由于水深不同的点处压强p不相等,所以平板所受水的压力就不能用上述方法计算.
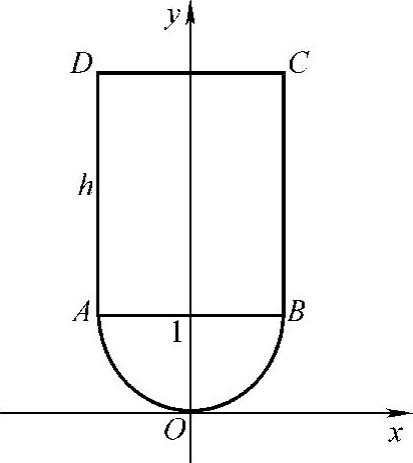
图5-15
例12 某闸门的形状与大小如图5-15所示,闸门的上部为矩形,下部为二次抛物线,当水面与闸门的上端相平时,欲使闸门矩形部分承受的压力与闸门的下部承受的压力之比为5∶4,问闸门矩形部分的高应是多少?
解 如图5-15所示,建立坐标系,则抛物线方程为y=x2,闸门矩形部分承受的压力为
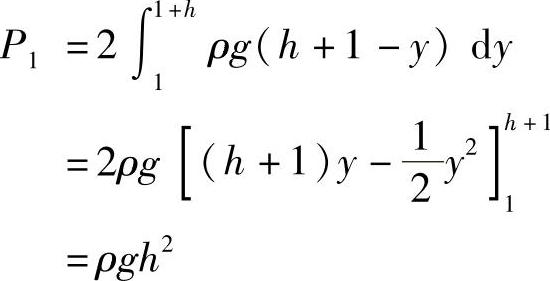
其中,ρ是水的密度,g是重力加速度,闸门的下部承受的压力为
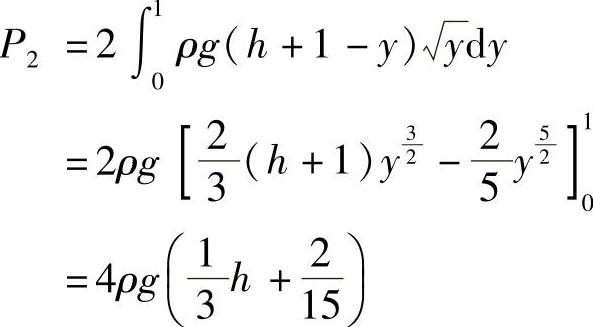
由题意知
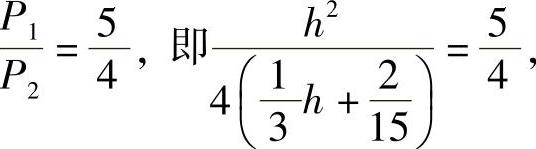
得h=2,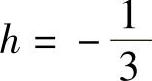 (舍).
(舍).
故h=2,即闸门矩形部分的高为2m.
3.引力
从物理学知道,质量分别为m1、m2,相距为r的两质点间的引力的大小为
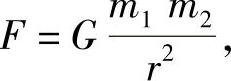
其中,G为引力系数,引力的方向沿着两质点连线方向.
如果要计算一根细棒对一个质点的引力,那么,由于细棒上各点与该质点的距离是变化的,且各点对该质点的引力的方向也是变化的,就不能用上述公式来计算.
例13 设有一长度为l、线密度为ρ的均匀细直棒,在其中垂线上距棒a单位处有一质量为m的质点M,试计算该棒对质点M的引力.
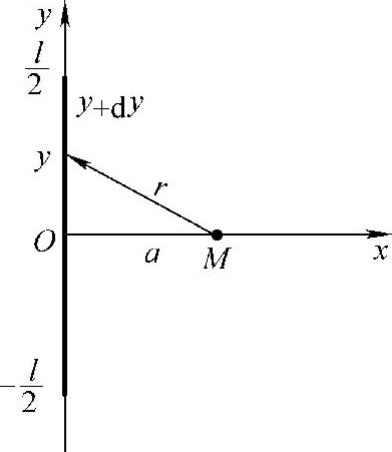
图5-16
解 取坐标系如图5-16所示,使棒位于y轴上,质点M位于x轴上,棒的中点为原点O.由对称性知,引力在垂直方向上的分量为零,所以只需求引力在水平方向的分量.取y为积分变量,它的变化区间为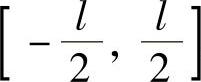 .在
.在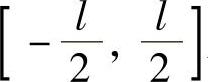 上的y点取长为dy的一小段,其质量为ρdy,与M相距
上的y点取长为dy的一小段,其质量为ρdy,与M相距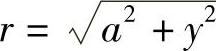 .于是在水平方向上,引力元素为
.于是在水平方向上,引力元素为
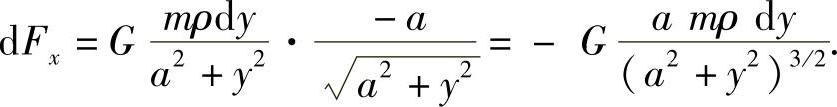
引力在水平方向的分量为
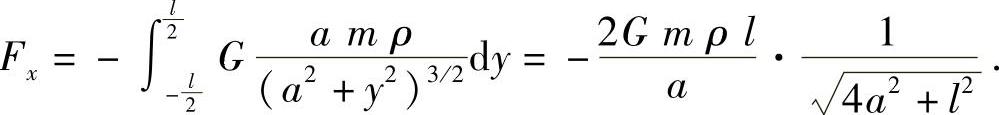
六、定积分在经济学中的应用
首先介绍几个相关概念.
已知某产品在时刻t的总产量的变化率为f(t),则从时刻t1到时刻t2的总产量为
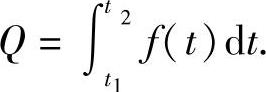
已知边际成本C′(x)是产品的产量x的函数,则生产第x个单位产品的总成本为
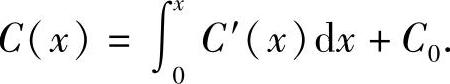
已知总费用变化率f(x),其中,x是变量,则总费用为
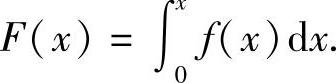
已知某种新产品投入市场的销售速度为时间t的函数f(t),那么,在T个单位时间内,该产品的总销售量为
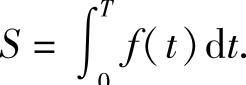
已知某产品产量为x时的边际收益为R′(x),总收益为R(x),销售量为x的平均收益为R(x),则
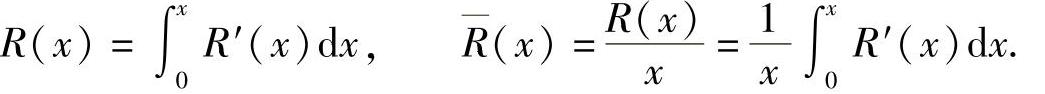
例14 已知某商品每周生产x单位时,总费用的变化率是f(x)=0.4x-12(元/单位),求总费用F(x);如果这种产品的销售单价是20(元),求总利润L(x),并问每周生产多少单位时才能获得最大利润?
解 总费用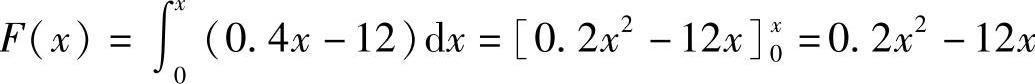 ,
,
销售x单位商品得到的总收入为R(x)=20x.
又因为总利润L(x)=R(x)-F(x),
所以
L(x)=20x-(0.2x2-12x)=32x-0.2x2.
令L′(x)=0,
即32-0.4x=0,得x=80,因此最大利润为
L(80)=32×80-0.2×802=1280(元).
例15 已知某产品的边际成本为C′(x)=2x2-3x+2(元/单位),求:
1)生产前6个单位产品的可变成本;
2)若固定成本C(0)=6(元),求前6个产品的平均成本;
3)求生产第10个到第15个单位产品时的平均成本.
解 1)生产前6个单位产品,即从生产第1个到第6个单位的可变成本为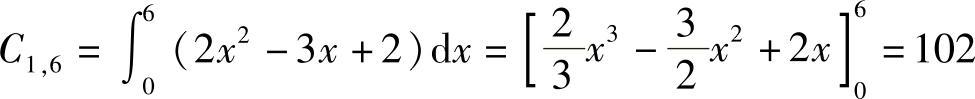 (元).
(元).
2)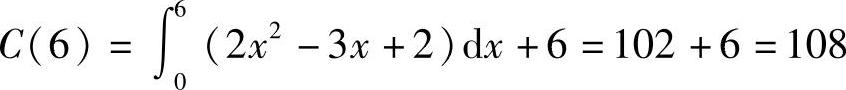 .
.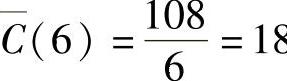 8(元/单位).
8(元/单位).
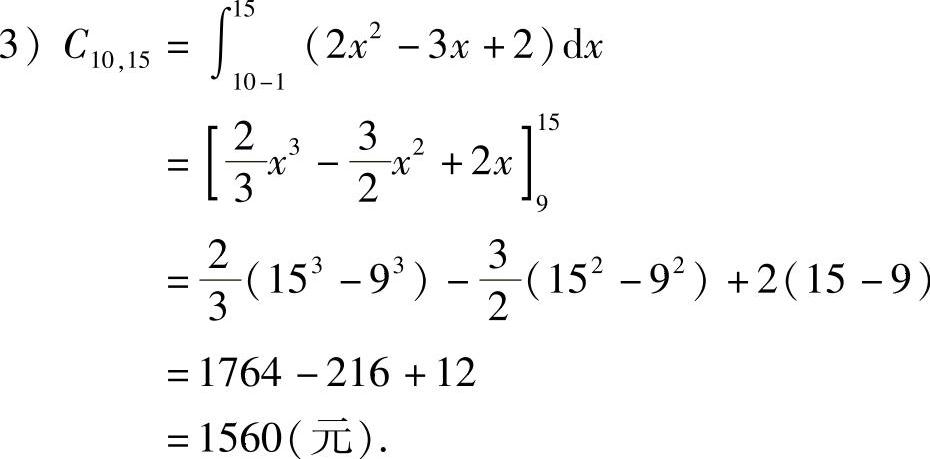
相关文章

由上一节复积分与实积分的关系式(3.1.2)可以看出,该复积分与路径无关的充要条件是其右端的两个对坐标的曲线积分都与路径无关.而平面上的曲线积分与路径无关的充要条件为:若函数P(x,y)和Q(x,y)在单连通域D内具有一阶连续偏导数,L为D内分段光滑的曲线,则曲线积分在D内与路径无关(或沿D内任意闭曲线的曲线积分为零)的充分必要条件是等式在D内恒成立.对于式右端的两个曲线积分,上述条件等式应当分别......
2025-09-30

设D为一单连通域,z0为D中的一点.若f(z)在D内解析,那么函数在z0点不解析.下面考虑D内围绕z0的简单闭曲线C上积分的计算.根据闭路变形原理,该积分值等于沿任何一条围绕z0的简单闭曲线上的积分.既然沿围绕z0的任何简单闭曲线积分值都相同.那么我们就取以z0为中心,半径为δ的圆周|z-z0| = δ(取其正向)作为积分曲线C.由于f(z)的连续性,在C上的函数f(z)的值将随着δ的缩小而逐渐接......
2025-09-30

逻辑学中,概念的定义就是给概念下定义,定义的对象就是概念。(五)操作定义通过对一整套相关的操作程序的描述来给概念下定义。这就是对“水”概念的合取定义。这是析取定义,满足其中之一,即符合“湿地”概念,或者可以判定为湿地。对于属加种差定义,除了最大、最外、最上的概念无法定义以外,最初始的概念也无法定义。(一)穷举定义如果一个概念外延集合内的对象很少,或者其种类有限,就可以对它下穷举的外延定义。......
2025-09-30

极限是微积分学中一个基本概念,微分学与积分学的许多概念都是由极限引入的,并且最终由极限知识来解决.因此它在微积分学中占有非常重要的地位.我国春秋战国时期的《庄子·天下篇》中说:“一尺之棰,日取其半,万世不竭”,这就是极限的最朴素思想.一、数列极限的定义(一)数列的概念定义1按自然数顺序递增的一列数称为数列.即简记为:{un}.数列中的每一个数称为数列的项,其中第一项u1称为数列的首项,第n项称为......
2025-09-30

定理2 设f(z)在实轴上解析,在上半平面Imz >0除有限个奇点z1,z2,··· ,zn 外解析.若存在正数r,M 和α >1,使当|z| ≥r 且Imz ≥0 时f(z)解析且满足|f(z)|≤M/|z|α,则积分I2 =存在且有证明设CR为上半圆周z = Reiθ(0 ≤θ ≤π),取充分大的R 使R ≥r并且奇点z1,z2,··· ,zn均在由CR及实轴上从-R 到R 的一段所围成的闭路......
2025-09-30

定理1(傅氏积分定理) 若函数f(x)在(-∞,+∞)内有定义,且满足(1)在任一有限区间上满足狄利克雷条件,即在任意区间内满足: 连续或只有有限个第一类间断点; 只有有限个极值点;(2)在无限区间(-∞,+∞)内绝对可积(即积分收敛),则在f(x)的连续点上有成立,而左端的f(t)在它的间断点t处,应以来代替.这个定理称为傅里叶积分定理,简称为傅氏积分定理,其中所列的条件是充分的,它的证明需要用......
2025-09-30

复变函数的定义在形式上与一元实函数一样,只是将自变量和因变量都推广到了复数域.定义1 设D为复平面上的非空集合[1],若有一个确定的法则存在,按照这一法则,对于D 内的每一个复数z =x+iy,都有确定的复数w =u+iv 与之对应,我们称复变数w是z的复变函数,记为w =f(z).其中z称为自变量,w为因变量,集合D称为w = f(z)的定义域,与D 中所有复数z对应的w值的集合G 称为w =f......
2025-09-30

【主要内容】1.积分中值定理设函数f(x)在[a,b]上连续,则存在ξ∈[a,b],使得注 (ⅰ)当上述的f(x)是单调函数时,中值ξ∈(a,b).(ⅱ)积分中值定理具有以下的推广形式:设函数f(x)在[a,b]上连续,函数g(x)在[a,b]上可积且不变号,则存在ξ∈[a,b],使得2.积分中值定理的应用积分中值定理主要用于把抽象函数f(x)的定积分转换成f(x)在[a,b]上某点η处的值与(b......
2025-09-30
相关推荐