一、原函数与不定积分定义4.1 设f（x）是定义在区间I上的函数，如果存在函数F（x），对于任意x∈I，都有F′（x）=f（x）或dF（x）=f（x）dx则称函数F（x）为函数f（x）在区间I上的一个原函数.例如，因为（sinx）′=cosx，则sinx是cosx的原函数.又因为（sinx+1）′=cosx，所以sinx+1也是cosx的原函数.由此例可以看出，一个函数若有原函数，则原函数可以不止......
2023-11-22
高等数学：定积分的概念和性质
【摘要】：一、引例1.曲边梯形的面积设函数y=f（x）在闭区间[a，b]上非负且连续，则曲线y=f（x）与直线x=a，x=b，y=0围成的图形（见图5-1）称为曲边梯形.求其面积A的基本思想是在很小的区间上用小矩形面积近似代替小梯形面积.图5-1第一步：分割.用一串分点a=x0＜x1＜…
一、引例
1.曲边梯形的面积
设函数y=f（x）在闭区间[a，b]上非负且连续，则曲线y=f（x）与直线x=a，x=b，y=0围成的图形（见图5-1）称为曲边梯形.求其面积A的基本思想是在很小的区间上用小矩形面积近似代替小梯形面积.
图5-1
第一步：分割.
用一串分点a=x0＜x1＜…＜xn=b，把[a，b]分成n个小区间，过每个分点作x轴的垂线段，相应地把曲边梯形分成n个小曲边梯形，其中，第i个小曲边梯形为
xi-1≤x≤xi，0≤y≤f（x），记它们的面积依次为
ΔA1，ΔA2，…，ΔAn.
第二步：取近似.
在每个小区间[xi-1，xi]上任取一点ξi，以区间[xi-1，xi]的长为底，f（ξi）为高的小矩形的面积应为第i个小曲边梯形面积的近似值，即
ΔAi≈f（ξi）Δxi.
第三步：作和.
将n个小矩形的面积相加，得到曲边梯形面积A的近似值，即
第四步：求极限（由近似过渡到精确）.
显然上述过程划分得越细，近似效果越好，为保证每个小区间的长度都无限小，记
于是，令λ→0（这时小区间的个数n无限增多，即n→∞），如果上述和式极限存在，则此极限值就是曲边梯形的面积，即
2.变速直线运动的路程问题
设物体作变速直线运动，其速度v是时间t的函数v=v（t），下面计算该物体从时刻a到时刻b经过的路程s.
第一步：分割.
用一串分点a=t0＜t1＜…＜tn=b，把[a，b]分成n个小区间[tj-1，tj]，小区间长度记为Δtj=tj-tj-1（j=1，2，…，n），各时间段内物体运动的路程依次为
Δs1，Δs2，…，Δsn.
第二步：取近似.
在[tj-1，tj]上任取一点τj，以时刻τj的速度v（τj）近似代替[tj-1，tj]上的速度，则在Δtj时间内物体经过的路程Δsj的近似值为
Δsj≈v（τj）Δtj.
第三步：作和.
将n个时间段的路程近似值相加，便得到总路程s的近似值：
第四步：求极限.
记
，令λ→0，如果上述和式极限存在，则此极限值就是总路程s
的精确值，
即
二、定积分的定义
上面的两个例子，前者是几何量，后者为物理量，虽然问题不同但解决的方法是相同的，都是通过“分割、近似、作和、求极限”这四个步骤化为具有同一数学结构的和式极限.抛开问题的实际意义，保留其数学结构，便可抽象出定积分的概念.
定义5.1 设f（x）在区间[a，b]有定义，在[a，b]内任意插入n-1个分点：a=x0＜x1＜x2＜…＜xn-1＜xn=b，将[a，b]分成n个小区间：[x0，x1]，[x1，x2]，…，[xi-1，xi]，…，[xn-1，xn]，第i个小区间[xi-1，xi]的长度表示为Δxi=xi-xi-1，记λ1=≤im≤nax{Δxi}在[xi-1，xi]中任取一点ξi（i=1，2，3，…，n），作和
f（ξi）Δxi.如果当λ→0时，S趋于确定的极限I，且I与分法无关，也与ξi在[xi-1，xi]中的取法无关，则称f（x）在[a，b]上可积，极限I称为f（x）在[a，b]上的定积分，记作∫baf（x）dx，即
其中，f（x）叫做被积函数，f（x）dx叫做被积表达式，x叫做积分变量，a与b叫做积分下限与积分上限.
如果当λ→0时，积分和S不存在极限，则称f（x）在[a，b]上不可积.
注：1）定积分的值只与被积函数f（x）以及积分区间[a，b]有关，而与积分变量用什么字母表示无关，即
2）被积函数f（x）在区间[a，b]上有界只是可积的必要条件，关于可积的充分条件只给出如下三个结论，而不作深入研究.
定理5.1 若函数f（x）在区间[a，b]上连续，则f（x）在区间[a，b]上可积.
定理5.2 若函数f（x）在区间[a，b]上有界，且只有有限个间断点，则f（x）在区间[a，b]上可积.
定理5.3 若函数f（x）在区间[a，b]上是单调的，则f（x）在区间[a，b]上可积.
3）为计算和使用方便，作如下规定：
规定1 当a=b时，∫baf（x）dx=∫aaf（x）dx=0；
规定2 当a＞b时，∫baf（x）dx=-∫abf（x）dx.
4）根据定积分的定义，前面两个引例中，曲边梯形的面积A用定积分可表示为
A=∫baf（x）dx.变速直线运动的路程s用定积分可表示为
s=∫bav（x）dx.三、定积分的几何意义
若在[a，b]上，f（x）≥0，则定积分∫baf（x）dx表示由曲线y=f（x），x轴及直线x=a，x=b所围成的曲边梯形的面积.
若f（x）≤0，则定积分∫baf（x）dx表示上述曲边梯形的面积的相反数.
若函数f（x）在[a，b]上有正有负，则定积分∫baf（x）dx表示各部分面积的代数和.如图5-2所示.
图5-2
例1 计算定积分
.
解 由定积分的几何意义知，该积分值等于由x=0，x=a，y=0和y=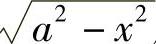
所围半径为a的四分之一圆的面积，
即(www.chuimin.cn)
例2 计算定积分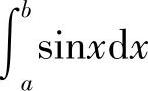
解 因为f（x）=sinx在[a，b]上连续，故sinx在[a，b]上可积，因此可以对[a，b]采用特殊的分法，以及选取特殊的点ξi，取极限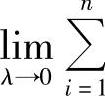
f（ξi）Δxi，即得到积分值.
将[a，b]n等分，则
，取
，i=1，2，…，n则有
为了书写方便，令
，利用积化和差公式有
所以
四、定积分的基本性质
在下面讨论中，总假设函数在所讨论的区间上都是可积的.
性质1 ∫ba[f（x）±g（x）]dx=∫baf（x）dx±∫bag（x）dx.
证 
性质2 
（k为常数）.
性质3（积分区间的可加性） 如果将积分区间分成两部分，则在整个区间上的定积分等于这两部分区间上定积分之和，设a＜c＜b，则
证 因为函数f（x）在[a，b]上可积，所以不论把[a，b]怎样划分，也不论ξi怎样选取，当λ→0时，积分和的极限都是不变的，所以可以选取c（a＜c＜b）永远是个分点
即
推广 不论a，b，c的相对位置如何，总有等式
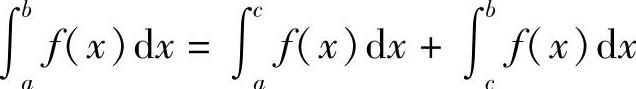
成立.例如，当a＜b＜c时，由于
则
性质4 如果在闭区间[a，b]上f（x）≡1，则
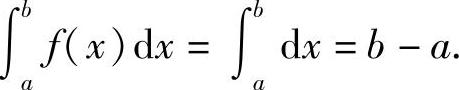
性质5 如果在闭区间[a，b]上f（x）≥0，则
证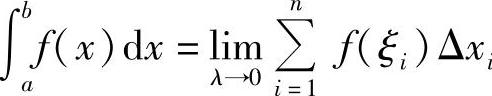 
.
因为f（x）≥0，故f（ξi）≥0（i=1，2，…，n），又因为Δxi≥0（i=1，2，…，n），因此
所以
即
推论5.1 如果在闭区间[a，b]上，f（x）≤g（x），则
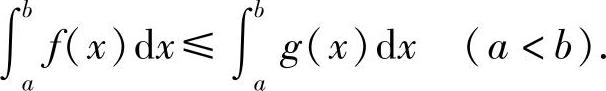
推论5.2 
性质6 设M和m分别是函数f（x）在闭区间[a，b]上的最大值和最小值，则
证 因为m≤f（x）≤M，由推论5.1得
再由性质2及性质4可得
性质7 如果函数f（x）在闭区间[a，b]上连续，则在积分区间[a，b]上至少存在一点ξ，使下式成立
证 因f（x）在[a，b]上连续，故必存在最大值M与最小值m，由性质6，有
这说明，
介于M与m之间，根据闭区间上连续函数的介值定理（第一章第七节定理1.22），在区间[a，b]内存在一点ξ，使得函数f（x）在点ξ处的值与这个值相等，
即
此性质称为积分中值定理
积分中值定理有其明显的几何意义：
设f（x）≥0，由曲线y=f（x），x轴及直线x=a，x=b所围成的曲边梯形的面积等于以区间[a，b]为底，某一函数值f（ξ）为高的矩形面积（见图5-3）.
称为函数f（x）在区间[a，b]上的平均值.
图5-3
有关高等数学（上、下册）的文章
- 详细阅读
- 详细阅读
- 详细阅读
-
高等数学上册：不定积分性质总结详细阅读
性质1设函数f（x）的原函数存在，k为非零常数，则证因为，所以类似可证明不定积分有下列性质.性质2设函数f（x）与g（x）的原函数均存在，则性质2可推广到有限个函数的情形.利用不定积分的性质和基本积分公式可以求一些简单函数的不定积分.对于不定积分运算需要指出，虽然每个积分号都含有任意常数，但任意常数之和仍是任意常数，所以遇到几个任意常数时只要写一个任意常数即可.例5求解例6求解积分运......
2023-11-19
-
高等数学基础：不定积分概念详细阅读
一、不定积分的概念原函数定义：设f（x）是定义某区间I上的已知函数，若存在一个函数F（x），对于该区间上每一点都满足：F′（x）=f（x）或dF（x）=f（x）dx，则称F（x）是f（x）在该区间I上的一个原函数.如已知f（x）=2x，由于F（x）=x2满足F′（x）=（x2）′=2x，所以F（x）=x2是f（x）=2x的一个原函数.同理，x2+1，x2-1，x2+10等也都是f（x）=2x的原函......
2023-11-20
-
高等数学：曲面积分的概念与性质详细阅读
在本章第一节的质量问题中，如果把曲线改为曲面，并相应地把线密度ρ（x，y）改为面密度ρ（x，y，z），小段曲线的弧长Δsi改为小块曲面的面积ΔSi，而第i小段上面的一点（ξi，ηi）改为第i小块曲面上的一点（ξi，ηi，ζi），那么在面密度为ρ（x，y，z）连续的前提下，所求的质量M就是下列和的极限：其中λ表示n小块曲面的直径的最大值.抽去它们的具体意义，就得出对面积的曲面积分的概念.定义1 设曲......
2023-10-19
-
合同法：承诺的概念、性质和要件详细阅读
承诺一经生效，合同即告成立。(三) 要件依我国法律规定，一项有效的承诺，必须具备以下构成要件:1.承诺必须由受要约人作出。要约是向特定人作出的，其只对特定人生效，即只有该特定人才有权针对要约进行承诺，承诺必须由受要约人作出。相对人对承诺的实质内容作出扩张、限制或者变更的，不能构成承诺，而形成反要约。承诺一旦超过承诺期限作出，便不再为承诺，而是向要约人发出的一个新要约。......
2023-08-12
-
定积分的几何意义-高等数学 上册详细阅读
若函数f（x）≥0，则在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形的面积.当函数f（x）≤0时，由定积分定义知在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形（在x轴下方）的面积的相反数.图5－3一般地，若f（x）在［a，b］上既取得正值又取得负值，则在几何上表示在x轴上方图形的面积减去x轴下方图形的面积所得之差.如图5－3所示，有由几何意义易知，在......
2023-11-19
相关推荐