性质1设函数f(x)的原函数存在,k为非零常数,则证因为,所以类似可证明不定积分有下列性质.性质2设函数f(x)与g(x)的原函数均存在,则性质2可推广到有限个函数的情形.利用不定积分的性质和基本积分公式可以求一些简单函数的不定积分.对于不定积分运算需要指出,虽然每个积分号都含有任意常数,但任意常数之和仍是任意常数,所以遇到几个任意常数时只要写一个任意常数即可.例5求解例6求解积分运......
2023-11-19
一、原函数与不定积分
定义4.1 设f(x)是定义在区间I上的函数,如果存在函数F(x),对于任意x∈I,都有
F′(x)=f(x)或dF(x)=f(x)dx
则称函数F(x)为函数f(x)在区间I上的一个原函数.
例如,因为(sinx)′=cosx,则sinx是cosx的原函数.
又因为(sinx+1)′=cosx,所以sinx+1也是cosx的原函数.
由此例可以看出,一个函数若有原函数,则原函数可以不止一个.
实际上,若函数F(x)为函数f(x)的一个原函数,即F′(x)=f(x),则(F(x)+C)′=f(x)(其中,C为任意常数),所以F(x)+C都是f(x)的原函数.
所以,函数f(x)的原函数有无穷多个.
另一方面,如果F(x),G(x)为函数f(x)在区间I上的任意两个原函数,即[F(x)]′=f(x),[G(x)]′=f(x),则[G(x)-F(x)]′=G′(x)-F′(x)=f(x)-f(x)=0所以G(x)-F(x)=C,即G(x)=F(x)+C.
所以,函数f(x)的任意两个原函数仅相差一个常数.
定义4.2 函数f(x)的所有原函数称为f(x)的不定积分,记作∫f(x)dx.其中,∫称为积分号,f(x)称为被积函数,f(x)dx称为被积表达式,x称为积分变量.
因此,若F(x)是f(x)的一个原函数,那么∫f(x)dx=F(x)+C.
例1 求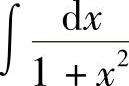 .
.
解 由于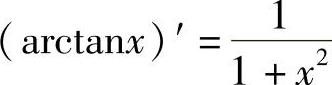 ,所以arctanx是
,所以arctanx是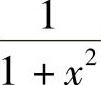 的一个原函数,因此
的一个原函数,因此
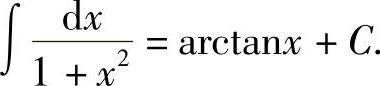
例2 求函数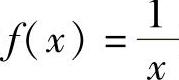 的不定积分.
的不定积分.
解 当x>0时,由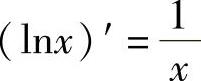 ,得
,得
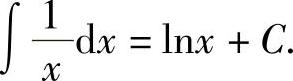
当x<0时,由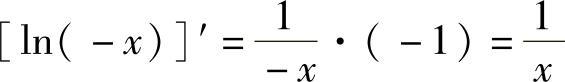 ,得
,得

综合两种情况,可得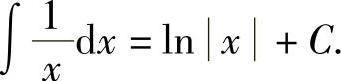
二、不定积分的性质
[∫f(x)dx]′=f(x)或d[∫f(x)dx]=f(x)dx;∫F′(x)dx=F(x)+C或∫dF(x)=F(x)+C.
由导数运算的线性性质,还可以得到如下性质:
1)∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx;2)∫kf(x)dx=k∫f(x)dx(k为常数,k≠0).
证 1)[∫f(x)dx+∫g(x)dx]′=[∫f(x)dx]′+[∫g(x)dx]′=f(x)+g(x).
推广之,有限个函数的和也有这一性质.(www.chuimin.cn)
2)类似可证.
此外,至于函数f(x)在什么条件下才有原函数,将在下一章给出说明,先给出结论:
若函数f(x)在某一区间上连续,则在此区间上f(x)的原函数一定存在.
三、基本积分公式
因为求不定积分是求导数的逆运算,则由基本导数公式对应地可以得到基本积分公式:
1)∫kdx=kx+C(k是常数);2)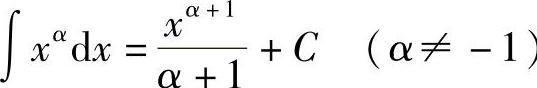 );3)
);3)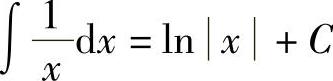 ;4)
;4)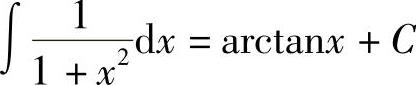 ;5)
;5)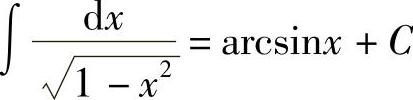 ;6)∫exdx=ex+C;7)
;6)∫exdx=ex+C;7)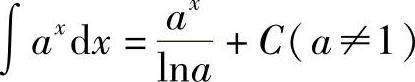 ;8)∫cosxdx=sinx+C;9)∫sinxdx=-cosx+C;10)∫sec2xdx=tanx+C;11)∫csc2xdx=-cotx+C;12)∫secxtanxdx=secx+C;13)∫cscxcotxdx=-cscx+C.
;8)∫cosxdx=sinx+C;9)∫sinxdx=-cosx+C;10)∫sec2xdx=tanx+C;11)∫csc2xdx=-cotx+C;12)∫secxtanxdx=secx+C;13)∫cscxcotxdx=-cscx+C.
例3 求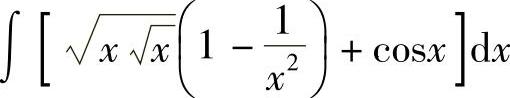 .
.
解 
例4 求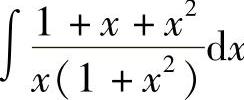 .
.
解 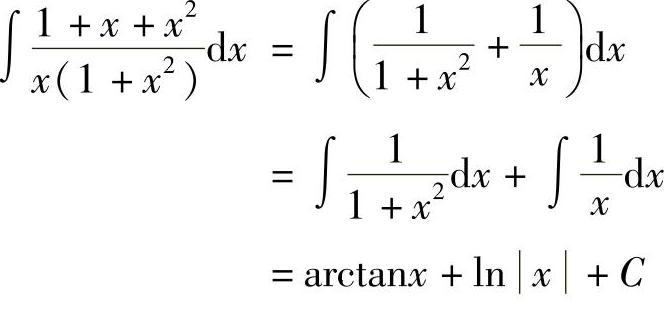
例5 求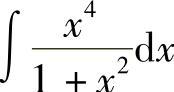 .
.
解 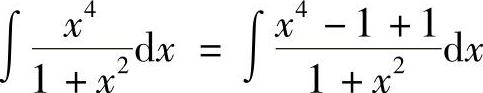
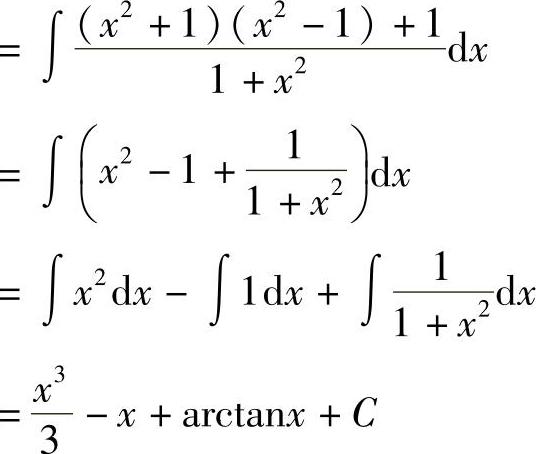
例6 求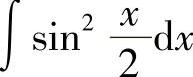 .
.
解 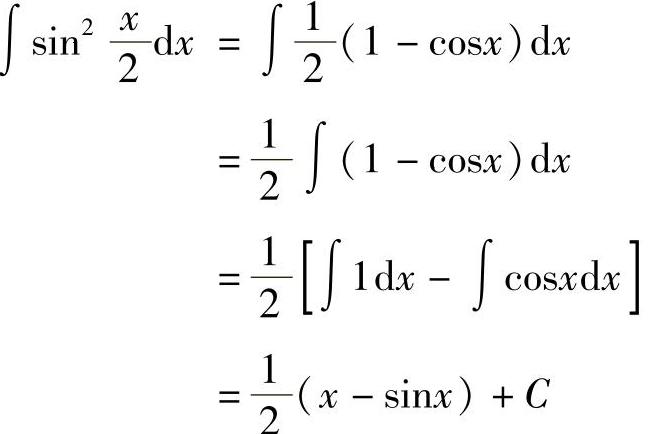
四、不定积分的几何意义
由于函数f(x)的不定积分F(x)+C中含有任意常数,因此在几何上,对于每一个确定的常数值C,都相应地有一条曲线,称为f(x)的积分曲线.显然这样的曲线有无数条,它们可以由曲线y=F(x)沿y轴方向上下移动而得到,称为f(x)的积分曲线族(见图4-1).
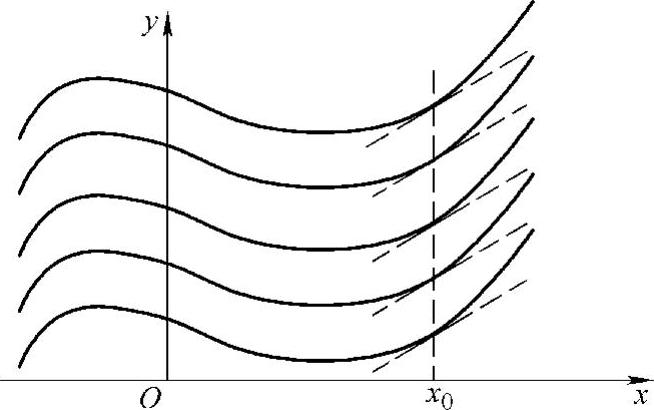
图4-1
积分曲线族中的每一条曲线,对应于同一横坐标x=x0处有相同的斜率f(x0),则在x=x0处它们的切线互相平行(见图4-1).
例7 已知曲线在点P(x,y)的切线斜率 ,且曲线经过点
,且曲线经过点 ,求此曲线方程.
,求此曲线方程.
解 设曲线方程为y=f(x),由假设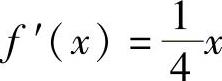 ,有
,有
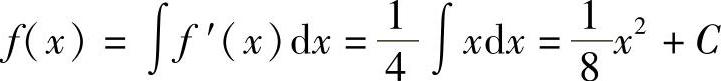
即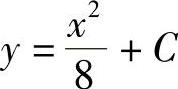 ,C为常数.
,C为常数.
由于曲线经过点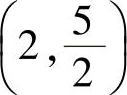 ,以此点坐标代入方程,得
,以此点坐标代入方程,得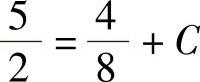 ,解得C=2.
,解得C=2.
因此所求方程为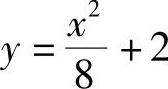 (见图4-2).
(见图4-2).
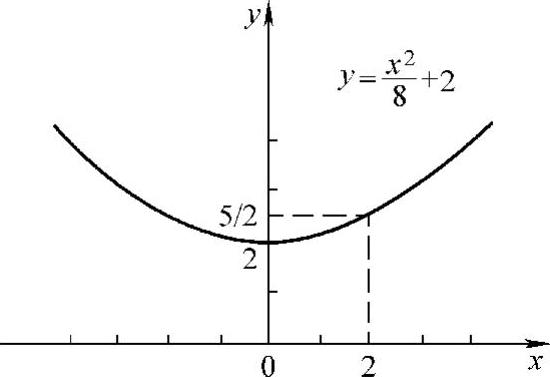
图4-2
有关高等数学(上、下册)的文章

性质1设函数f(x)的原函数存在,k为非零常数,则证因为,所以类似可证明不定积分有下列性质.性质2设函数f(x)与g(x)的原函数均存在,则性质2可推广到有限个函数的情形.利用不定积分的性质和基本积分公式可以求一些简单函数的不定积分.对于不定积分运算需要指出,虽然每个积分号都含有任意常数,但任意常数之和仍是任意常数,所以遇到几个任意常数时只要写一个任意常数即可.例5求解例6求解积分运......
2023-11-19

一、不定积分的概念原函数定义:设f(x)是定义某区间I上的已知函数,若存在一个函数F(x),对于该区间上每一点都满足:F′(x)=f(x)或dF(x)=f(x)dx,则称F(x)是f(x)在该区间I上的一个原函数.如已知f(x)=2x,由于F(x)=x2满足F′(x)=(x2)′=2x,所以F(x)=x2是f(x)=2x的一个原函数.同理,x2+1,x2-1,x2+10等也都是f(x)=2x的原函......
2023-11-20

在本章第一节的质量问题中,如果把曲线改为曲面,并相应地把线密度ρ(x,y)改为面密度ρ(x,y,z),小段曲线的弧长Δsi改为小块曲面的面积ΔSi,而第i小段上面的一点(ξi,ηi)改为第i小块曲面上的一点(ξi,ηi,ζi),那么在面密度为ρ(x,y,z)连续的前提下,所求的质量M就是下列和的极限:其中λ表示n小块曲面的直径的最大值.抽去它们的具体意义,就得出对面积的曲面积分的概念.定义1 设曲......
2023-10-19

一、引例1.曲边梯形的面积设函数y=f(x)在闭区间[a,b]上非负且连续,则曲线y=f(x)与直线x=a,x=b,y=0围成的图形(见图5-1)称为曲边梯形.求其面积A的基本思想是在很小的区间上用小矩形面积近似代替小梯形面积.图5-1第一步:分割.用一串分点a=x0<x1<…......
2023-11-22

定义2若F(x)是f(x)在区间I上的一个原函数,则称F(x)+C为f(x)在区间I上的不定积分,记作即∫f(x)dx=F(x)+C其中C为任意常数,记号“∫”称为积分号,f(x)称为被积函数,f(x)dx称为被积表达式,x称为积分变量.由定义2可知,求的关键就是求出f(x)的一个原函数,不定积分与原函数是总体与个体的关系.由此,本节开头所举的两个例子可写作从不定积分的定义即可知下述关系:或又由......
2023-11-19

利用函数极限的定义,可得下列极限的性质.1)唯一性定理2若存在,则极限唯一.证(反证法)假设极限不唯一,则存在两个不相等的常数a,b,使得均成立.不妨设b>a,由于取则δ1>0,当x满足0<|x-x0|<δ1时,恒有即又由于仍取则δ2>0,当x满足0<|x-x0|<δ2时,恒有即取δ=min{δ1,δ2},则当x满足0<|x-x0|<δ时,上面(1-5)、(1-6)两式均成立,但这是不可能的.......
2023-11-19

一、函数的有界性如果对属于某一区间I的所有x值总有│f(x)│≤M成立,其中M是一个与x无关的常数,那么我们就称f(x)在区间I有界,否则便称无界.注:一个函数,如果在其整个定义域内有界,则称为有界函数.例如:函数y=cosx在(-∞,+∞)内是有界的.再如:当x∈(-∞,+∞)时,恒有|sinx|≤1,所以函数f(x)=sinx在(-∞,+∞)内是有界函数.这里M=1(当然,也可以取大于1的任何......
2023-11-20
相关推荐