椭圆曲率半径与磨损问题

2023-11-22 理论教育版权反馈

【摘要】：解设椭圆.由例2可知，椭圆在点处的曲率最大，即曲率半径最小，且为图3-22显然砂轮半径不超过时才不会产生过量磨损或有的地方磨不到的问题.对于砂轮磨削一般工件的内表面时，也有类似的结论，即选用砂轮的半径不应超过这工件内表面的截线上各点处曲率半径中的最小值.

一、弧微分

作为曲率的预备知识，先介绍弧微分的概念.

设函数f（x）在区间（a，b）内具有连续导数，其图形为（见图3-16），并规定依x增大的方向作为曲线y=f（x）的正向.对曲线上任一点M（x，y），规定有向弧段的值为s（简称为弧s）显然，弧s与x存在函数关系：s=s（x）.而且s（x）是x的单调增加函数.下面求s（x）的导数及微分.

设x，x+Δx为（a，b）内两个邻近的点，它们在曲线y=f（x）上的对应点为M，M′（见图3-16），并设对应于x的增量Δx，弧s的增量为Δs，于是

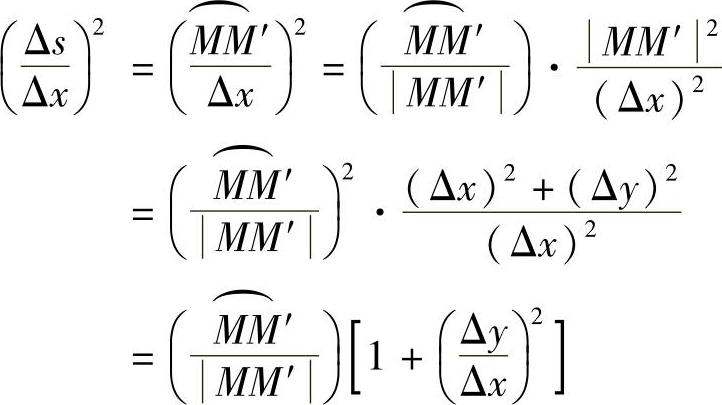
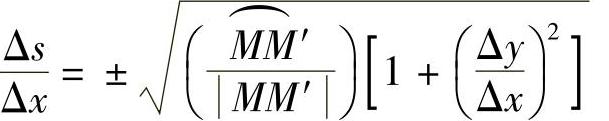
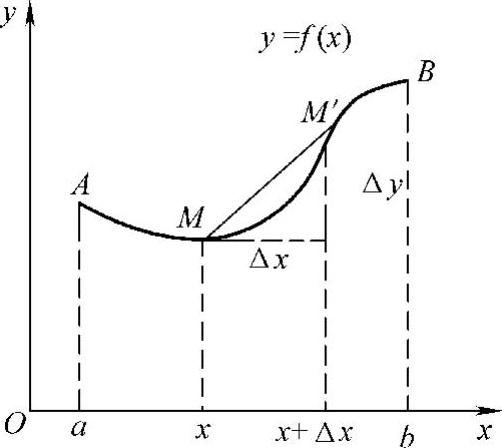
图3-16

令Δx→0取极限，由于Δx→0时，M→M′，这时弧的长度与弦的长度之比的极限为1，又因为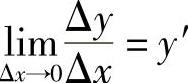，因此得

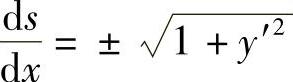
由于s=s（x）是单调增加函数，从而根号前应取正数，于是有

这就是弧微分公式.

二、曲率及其计算公式

在工程技术中，有时需要研究曲线的弯曲程度，如船体结构中的钢梁，机床的转轴等.可以观察到，直线不弯曲，半径较小的圆弯曲程度得比半径较大的圆大些，而其他曲线的不同部分有不同的弯曲程度，比如，抛物线y=x²在顶点附近弯曲的比远离顶点的部分厉害些.下面研究如何用数量来描述曲线的弯曲程度.

如图3-17所示，弧段比较平直，当动点沿这弧段从M移动到M′时切线转过的角度不大；而弧段弯曲得厉害，动点沿这弧段从M′移动到M″时切线转过的角度就比较大.

但是，切线转过的角度的大小还不能完全反映曲线弯曲的程度.如图3-18所示，尽管两弧段的切线转过的角度相同，然而弯曲程度却不相同，短弧段比长弧段弯曲得厉害些.由此可见，曲线弧的弯曲程度还与弧段的长度有关.

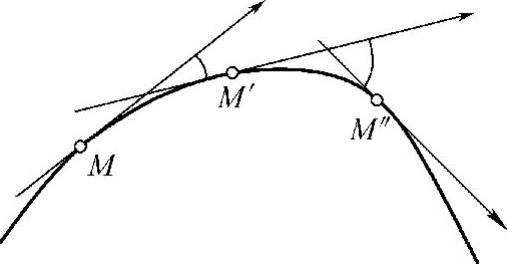
图3-17

图3-18

按照上面分析，引入描述曲线弯曲程度的曲率概念如下.

在光滑弧上自点M开始取弧段，其长为Δs.对应切线转角为Δα，如图3-19所示.

用单位弧段上切线转过的角度的大小来表示弧段的弯曲程度，把这比值叫做弧段的平均曲率，并记作K，即

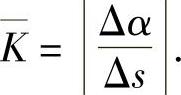
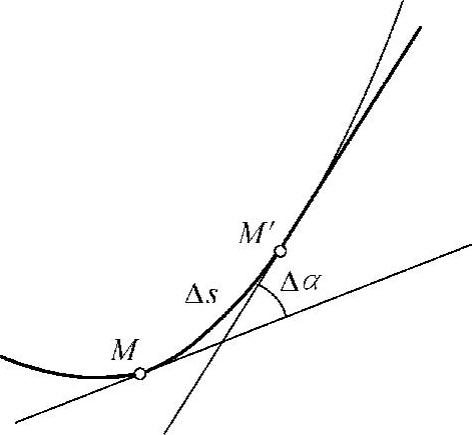
图3-19

类似于从平均速度引进瞬时速度的方法，当Δs→0时（即M′→M时），上述平均曲率的极限叫做曲线y=f（x）在点M处的曲率，记作K，即

在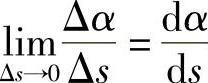存在的条件下，K也可以表示为

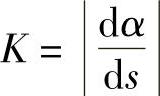
对于直线而言，切线与直线本身重合，当点在直线上移动时，切线的转角不变，所以Δα=0，从而K=0.也就是说直线上任一点的曲率都为零，这与人们直觉认识到的“直线不弯曲”一致.

设圆的半径为R，如图3-20所示，Δs=RΔα，所以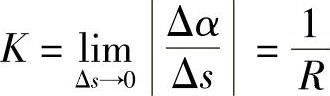.这说明圆上任一点处曲率都等于半径的倒数，也就是说，圆的弯曲程度是一样的，且半径越小曲率越大，即圆弯曲得越厉害.

在一般情况下，可由式子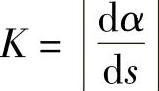导出便于实际计算曲率的公式.

设曲线的直角坐标方程是y=f（x），且f（x）具有二阶导数.(www.chuimin.cn)

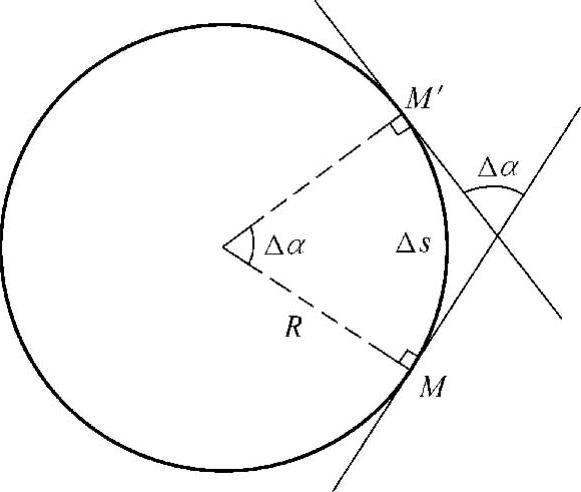
图3-20

因为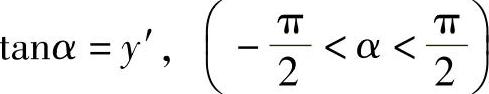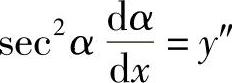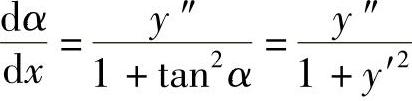，，于是由弧微分公式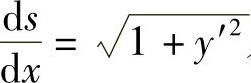及曲率的公式，得

设曲线由参数方程

给出，则可利用由参数方程所确定的函数的求导方法，得到曲率的计算公式

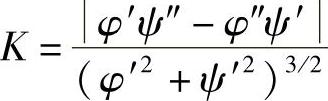
例1 抛物线y=ax²+bx+c上哪一点处的曲率最大？

解将y′=2ax+b，y″=2a，代入公式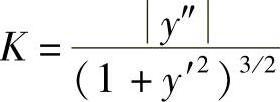，得

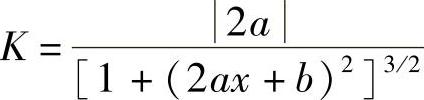
因为分子是常数|2a|，所以要使曲率K最大，只要使分母最小即可.容易看出，当2ax+b=0时，即时分母最小，从而曲率K最大.因此，抛物线在顶点处的曲率最大.

在有些实际问题中，如果|y′|同1比起来很小的话，则|y′|可以忽略不计，从而可得曲率的近似计算公式

K≈|y″|

例2 讨论椭圆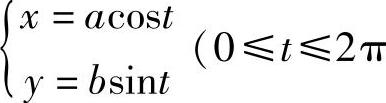，0＜b＜a）在何处曲率最大？

解 x′=-asint，x″=-acost，y′=bcost，y″=-bsint

令f（t）=a²sin²t+b²cos²t，因为分子是常数ab，所以当且仅当分母f（t）取最小值时K最大.

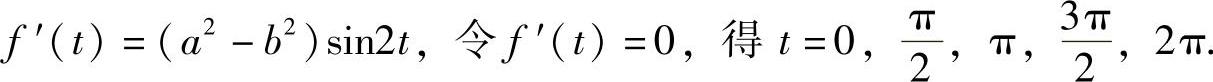
计算驻点处的函数值并进行比较得知，在t=0，π，2π时f（t）取最小值，从而K取最大值，说明椭圆在点（±a，0）处的曲率最大.

三、曲率圆与曲率半径

设曲线y=f（x）在点M（x，y）处的曲率为K（K≠0）.在点M处的曲线的法线上，在凹的一侧取一点D，使|DM|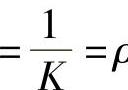.以D为圆心，ρ为半径作圆（见图3-21），这个圆叫作曲线在点M处的曲率圆，曲率圆的圆心D叫作曲线在点M处的曲率中心，曲率圆的半径ρ叫作曲线在点M处的曲率半径.

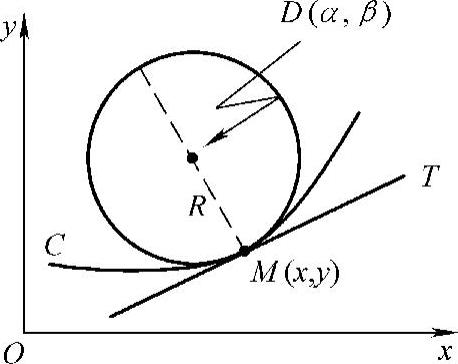
图3-21

按照上述规定，曲率圆与曲线在点M处有相同的切线和曲率，且在点M邻近有相同的凹向.因此，在实际问题中，常用曲率圆在点M邻近的一段圆弧来近似代替曲线弧，以使问题简化.

由上面规定，曲线在点M处的曲率K（K≠0）与曲线在点处的曲率半径ρ有如下关系：

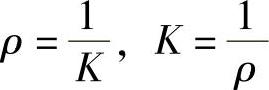
例3 设一工件内表面的截痕是一椭圆（见图3-22），现要用砂轮磨削其内表面，问选择半径多大的砂轮比较合适？

解设椭圆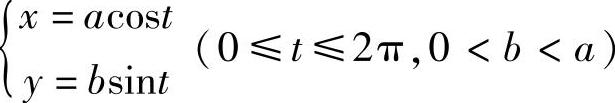.由例2可知，椭圆在点（±a，0）处的曲率最大，即曲率半径最小，且为

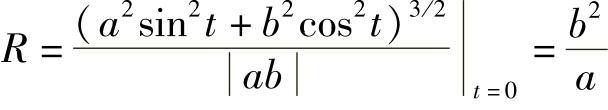
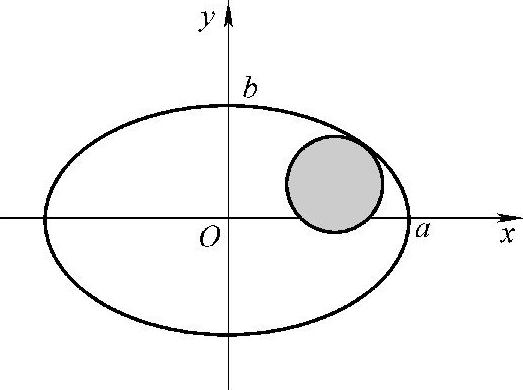
图3-22

显然砂轮半径不超过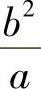时才不会产生过量磨损或有的地方磨不到的问题.

对于砂轮磨削一般工件的内表面时，也有类似的结论，即选用砂轮的半径不应超过这工件内表面的截线上各点处曲率半径中的最小值.

椭圆曲率半径与磨损问题

相关推荐