【摘要】:解 设AD=x,那么DB=100-x,由于铁路上每千米货运的运费与公路上每公里货运的运费之比为3∶5,因此不妨设铁路上每公里的运费为3k,公路上每公里的运费为5k.图3-10设从B点到C点需要的总运费为y,那么y=5k·CD+3k·DB,即得目标函数.现在来求x在区间[0,100]上取何值时,函数y的值最小.求导数:.令y′=0,得x=15.由于,,其中,以yx=15=380k为最小,因此当AD=15km时,总运费最省.
一、函数的极值
定义3.3 设函数y=f(x)在点x0的某去心邻域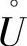 (x0)内有定义,并且对于任意
(x0)内有定义,并且对于任意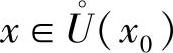 ,有
,有
f(x0)>f(x)(或f(x0)<f(x)),则称f(x0)为函数f(x)的极大值(或极小值),x0称为函数f(x)的极大值点(或极小值点).
极大值与极小值统称为极值,极大值点与极小值点统称为极值点.
如图3-8所示,函数f(x)在点x2、x5处取得极大值,在点x1、x4、x6处取得极小值.
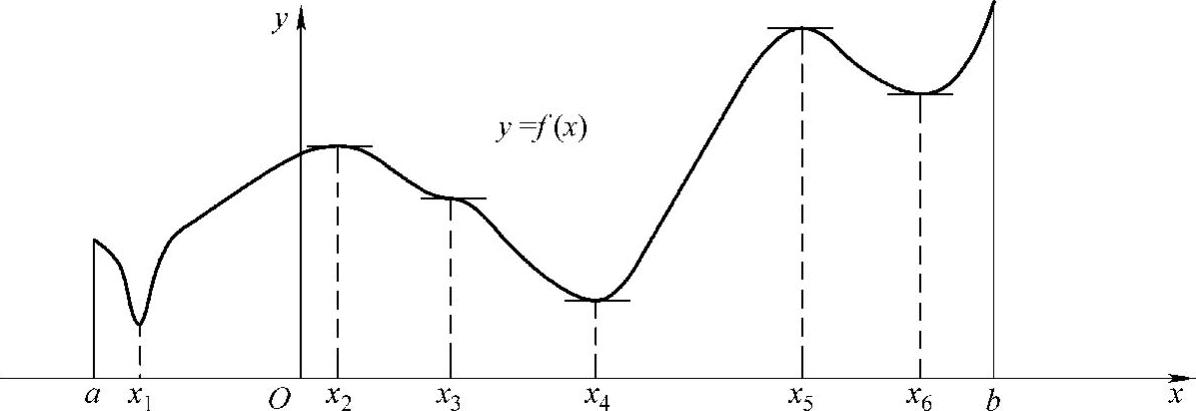
图3-8
从图3-8中还可以看出,在可导的极值点处,如x2、x4、x5和x6,曲线的切线是水平的.
定理3.9 (极值的必要条件)若y=f(x)在点x0处可导,且x0是函数y=f(x)的极值点,则f′(x0)=0.
证 不妨设x0是函数y=f(x)的极大值点,即存在x0的某去心邻域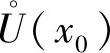 ,对于任意
,对于任意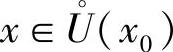 ,有f(x)<f(x0),因此,当x>x0时,
,有f(x)<f(x0),因此,当x>x0时,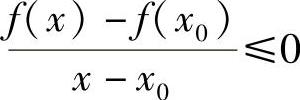 ;当x<x0时,
;当x<x0时,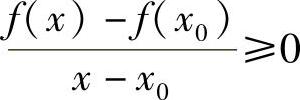 .
.
由f(x)在点x0可导及极限的保号性,有
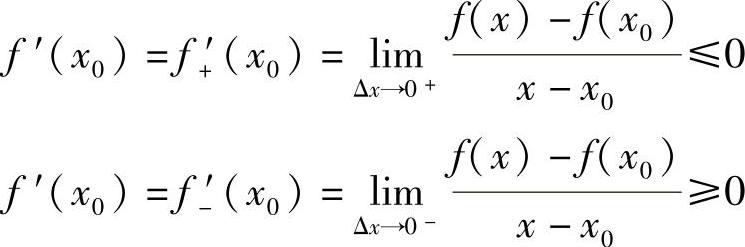
于是有f′(x0)=0.
极小值类似可证,在此不再赘述.
定义3.4 使导数为零的点称为函数f(x)的驻点.
可导函数f(x)的极值点必定是它的驻点;反之,驻点却不一定是极值点,如图3-8所示,曲线中的x3.
从图3-8中可以看出,如x1、x2、x4、x5和x6,极值点的两侧适当小邻域内,函数单调性相反,由此可得到判定极值的充分条件.
定理3.10 (极值的第一充分条件)设函数f(x)在点x0处连续,且在x0的某去心邻域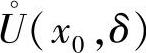 内可导,
内可导,
1)当x∈(x0-δ,x0)时,f′(x)>0,而当x∈(x0,x0+δ)时,f′(x)<0,函数f(x)在点x0处取得极大值;
2)当x∈(x0-δ,x0)时,f′(x)<0,而当x∈(x0,x0+δ)时,f′(x)>0,函数f(x)在点x0处取得极小值;
3)当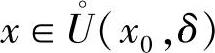 时,f′(x)的符号保持不变,则x0不是f(x)的极值点.
时,f′(x)的符号保持不变,则x0不是f(x)的极值点.
此定理的证明留与读者自证.
例1 求函数f(x)=2x3-3x2-12x+1的极值.
解 f′(x)=6x2-6x-12=6(x+1)(x-2),
令f′(x)=0,解得x1=-1,x2=2,
列表讨论如下:

所以,-1是函数f(x)的极大值点,极大值是f(-1)=8;2是函数f(x)的极小值点,极小值是f(2)=-19.
例2 讨论函数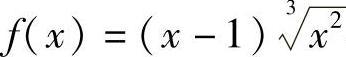 单调性和极值.
单调性和极值.
解 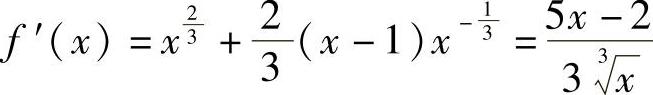 ,
,
当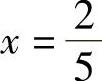 时,f′(x)=0;当x=0时,f′(x)不存在.
时,f′(x)=0;当x=0时,f′(x)不存在.
列表讨论如下:

所以,函数在x=0有极大值0,在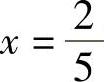 有极小值
有极小值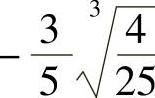 .
.
定理3.11 (极值的第二充分条件)设函数f(x)在x0处具有二阶导数且f′(x0)=0,f″(x0)≠0,则
1)当f″(x0)>0时,函数f(x)在x0处取得极小值;2)当f″(x0)<0时,函数f(x)在x0处取得极大值.
证 1)因为f′(x0)=0,利用导数定义有
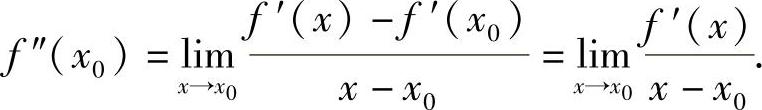
由f″(x0)>0及极限的保号性可知,在x0的某一去心邻域内有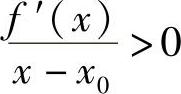 ,
,
当x<x0时,有f′(x)<0;当x>x0时,有f′(x)>0,由定理3.9可知,x0是函数f(x)的极小值点,f(x0)是极小值.
2)同理可证.(www.chuimin.cn)
例3 讨论函数f(x)=(x2-1)3+1的极值.
解 f′(x)=6x(x2-1)2,f″(x)=6(x2-1)(5x2-1),
令f′(x)=0,得驻点x1=-1,x2=0和x3=1,
f″(0)=6>0,故f(0)=0为极小值,
由于f″(-1)=f″(1)=0无法使用定理3.11判断,故需用极值的第一充分条件来判断.由于f′(x)在x=1的左、右邻域内同号,故f(x)在x=1处没有极值,同理f(x)在x=-1处也没有极值.
二、函数的最值
若函数f(x)在闭区间[a,b]上连续,则一定取得最大值和最小值.如果说极值是一个局部概念的话,那么最值就是个整体概念.
一般地,求连续函数f(x)在闭区间[a,b]上的最值,首先求出函数的全部驻点和不可导点,计算这些点的函数值再和区间端点函数值f(a)、f(b)进行比较,其中最大者就是区间[a,b]上的最大值,最小者就是区间[a,b]上的最小值.
例4 求f(x)=x3-3x2-9x+1在区间[-4,4]上的最大值和最小值.
解 由方程f′(x)=3x2-6x-9=0解得x=-1,x=3.
f″(x)=6x-6,f″(-1)=-12<0,f″(3)=12>0.
f(x)在x=-1取得极大值f(-1)=6;
f(x)在x=3取得极小值f(3)=-26;
端点处f(-4)=-75,f(4)=-19.
所以在[-4,4]上,函数最大值为6,最小值为-75.
例5 求函数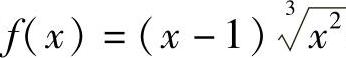 在[-1,1]上的最大值和最小值.
在[-1,1]上的最大值和最小值.
解 由例2知,函数f(x)在(-1,1)内有两个临界点,当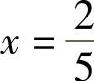 时,f′(x)=0;当x=0时,f′(x)不存在.
时,f′(x)=0;当x=0时,f′(x)不存在.
又因为f(0)=0,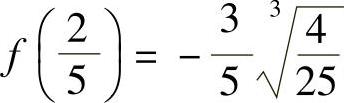 ,f(-1)=-2,f(1)=0,所以在[-1,1]上,函数最大值为0,最小值为-2.
,f(-1)=-2,f(1)=0,所以在[-1,1]上,函数最大值为0,最小值为-2.
对于求函数最值的应用题,有时可根据实际意义来判断可疑点是否为最值.
例6 一张高1.4m的图画挂在墙上,它的底边高于观察者的眼睛1.8m,则观察者站在距墙多远处看图最清楚(视角θ最大)?
解 如图3-9所示,设观察者距墙xm,则
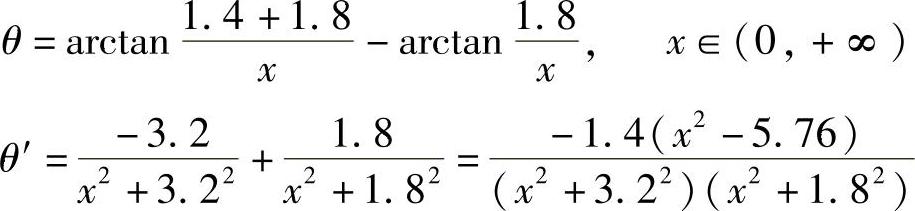
令θ′=0,得x=2.4.
根据问题的实际意义,观察者最佳站位一定存在,而驻点唯一,因此观察者站在距墙2.4m处时看图最清楚.
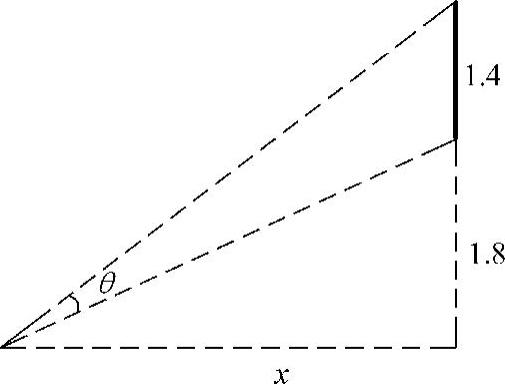
图3-9
例7 如图3-10所示,铁路线上AB段的距离为100km.工厂C距A处为20km,AC垂直于AB.为了运输需要,要在AB线上选定一点D向工厂修筑一条公路.已知铁路上每千米货运的运费与公路上每千米货运的运费之比为3∶5,为了使货物从供应站B运到工厂C的运费最省,问D点应选在何处?
解 设AD=x,那么DB=100-x,

由于铁路上每千米货运的运费与公路上每公里货运的运费之比为3∶5,因此不妨设铁路上每公里的运费为3k,公路上每公里的运费为5k(k为常数).
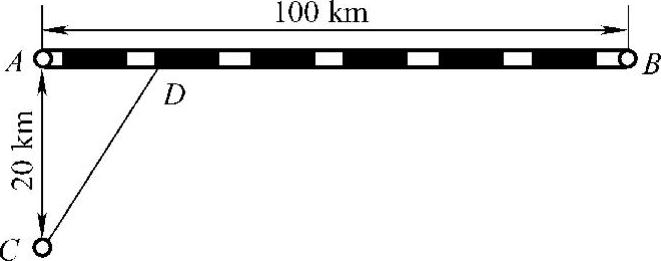
图3-10
设从B点到C点需要的总运费为y,那么
y=5k·CD+3k·DB,
即得目标函数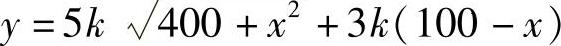 (0≤x≤100).
(0≤x≤100).
现在来求x在区间[0,100]上取何值时,函数y的值最小.
求导数: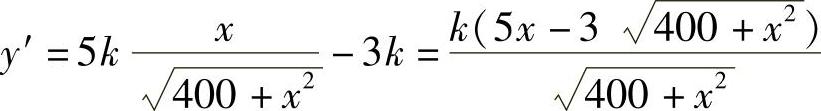 .
.
令y′=0,得x=15.
由于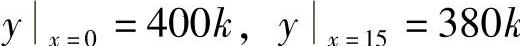 ,
,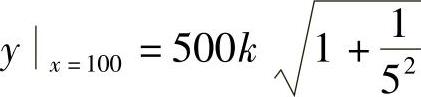 ,其中,以yx=15=380k为最小,因此当AD=15km时,总运费最省.
,其中,以yx=15=380k为最小,因此当AD=15km时,总运费最省.

 (
(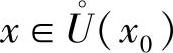 ,有
,有
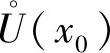 ,对于任意
,对于任意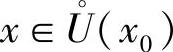 ,有
,有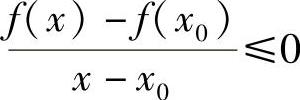 ;当
;当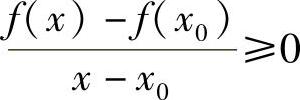 .
.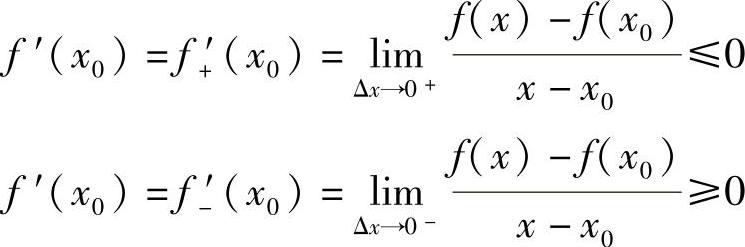
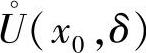 内可导,
内可导,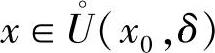 时,
时,
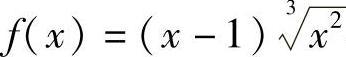 单调性和极值.
单调性和极值.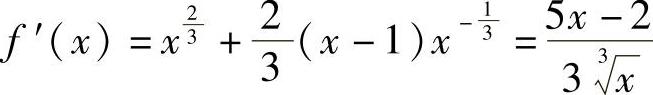 ,
,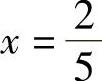 时,
时,
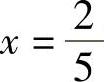 有极小值
有极小值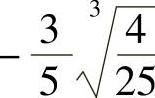 .
.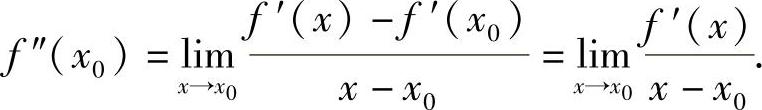
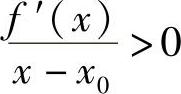 ,
,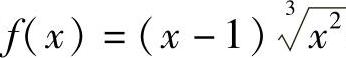 在[-1,1]上的最大值和最小值.
在[-1,1]上的最大值和最小值.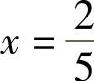 时,
时,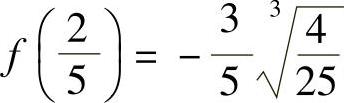 ,
,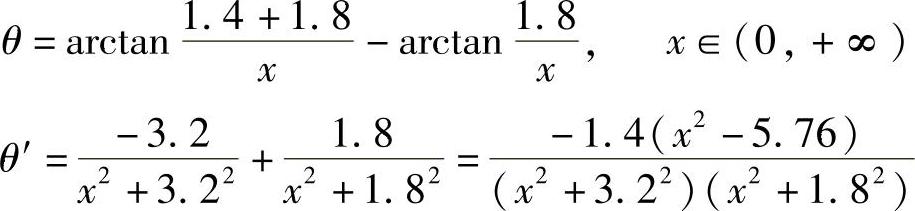



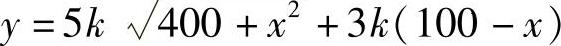 (0≤
(0≤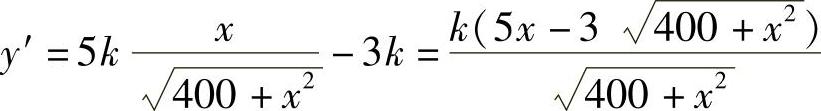 .
.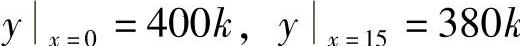 ,
,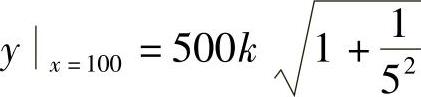 ,其中,以
,其中,以





相关推荐