首页理论教育高等数学：函数单调性和凹凸性

高等数学：函数单调性和凹凸性

2023-11-22 理论教育版权反馈

【摘要】：一、函数的单调性从图上可以直观地看出，单调增加函数的切线斜率非负（见图3-3），单调减少函数的切线斜率非正（见图3-4）.图3-3图3-4定理3.7 设函数f（x）在区间I内可导，则：1）对任意x∈I，有f′（x）＞0，则函数f（x）在I严格单调增加；2）对任意x∈I，有f′（x）＜0，则函数f（x）在I严格单调减少.证先证1）对任意x1，x2∈I且x1＜x2，函数f（x）在区间[x1，x2]上

一、函数的单调性

从图上可以直观地看出，单调增加函数的切线斜率非负（见图3-3），单调减少函数的切线斜率非正（见图3-4）.

图3-3

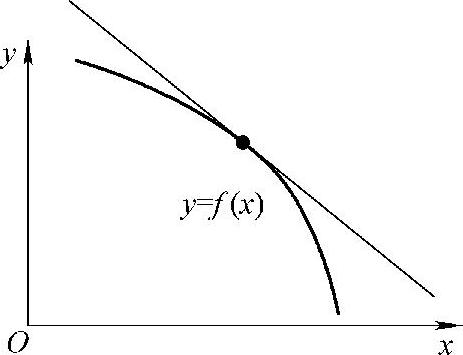
图3-4

定理3.7 设函数f（x）在区间I内可导，则：

1）对任意x∈I，有f′（x）＞0，则函数f（x）在I严格单调增加；

2）对任意x∈I，有f′（x）＜0，则函数f（x）在I严格单调减少.

证先证1）对任意x₁，x₂∈I且x₁＜x₂，函数f（x）在区间[x₁，x₂]上满足拉格朗日中值定理的条件，有

f（x₂）-f（x₁）=f′（ξ）（x₂-x₁）ξ∈（x₁，x₂），

已知f′（ξ）＞0，x₂-x₁>0，有f（x₂）-f（x₁）＞0.

即函数f（x）在I严格单调增加.

2）同理可证.

例1 讨论f（x）=3x-x³的单调性.

解 f′（x）=3-3x²=3（1-x）（1+x）.

令f′（x）=0，解得x=-1与x=1，它们将（-∞，+∞）分成（-∞，-1）、（-1，1）和（1，+∞）三个区间.

当x＜-1时，f′（x）＜0，f（x）在（-∞，-1）上严格单调减少；当-1＜x＜1时，f′（x）＞0，f（x）在（-1，1）上严格单调增加；当x＞1时，f′（x）＜0，f（x）在（1，+∞）上严格单调减少.

例2 求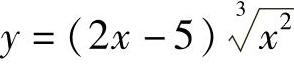的单调区间.

解在（-∞，+∞）上连续，当x≠0时，

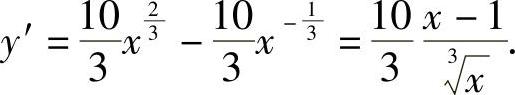
令y′=0，解得x=1；又因为当x=0时，函数的导数不存在；以x=0和x=1为分点将（-∞，+∞）分为（-∞，0）、（0，1）和（1，+∞）三个区间.

在（-∞，0）上，f′（x）＞0，所以f（x）在（-∞，0）上严格单调增加；

在（0，1）上，f′（x）＜0，所以f（x）在（0，1）上严格单调减少；

在（1，+∞）上，f′（x）＞0，所以f（x）在（1，+∞）上严格单调增加.

例3 证明：当x＞0时，x＞ln（1+x）.

证设f（x）=x-ln（1+x），则函数f（x）在[0，+∞）可导，

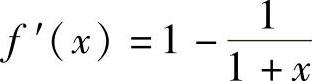
当x＞0时，f′（x）＞0，所以函数f（x）在（0，+∞）上严格单调增加.因此，当x＞0时，有f（x）＞f（0）=0，即x＞ln（1+x）.

二、函数的凹凸性

在研究函数的图形时，只研究函数的单调性还不能准确地反映图形的主要特性.如图3-5和图3-6所示，A、B两点之间的弧都是单调上升的，但它们的弯曲方向却有着明显的差别，这种差别就是直观上的“凹”与“凸”.

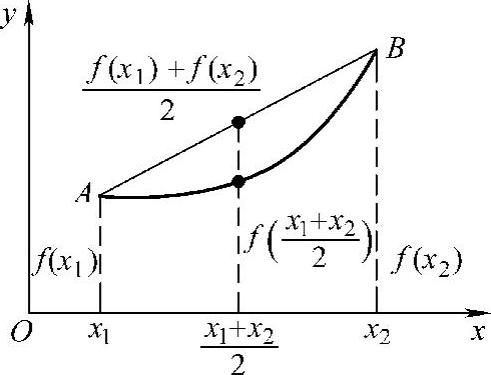
图3-5

图3-6

据此，在数学上作如下定义：

定义3.1 设f（x）在[a，b]上连续，如果对（a，b）内任意两点x₁和x₂，恒有(www.chuimin.cn)

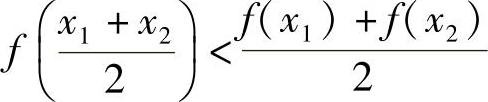
那么称f（x）在[a，b]上的图形是凹的；如果对（a，b）内任意两点x₁和x₂，恒有

那么称f（x）在[a，b]上的图形是凸的.

从几何图形上，可以观察切线斜率的变化来区分凹、凸两种弧.如图3-7所示.

图3-7

左侧的凹弧，切线斜率随着自变量的增加而增大，即f′（x）是单调增加的，也即f″（x）＞0；右侧的凸弧，切线斜率随着自变量的增加而减小，即f′（x）是单调减少的，也即f″（x）＜0.因此，对于凹凸的判定，可以通过判断二阶导数的符号来实现.

定理3.8 设f（x）在[a，b]上连续，在（a，b）内具有一阶和二阶导数，则：

1）若x∈（a，b）时，f″（x）＞0，则f（x）在[a，b]上的图形是凹的；2）若x∈（a，b）时，f″（x）＜0，则f（x）在[a，b]上的图形是凸的.

证 1）设x₁和x₂为[a，b]内任意两点，且x₁＜x₂，记，并记x₂^-x0=x₀-x₁=h，则x₁=x₀-h，x₂=x₀+h，由拉格朗日中值定理，得

f（x₀+h）-f（x₀）=f′（x₀+θ₁h）h （0＜θ₁＜1），

f（x₀）-f（x₀-h）=f′（x₀-θ₂h）h （0＜θ₂＜1），

两式相减，得

f（x₀+h）+f（x₀-h）-2f（x₀）=[f′（x₀+θ₁h）-f′（x₀-θ₂h）]h

对f′（x）在区间[x₀-θ₂h，x₀+θ₁h]上再用一次拉格朗日中值定理，得

[f′（x₀+θ₁h）-f′（x₀-θ₂h）]h=f″（ξ）（θ₁+θ₂）h²（x₀-θ₂h＜ξ＜x₀+θ₁h）

由1）的条件，f″（ξ）＞0，故有

即

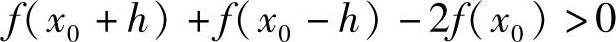
，亦即.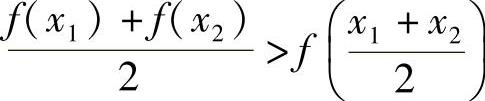

所以f（x）在[a，b]上的图形是凹的.

2）同理可证.

例4 讨论函数f（x）=arctanx的凹凸性.

解因为；

令f″（x）=0，解得x=0.

当x＜0时，f″（x）＞0，所以f（x）=arctanx在（-∞，0）内的图形是凹的；当x＞0时，f″（x）＜0，所以f（x）=arctanx在（0，+∞）内的图形是凸的.

定义3.2 曲线的凹凸的分界点称为曲线的拐点.

由定义可知，拐点为凹凸的分界点，则在拐点两侧适当小的范围内，f″（x）必然异号，所以在拐点处f″（x）=0或f″（x）不存在.

例5 求f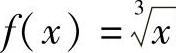的凹凸区间及对应曲线的拐点.

解该函数在（-∞，+∞）内连续，当x≠0时，，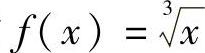

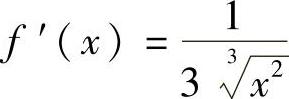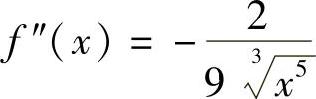
二阶导数在（-∞，+∞）内无零点，在x=0处f″（x）不存在，它把（-∞，+∞）分成两个部分区间.在（-∞，0）内，f″（x）＞0，曲线是凹的；在（0，+∞）内，f″（x）＜0，曲线是凸的，所以点（0，0）是曲线的拐点.

例6 求y=x⁴的凹凸区间及对应曲线的拐点.

解 y′=4x³，y″=12x²，当x=0时，y″=0；当x≠0时，y″＞0.

所以y=x⁴在（-∞，+∞）内函数图形是凹的，没有拐点.