【主要内容】1.型未定式极限的洛必达法则设,则称型未定式极限,这里的x0可以换成x0-,x0+,∞,-∞及+∞.型未定式极限的洛必达法则(以x→x0情形为例)是:设函数f(x),g(x)在点x0的某个去心邻域内可导,且g′(x)≠0.如果,且存在或为无穷大,则注 (ⅰ)对型未定式极限在使用洛必达法则之前应尽量进行化简,如利用极限运算法则算出其中非未定式部分的极限,对f(x)或g(x)作等价无穷小代......
2023-10-27
在求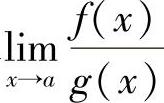 或
或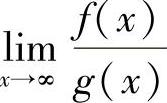 时,若发现f(x)和g(x)同时趋于0,或同时趋于∞,如
时,若发现f(x)和g(x)同时趋于0,或同时趋于∞,如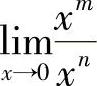 ,
,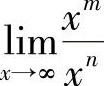 ,则上述极限可能存在,也可能不存在.要根据具体的函数来进一步确定,通常把这种极限称为
,则上述极限可能存在,也可能不存在.要根据具体的函数来进一步确定,通常把这种极限称为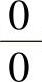 或
或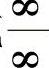 型的未定式,这种未定式是不能用商的极限运算法则来计算的.在这一节中,可以利用洛必达法则来解决这类问题.
型的未定式,这种未定式是不能用商的极限运算法则来计算的.在这一节中,可以利用洛必达法则来解决这类问题.
一、“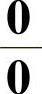 ”型未定式
”型未定式
定理3.4 (洛必达法则)设函数f(x)和g(x)满足条件:
1) ;2)在点a的某个去心邻域U°(a)内都可导,且g′(x)≠0;3)
;2)在点a的某个去心邻域U°(a)内都可导,且g′(x)≠0;3)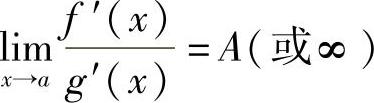 ;则
;则 ).
).
证 在点x=a处补充定义f(x)=g(x)=0,则函数f(x)与g(x)在点x=a点连续.
对任意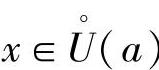 ,在以x和a为端点的区间上,由柯西中值定理,则在x与a之间存在一点ξ,使得
,在以x和a为端点的区间上,由柯西中值定理,则在x与a之间存在一点ξ,使得 .
.
又因为ξ在x与a之间,所以当x→a时,有ξ→a,上式两边取极限,得
将此定理中的x→a换成其他的自变量变化过程亦成立,证明从略.
例1 求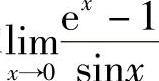 .
.
解 由洛必达法则,有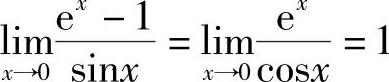 .
.
例2 求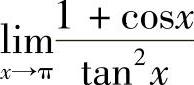 .
.
解 由洛必达法则,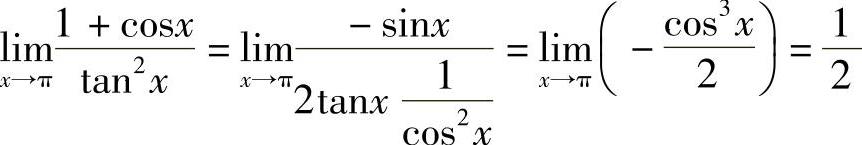 .
.
求一个未定式的极限时,如果一阶导数之比还是未定式,只要仍满足洛必达法则的条件,则可以再次使用洛必达法则.倘若结果还是未定式,那么还可以继续使用洛必达法则.
例3 求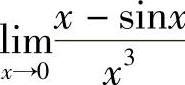 .
.
解 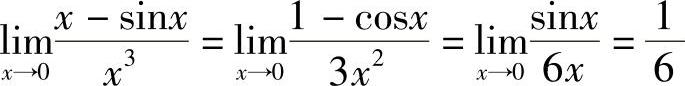 .二、“
.二、“ ”型未定式
”型未定式
定理3.5 设函数f(x)与g(x)满足:
1)在点a的某个去心邻域U°(a)内都可导,且g′(x)≠0;2)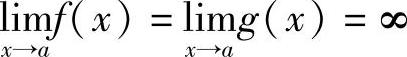 ;3)
;3)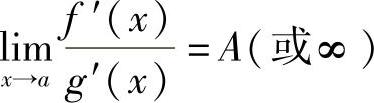 ;则
;则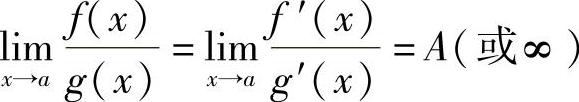 .将此定理中的x→a换成其他的自变量变化过程亦成立,证明从略.
.将此定理中的x→a换成其他的自变量变化过程亦成立,证明从略.
例4 求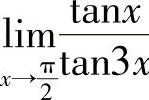 .
.
解 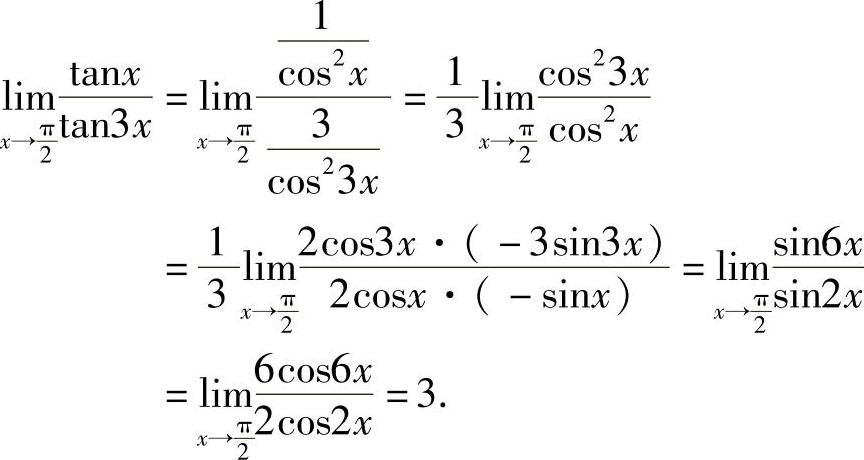
例5 求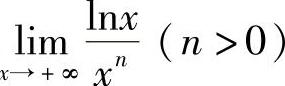 .(www.chuimin.cn)
.(www.chuimin.cn)
解 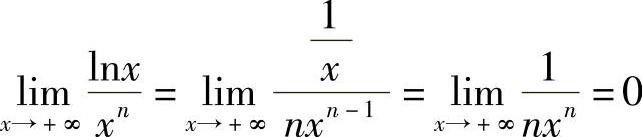 .
.
例6 求极限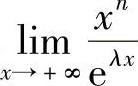 (n为正整数,λ>0).
(n为正整数,λ>0).
解 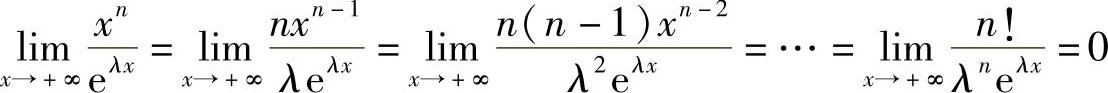 .三、其他型未定式
.三、其他型未定式
例7 求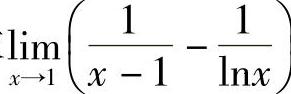 .
.
解 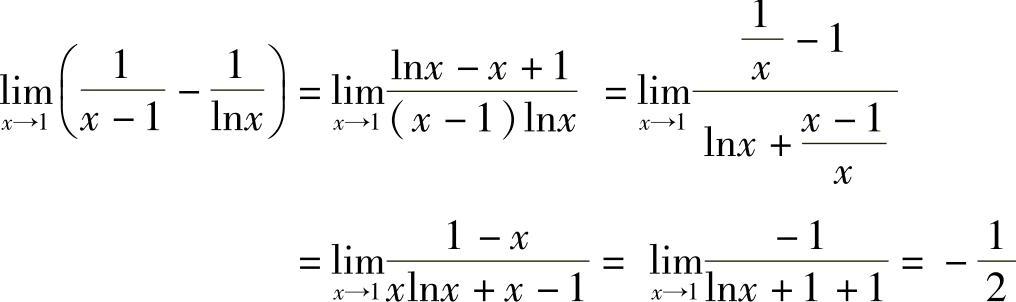 .
.
例8 求极限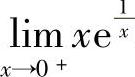 .
.
解 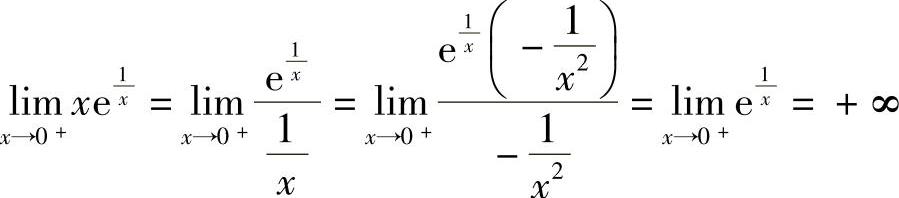 .
.
例9 求 .
.
解 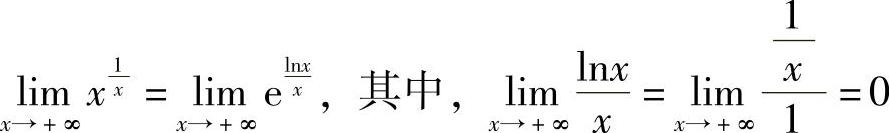 ,则
,则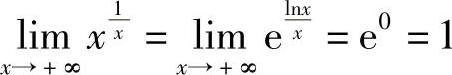 .
.
例10 求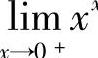 .
.
解 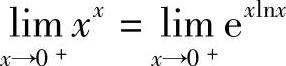 ,其中,
,其中,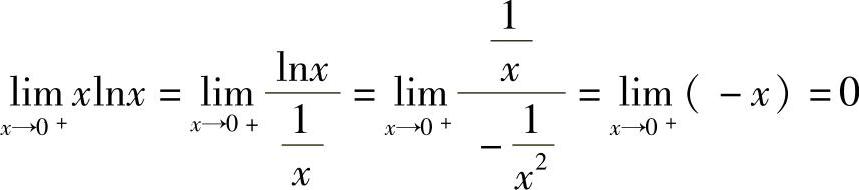 ,则
,则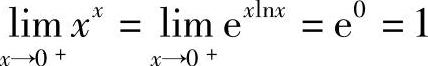 .
.
例11 求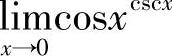 .
.
解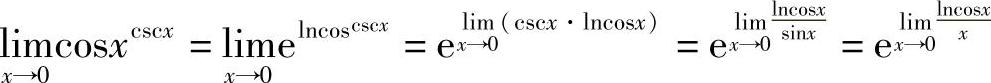
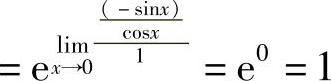 .
.
例12 求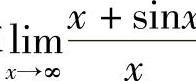 .
.
解 极限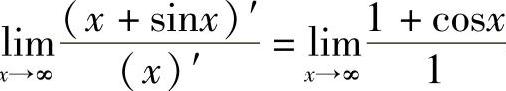 不存在,不能应用洛必达法则.实际上,
不存在,不能应用洛必达法则.实际上,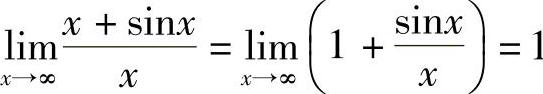 .
.
例13 求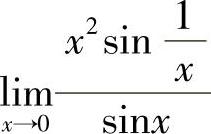 .
.
解 这是“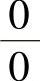 ”型未定式,因极限
”型未定式,因极限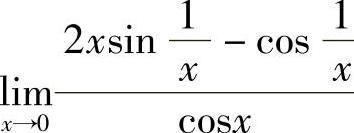 不存在,所以有
不存在,所以有
例14 求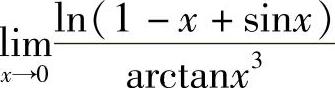 .
.
解 先用等价无穷小代换,再用洛必达法则.
有关高等数学(上、下册)的文章

【主要内容】1.型未定式极限的洛必达法则设,则称型未定式极限,这里的x0可以换成x0-,x0+,∞,-∞及+∞.型未定式极限的洛必达法则(以x→x0情形为例)是:设函数f(x),g(x)在点x0的某个去心邻域内可导,且g′(x)≠0.如果,且存在或为无穷大,则注 (ⅰ)对型未定式极限在使用洛必达法则之前应尽量进行化简,如利用极限运算法则算出其中非未定式部分的极限,对f(x)或g(x)作等价无穷小代......
2023-10-27

先给出两个无穷小之比的极限的洛必达法则.定理1(洛必达法则)如果函数f(x),g(x)满足:①②在x0的某个去心邻域内,f′(x),g′(x)都存在,且g′(x)≠0;③存在(或为无穷大),则证因为极限与函数f(x),g(x)在x=x0处的值无关,所以不妨重新定义f(x0)=g(x0)=0,则在x=x0处重新定义后的函数f(x),g(x)在x0处连续,设x是x0的去心邻域内的任一点,再由条件①......
2023-11-19

南宋理宗端平元年,宋蒙联合攻破金朝最后的“都城”蔡州,金哀宗完颜守绪自杀身亡,金朝灭亡。后来的杨谊部尚未到达洛阳,在城东遭蒙古军的伏击,几乎全军覆没。蒙古军队趁机掩击,宋军大部被消灭。“端平入洛”对南宋政局产生了深远影响,使蒙古有了进攻南宋的口实,同时由于入洛宋军损失严重,削弱了宋军的战斗力。入洛失败加剧了南宋政权的内部纷争,导致人心涣散。......
2023-08-29

图4.35旋转头这种方法将机器上料的前后操作时间减少到最低限度,因为旋转可以在没有任何移动或操作装置很少移动的情况下运行。图4.42集成电路的旋转模块这些模块通过附加轴进行扩展,允许简单旋转的附加运动自由度。图4.43适用于不同应用的电动旋转变位模块机械手或工具旋转有关的一个主要问题是上料。......
2023-06-15

冰淇淋哲学是台湾台塑企业董事长王永庆在对自己的经营事业进行总结后得出的一个结论。在将台塑产量扩大6倍的同时,王永庆又创办了一个加工台塑产品的公司,即南亚塑胶工业公司,专为台塑进行下游加工生产。其含义就在于冬天卖冰淇淋,生意清淡,必定促使卖者努力改善经营管理。......
2023-12-01

与抗日战争前以及抗日战争时相比,抗日战争胜利后上海信托业整体规模有所收缩,主要体现在机构数量递减、资本总额大幅缩水等方面。另外活期信托存款占信托存款总额比重过高,历年均占有90%以上。因此,该局吸收的信托存款并不能作为长期资金进行运用。1947年度中央信托局总收益中,投资证券和生产事业所得仅占总收益的1%。综上所述,不以信托业务为主业的问题,在抗日战争胜利后的上海信托业中仍然存在。......
2023-08-09

140.洛克忠告规定应该少定,一旦定下来之后,便要严格遵守。这被大家称为洛克忠告。孙武答应了,并挑选了一百个宫女,让吴王的两个宠姬担任队长,有板有眼地操练了起来。孙武再次讲解了要领,并要两个队长以身作则。孙武派人请吴王来检阅,吴王正为失去两个宠姬而惋惜,再没有心思来看宫女训练,只是派人告诉孙武:“先生的带兵之道我已领教,由你指挥的军队一定纪律严明,能打胜仗。”......
2023-12-01

1943年,美国心理学家马斯洛发表了《人类动机的理论》一书。马斯洛理论告诉我们,生理需求只是人们的最基本需求。商人以赚钱花钱为乐,企业家以创造更大价值为乐,商人一直待在马斯洛需求的最底层,沉迷于生理需求;而企业家待在马斯洛需求的金字塔顶尖,实现人世间自我价值的最大化。......
2023-12-01
相关推荐