首页理论教育高等数学（上、下册）：罗尔定理及应用

高等数学（上、下册）：罗尔定理及应用

2023-11-22 理论教育版权反馈

【摘要】：一、罗尔定理定理3.1 若函数f（x）满足条件：1）在[a，b]上连续；2）在（a，b）内可导；3）在区间端点处的函数值相等，即f（a）=f（b）；则在（a，b）内至少存在一点ξ，使得f′（ξ）=0.证如图3-1所示，因为f（x）在[a，b]上连续，由连续函数的性质，f（x）在[a，b]上必有最大值M和最小值m.1）如果m=M，则f（x）在[a，b]上恒为常数M，因此在（a，b）内恒有f（x）=

一、罗尔定理

定理3.1 若函数f（x）满足条件：

1）在[a，b]上连续；

2）在（a，b）内可导；

3）在区间端点处的函数值相等，即f（a）=f（b）；

则在（a，b）内至少存在一点ξ，使得f′（ξ）=0.

证如图3-1所示，因为f（x）在[a，b]上连续，由连续函数的性质，f（x）在[a，b]上必有最大值M和最小值m.

1）如果m=M，则f（x）在[a，b]上恒为常数M，因此在（a，b）内恒有f（x）=M，于是，在整个区间（a，b）内恒有f′（x）=0，（a，b）内每一点都可取为ξ，定理成立.

2）如果m＜M，因为f（a）=f（b），则M与m中至少有一个不等于端点a处的函数值f（a），设M≠f（a）（如果设m≠f（a），证法完全类似），从而，在（a，b）内至少有一点ξ，使得f（ξ）=M.下面证明f′（ξ）=0.

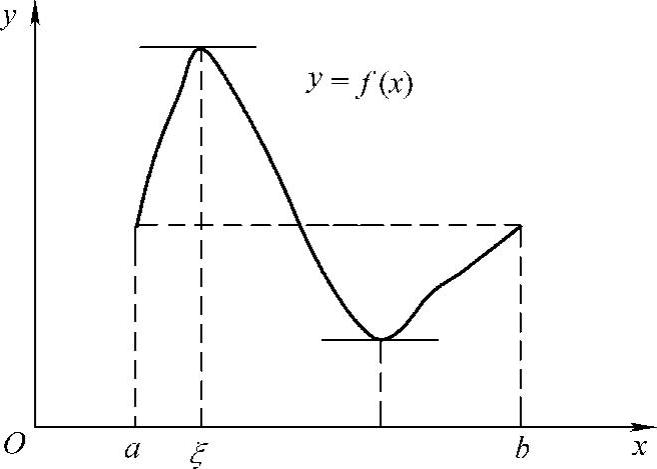
图3-1

事实上，因为f（ξ）=M是最大值，所以不论Δx为正或负，只要ξ+Δx∈（a，b），恒有f（ξ+Δx）≤f（ξ），由f（x）在ξ点可导的条件及极限的保号性

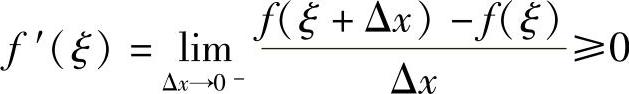
因此必有f′（ξ）=0.

定理的几何意义为，设有一段连续曲线，它的两端点的高度相等，且除两端点外，曲线上处处都有不垂直于x轴的切线，则曲线上至少有一点处的切线平行于x轴.

例1 不求出函数f（x）=（x-1）（x-2）（x-3）（x-4）的导数，说明方程f′（x）=0有几个实根，并指出它们所在的区间.

解因为f（x）=（x-1）（x-2）（x-3）（x-4）在[1，4]上可导，且

f（1）=f（2）=f（3）=f（4），所以f（x）在[1，2]，[2，3]，[3，4]上满足罗尔定理的条件.因此f′（x）=0至少有三个实根，分别位于区间（1，2）、（2，3）、（3，4）内.

又因为f′（x）是三次多项式，故f′（x）=0至多有三个实根，于是方程f′（x）=0恰有三个实根，分别位于区间（1，2），（2，3），（3，4）内.

二、拉格朗日定理

定理3.2 若函数f（x）满足条件：

1）在[a，b]上连续；

2）在（a，b）内可导.则至少存在一点ξ∈（a，b）使得

f（b）-f（a）=f′（ξ）（b-a）

即.

如图3-2所示，定理的几何意义是：是割线AB的斜率，而f′（ξ）是曲线y=f（x）在点C（ξ，f（ξ））处的切线的斜率.拉格朗日定理的意义是：若区间[a，b]上有一条连续曲线，曲线上每一点都有切线，则曲线上至少有一点C（ξ，f（ξ）），过C点的切线与割线平行.

证由几何意义可知，罗尔定理是拉格朗日定理的特殊情况，

为此，构造一个辅助函数F（x）=（b-a）f（x）-[f（b）-f（a）]x.可知F（x）在[a，b]上连续，且在（a，b）内可导.

图3-2

又因为F（b）=bf（a）-af（b）=F（a），从而F（x）满足罗尔定理的条件，则在（a，b）内至少存在一点ξ，使得F′（ξ）=0.

即f（b）-f（a）=f′（ξ）（b-a）或.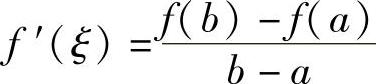

由a＜ξ＜b，可得ξ=a+θ（b-a）（0＜θ＜1）

所以，拉格朗日中值定理又可写成：(www.chuimin.cn)

f（b）-f（a）=f′[a+θ（b-a）]·（b-a）（0＜θ＜1），

称之为拉格朗日中值定理的有限增量形式.

例2 证明.

证设f（x）=ln（1+x），则f（x）在[0，x]上满足拉格朗日中值定理的条件，且

f（x）-f（0）=f′（ξ）（x-0），（0＜ξ＜x）

即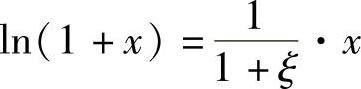，又因为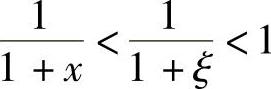，且x＞0，从而得

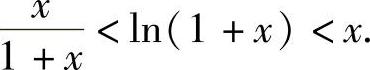
推论3.1 若函数f（x）在区间（a，b）内的导数恒为零，则函数f（x）在区间（a，b）内恒为常数.

证在区间（a，b）内任意取两点x₁和x₂，设x₁＜x₂，则f（x）在区间[x₁，x₂]上满足拉格朗日中值定理的条件，则有

f（x₂）-f（x₁）=f′（ξ）（x₂-x₁）ξ∈（x₁，x₂）

由已知，f′（ξ）=0，可得f（x₁）=f（x₂），

因此，区间（a，b）内任意两点的函数值相等，即函数f（x）在区间（a，b）内恒为常数.

推论3.2 若函数f（x）和g（x）在区间（a，b）内的导数都相等，则函数f（x）和g（x）在区间（a，b）内至多相差一个常数.

证设F（x）=f（x）-g（x），由推论3.1可知在区间（a，b）内，

F（x）=C，即f（x）=g（x）+C.

例3 证明：.

证对于任意给定的x∈（-1，1），有.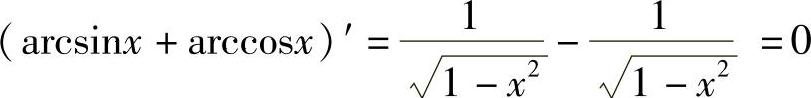

从而由推论3.1可知，

arcsinx+arccosx=C （C为常数）.

又令x=0，得

，

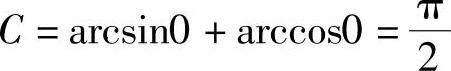即.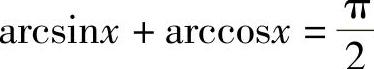

三、柯西中值定理

定理3.3 若函数f（x）与g（x）满足条件：

1）在闭区间[a，b]上连续；

2）在开区间（a，b）内可导；

3）对任意x∈（a，b），有g′（x）≠0；则至少存在一点ξ∈（a，b）使得

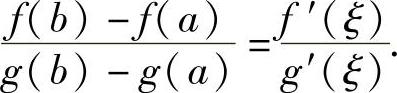
证首先，可以推出g（b）-g（a）≠0.否则，若g（b）=g（a），则由罗尔定理可知，在（a，b）内至少存在一点ξ，使得g′（ξ）=0，这与条件3）矛盾.

作辅助函数F（x）=[f（b）-f（a）]g（x）-[g（b）-g（a）]f（x），有F（x）在[a，b]上连续，且在（a，b）内可导，

F（a）=g（a）f（b）-g（b）f（a）=F（b）.

因此，F（x）满足罗尔定理的条件，则在（a，b）内至少存在一点ξ，使得F′（ξ）=0，即 [g（b）-g（a）]·f′（ξ）-[f（b）-f（a）]·g′（ξ）=0，从而有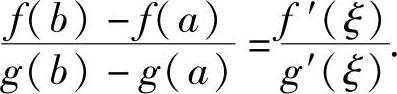

特别地，当g（x）=x时，柯西中值定理就变成拉格朗日中值定理.