一、罗尔定理定理3.1 若函数f(x)满足条件:1)在[a,b]上连续;2)在(a,b)内可导;3)在区间端点处的函数值相等,即f(a)=f(b);则在(a,b)内至少存在一点ξ,使得f′(ξ)=0.证 如图3-1所示,因为f(x)在[a,b]上连续,由连续函数的性质,f(x)在[a,b]上必有最大值M和最小值m.1)如果m=M,则f(x)在[a,b]上恒为常数M,因此在(a,b)内恒有f(x)=......
2023-11-22
一、微分的概念
1.引例
一块正方形金属薄片受温度变化的影响,边长由x0变到x0+Δx,此薄片面积改变了多少?
如图2-3所示,设薄片边长为x,面积为A,则A=x2,当x在x0取得增量Δx时,面积的增量ΔA=(x0+Δx)2-x02=2x0Δx+(Δx)2.
ΔA包括两部分,第一部分2x0Δx是Δx的线性函数,第二部分(Δx)2为Δx的高阶无穷小.因此,当Δx很小时,就可以用2x0Δx来近似代替ΔA.用微分dA来表示,记作dA=2x0Δx.

图2-3
2.微分
定义2.3 设函数y=f(x)在x0的某个邻域内有定义,若函数y=f(x)在x0的改变量Δy与自变量x的改变量Δx满足
Δy=AΔx+ο(Δx)其中,A是与Δx无关的常数,则称函数y=f(x)在点x0处可微,AΔx称为函数f(x)在点x0处的微分,表示为dy=AΔx或df(x0)=AΔx.
dy通常也称为Δy的线性主部.
二、可微与可导的关系
定理2.6 函数y=f(x)在x0可微的充分必要条件是函数y=f(x)在x0可导,且A=f′(x0).即
dy=f′(x0)Δx.
证 先证必要性.
设函数f(x)在x0可微,即Δy=AΔx+ο(Δx),其中,A是与Δx无关的常数,两边同除以Δx,得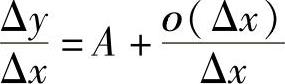 ,有
,有 ,
,
所以函数y=f(x)在x0可导,且A=f′(x0).
再证充分性.
设函数y=f(x)在x0可导,即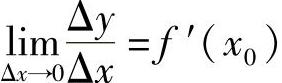
则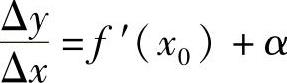 ,α→0(当Δx→0时).
,α→0(当Δx→0时).
从而Δy=f′(x0)Δx+αΔx=f′(x0)Δx+ο(Δx),其中,f′(x0)是与Δx无关的常数,ο(Δx)是比Δx高阶的无穷小,于是函数f(x)在x0可微,且A=f′(x0).
若对于函数y=x求微分,可得
dy=dx=(x)′·Δx=Δx.
于是函数f(x)在点x处的微分又可写作dy=f′(x)dx或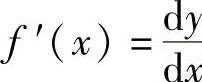 .在这个意义下,导数又叫做微商.
.在这个意义下,导数又叫做微商.
三、几何意义
如图2-4所示,PM是曲线y=f(x)在点P(x0,f(x0))处的切线.已知切线PM的斜率tanφ=f′(x0).
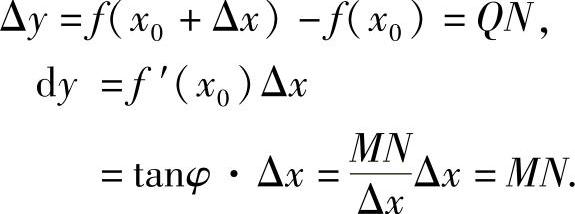
由此可见,dy=MN是曲线y=f(x)在点P(x0,y0)的切线PM的纵坐标的增量.因此,用dy近似代替Δy,就是用在点P(x0,y0)处切线的纵坐标的增量MN近似代替函数f(x)的增量QN,QM=QN-MN=Δy-dy=ο(Δx).(www.chuimin.cn)
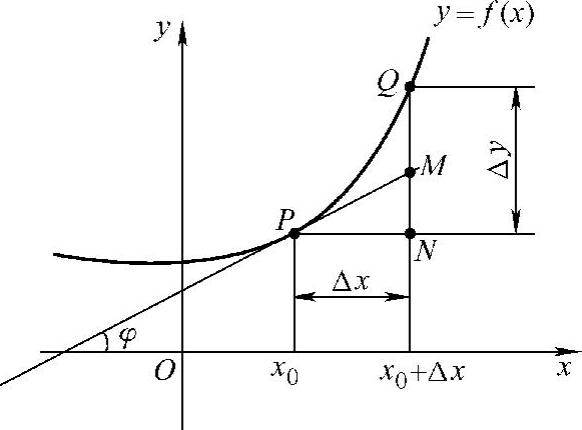
图2-4
四、微分法则
由dy=f′(x)dx,求微分dy,只要求出导数f′(x),再乘以dx即可.由导数公式和运算法则可相应地得到微分公式和微分运算法则:
1)dc=0 2)d(xμ)=μxμ-1dx;3)d(sinx)=cosxdx;4)d(cosx)=-sinxdx;5)d(tanx)=sec2xdx;6)d(cotx)=-csc2xdx;7)d(secx)=secx·tanxdx;8)d(cscx)=-cscx·cotxdx;9)d(ax)=axlnadx;10)d(ex)=exdx;11) ;12)
;12)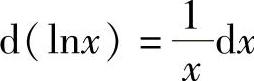 ;13)
;13)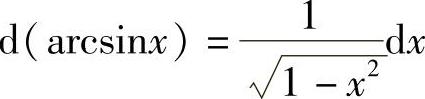 ;14)
;14)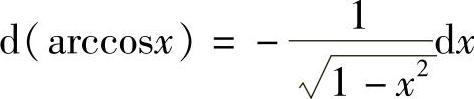 ;15)
;15) ;16)
;16)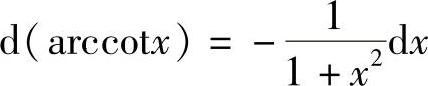 ;17)d(u±v)=du±dv;18)d(uv)=vdu+udv;19)
;17)d(u±v)=du±dv;18)d(uv)=vdu+udv;19)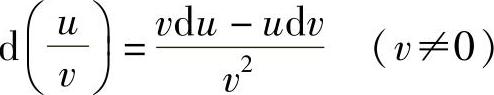 .
.
五、微分形式不变性
设y=f(u),u=φ(x),则复合函数y=f(φ(x))的微分为
dy=yx′dx=f′(u)φ′(x)dx.
由于φ′(x)dx=du,所以复合函数y=f(φ(x))的微分公式也可以写成
dy=f′(u)du或dy=yu′du.
由此可见,无论u是自变量还是自变量的可导函数,微分形式dy=f′(u)du保持不变,这一性质称为微分形式不变性.
例1 求y=exsinx的微分.
解 方法一:利用微分公式dy=f′(x)dx,得
dy=(exsinx)′dx=ex(sinx+cosx)dx.
方法二:利用微分形式不变性,得
dy=sinxdex+exdsinx=ex(sinx+cosx)dx.
六、微分在近似计算中的应用
若函数y=f(x)在x0可微,则Δy=dy+ο(Δx),即
f(x0+Δx)-f(x0)=f′(x0)Δx+ο(Δx).当|Δx|→0时,忽略高阶无穷小量,得
f(x)≈f(x0)+f′(x0)Δx.
例2 求tan31°的近似值.
解 设f(x)=tanx,
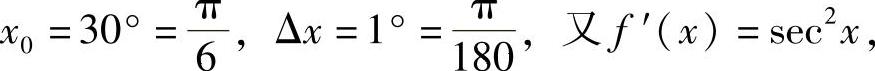
有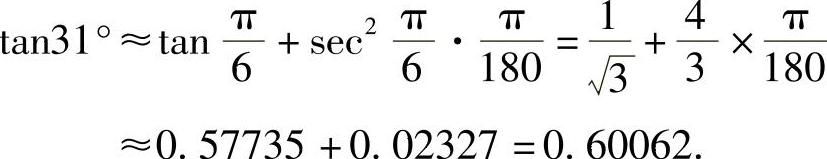
例3 求e-0.01的近似值.
解 设f(x)=ex,x0=0,Δx=-0.01,又f′(x)=ex,有e-0.01≈e0+e0(-0.01)=0.99.
有关高等数学(上、下册)的文章

一、罗尔定理定理3.1 若函数f(x)满足条件:1)在[a,b]上连续;2)在(a,b)内可导;3)在区间端点处的函数值相等,即f(a)=f(b);则在(a,b)内至少存在一点ξ,使得f′(ξ)=0.证 如图3-1所示,因为f(x)在[a,b]上连续,由连续函数的性质,f(x)在[a,b]上必有最大值M和最小值m.1)如果m=M,则f(x)在[a,b]上恒为常数M,因此在(a,b)内恒有f(x)=......
2023-11-22

一、第一类换元法在上一节中,虽已介绍了一些求原函数的方法,但这些方法在有些情况下是不够的.例如,∫cos2xdx就不易求解.如果令2x=u,可得代回原变量,得.一般地,设f(u)是u的连续函数,且∫f(u)du=F(u)+C,若u=φ(x)有连续的导数φ′(x),则∫f(φ(x))φ′(x)dx=F(φ(x))+C要证明上式成立,只需证明[F(φ(x))]′=f(φ(x))φ′(x)即可.因为[F......
2023-11-22

【主要内容】1.函数微分的定义设函数y=f(x)在点x0的某个邻域内有定义.如果y在点x0处的增量Δy=f(x0+Δx)-f(x0) (其中,Δx是自变量x在点x0处的增量)可表示为Δy=AΔx+o(Δx)(其中,A与Δx无关,o(Δx)表示Δx→0时比Δx高阶的无穷小),则称y=f(x)在点x0处可微,称Δy的线性主部AΔx为y=f(x)在点x0处的微分,记为dy|x=x0(注意:函数y=f(x......
2023-10-27

若u=u(x)与v=v(x)都有连续的导数,则由函数乘积的求导公式(uv)′=u′v+uv′,移项得uv′=(uv)′-u′v.对这个等式两边求不定积分,得∫uv′dx=uv-∫u′vdx,即∫udv=uv-∫vdu.这个公式称为分部积分公式.一般地,当∫udv不易计算而∫vdu较易计算时,就使用这个公式.例1 求∫xcosxdx.解 设u=x,则dv=cosxdx,du=dx,v=sinx,利用......
2023-11-22

一、差分与差分方程的一般概念定义6.3 设函数y=f,记为yx,则差yx+1-yx称为yx的一阶差分,简称为差分,记为Δyx,即Δyx=yx+1-yx.定义6.4 yx的一阶差分的差分Δ(Δyx)=Δ=-,记为Δ2yx,称为yx的二阶差分,即Δ2yx=Δ(Δyx)=yx+2-2yx+1+yx.同样定义三阶差分,四阶差分,…......
2023-11-22

一、渐近线首先介绍曲线的渐近线,它规范着无穷远处函数曲线的走向.定义3.5 若曲线上的一点沿着曲线趋于无穷远处时,该点到某直线的距离趋于零,则称此直线为曲线的渐近线.按直线的走向,渐近线可分为3种,即水平渐近线、铅直渐近线和斜渐近线.1)水平渐近线:平行于x轴的渐近线称为水平渐近线.设曲线y=f(x)的定义域是无限区间,若或(b为常数),则y=b就是曲线y=f(x)的一条水平渐近线.2)铅直渐近线......
2023-11-22

【知识点回顾】y=f(x)的微分定义:由函数的增量Δy=f(x0+Δx)-f(x0)=f′(x0)Δx+o(Δx)我们把增量的近似值称为函数f(x)在点x0处的微分,即我们已经学习了一元函数的微分的概念,现在我们用类似的思想方法来学习多元函数的全增量,从而把微分的概念推广到多元函数.这里以二元函数为例.全微分的定义:设二元函数z=f(x,y)在点(x0,y0)的一个邻域内有定义,则在点(x0,y0......
2023-11-20
相关推荐