解析函数不仅有一阶导数,而且有各高阶导数,它的值也可以用函数在边界上的值通过积分来表示.但是对于一元实函数来说,它在某一区间上可导,其导数在这区域上是否连续也不一定,更不要说它有高阶导数存在了.关于解析函数的高阶导数我们有下面的定理.定理2 解析函数f(z)的导数仍为解析函数,它的n阶导数为其中C为在函数f(z)的解析区域D内围绕z0 的任何一条正向简单闭曲线,而且它的内部全含于D.证明 设z0为......
2023-10-30
高等数学：高阶导数在线求解
【摘要】：一、高阶导数一般地，若函数y=f的导数y′=f′仍然可导，这个导数就称为原来函数y=f的二阶导数，记作y″，f″或.类似地，若y″=f″的导数存在，称为y=f的三阶导数，记作y，f或.一般地，如果y=f的（n-1）阶导数y（n-1）=f（n-1）的导数存在，其导数就称为y=f的n阶导数，记作y，f或.二阶和二阶以上的导数统称为高阶导数.例1 求n次多项式y=a0xn+a1xn-1+…
一、高阶导数
一般地，若函数y=f（x）的导数y′=f′（x）仍然可导，这个导数就称为原来函数y=f（x）的二阶导数，记作y″，f″（x）或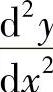
.
类似地，若y″=f″（x）的导数存在，称为y=f（x）的三阶导数，记作y‴，f‴（x）或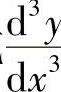
.
一般地，如果y=f（x）的（n-1）阶导数y（n-1）=f（n-1）（x）的导数存在，其导数就称为y=f（x）的n阶导数，记作y（n），f（n）（x）或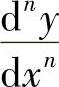
.
二阶和二阶以上的导数统称为高阶导数.
例1 求n次多项式y=a0xn+a1xn-1+…+an-1x+an的各阶导数.
解 y′=na0xn-1+（n-1）a1xn-2+…+an-1
y″=n（n-1）a0xn-2+（n-1）（n-2）a1xn-3+…+2an-2
继续求导下去，易知
y（n）=n！a0它是一个常数，则
y（n+1）=y（n+2）=…=0.
例2 求y=ex的各阶导数.
解 由（ex）′=ex，易知，对任何n，有（ex）（n）=ex.(www.chuimin.cn)
例3 求y=sinx的各阶导数.
解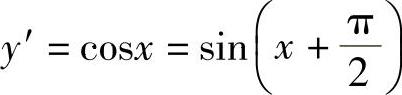 
，
同理可得，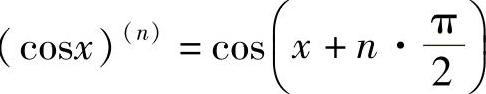
.
类似于一阶导数的运算法则，高阶导数有如下公式：
1）（u±v）（n）=u（n）±v（n）；2）（Cu）（n）=Cu（n）（C为常数）.
二、隐函数及参数方程所确定的函数的高阶导数
例4 由参数方程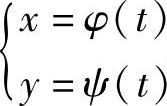
确定y为x的函数，若x=φ（t）与y=ψ（t）都是二阶可导的，且φ′（t）≠0，求y对x的二阶导数
.
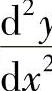解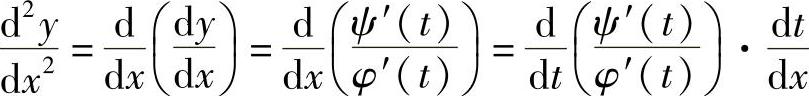 
.
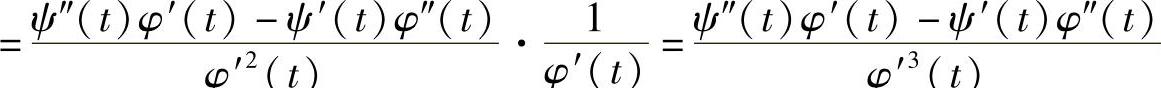例5 求由方程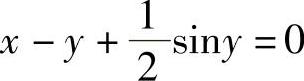
所确定的隐函数y的二阶导数
.
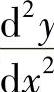解 应用隐函数的求导方法，得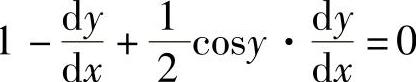
，于是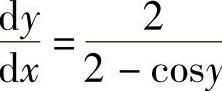
.
上式两边再对x求导得
有关高等数学（上、下册）的文章
- 详细阅读
-
参数方程导数求解方式或者函数导数：参数方程求详细阅读
1）参数方程确定的函数的导数有时函数由参数方程来表示更方便且简单，如π）表示以R为半径、原点为圆心的上半圆周曲线.星形线的直角坐标方程为其参数方程为显然星形线的参数方程更为简单.一般地，设参数方程若t∈（α，β）时，x＝x（t），y＝y（t）都有连续的导数，且x′（t）≠0，可以证明x＝x（t）必有单值反函数t＝t（x），代入y＝y（t）中，得y＝y［t（x）］，因此在所给条件下，参数方程确定了y......
2023-11-19
-
高阶导数计算方法及例题详细阅读
y＝abxn即特别地，在式中取b＝1，有在式中取a＝e，有再在上式中取b＝1，有例3求y＝（1＋x）μ（μ∈R）的n阶导数.解当μN＋，则y′＝μ（1＋x）μ－1y″＝μ（μ－1）（1＋x）μ－2…......
2023-11-19
-
高等数学上册：隐函数导数详细阅读
1）隐函数求导法（1）隐函数的导数一般地，如果方程F（x，y）＝0在一定条件下，当x在某区间内任取一值时，相应地总有满足这个方程的唯一的y值存在，那么，就称方程F（x，y）＝0在该区间上确定了一个隐函数y＝y（x）.把一个隐函数化为显函数，称为隐函数的显化.例如方程x2＋2y＝1确定的函数可显化为但有些隐函数的显化是困难的，甚至是不可能的.而在实际问题中，往往需要计算隐函数的导数，那么能否对隐函数......
2023-11-19
- 详细阅读
-
《高等数学基础》MATLAB：积分求解详细阅读
一、求积分求积分由函数int来实现.该函数的一般调用格式为：int（s）：没有指定积分变量和积分阶数时，系统按默认变量对被积函数或符号表达式s求不定积分.int（s，v）：以v为自变量，对被积函数或符号表达式s求不定积分.int（s，v，a，b）：求定积分运算.a，b分别表示定积分的下限和上限.该函数求被积函数在区间[a，b]上的定积分.a和b可以是两个具体的数，也可以是一个符号表达式，还可以是无......
2023-11-20
-
高等数学基础：偏导数的概念详细阅读
一、偏导数的概念【知识点回顾】y=f（x）在x=x0处导数的定义：设函数y=f（x）在点x0的某一邻域内有定义，当自变量x在x0处有增量Δx（x+Δx也在该邻域内）时，相应地，函数有增量Δy=f（x0+Δx）-f（x0），若Δy与Δx之比有当Δx→0时极限存在，则称这个极限值为y=f（x）在x0处的导数.记为基本初等函数的导数公式如下：（1）（c）′=0（c为常数）（2）（xμ）′=μxμ-1(......
2023-11-20
- 详细阅读
相关推荐