首页理论教育高等数学：无穷小与无穷大

高等数学：无穷小与无穷大

2023-11-22 理论教育版权反馈

【摘要】：一、无穷小定义1.18 若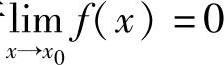，则称f（x）是当x→x0时的无穷小量，又称无穷小.在上述定义中，将x→x0换成x→x0+，x→x0-，x→+∞，x→-∞，x→∞以及n→∞，可定义不同形式的无穷小.例如：当x→0时，函数x3，sinx，tanx都是无穷小.当x→+∞时，函数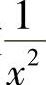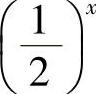，，都是无穷小.当n→∞时，数列，，都是无穷小.无穷小是极限为零的变量，而不是“很小的数”.除零之外的任何常数，无论它的绝对值怎么小

一、无穷小

定义1.18 若，则称f（x）是当x→x₀时的无穷小量，又称无穷小.

在上述定义中，将x→x₀换成x→x₀⁺，x→x₀^-，x→+∞，x→-∞，x→∞以及n→∞，可定义不同形式的无穷小.例如：

当x→0时，函数x³，sinx，tanx都是无穷小.

当x→+∞时，函数，，都是无穷小.

当n→∞时，数列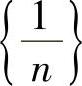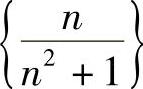，，都是无穷小.

无穷小是极限为零的变量，而不是“很小的数”.除零之外的任何常数，无论它的绝对值怎么小，都不是无穷小.

由无穷小的定义及极限的四则运算法则，可得如下性质.

定理1.12 若函数f（x）与g（x）都是x→x₀时的无穷小，则函数f（x）±g（x）是x→x₀时的无穷小.

定理1.13 若函数f（x）是x→x₀时的无穷小，函数g（x）在x₀的某去心邻域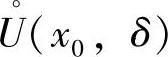有界，则f（x）·g（x）是x→x₀时的无穷小.

特别地，若f（x）与g（x）都是当x→x₀时的无穷小，则函数f（x）·g（x）也是x→x₀时的无穷小.

推论1.3 常量与无穷小的乘积仍是无穷小.

定理1.14 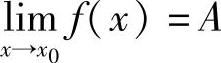的充要条件是f（x）=A+α（x），其中，α（x）是x→x₀时的无穷小.

证必要性，设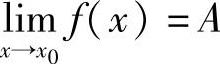，令α（x）=f（x）-A，则f（x）=A+α（x），只需证明当x→x₀时，α（x）是无穷小量.

事实上，因为_xlim，则对于任意给定的ε＞0，存在δ＞0，当0＜|x-x₀|＜δ时，有|f（x）-A|＜ε，由定义1.18可知，α（x）=f（x）-A是无穷小.

充分性，设f（x）=A+α（x），其中，α（x）（x→x₀）是无穷小，则f（x）-A=α（x）.因α（x）（x→x₀）是无穷小，则对于任意给定的ε＞0，存在δ＞0，当0＜|x-x₀|＜δ时，有|f（x）-A|=α（x）＜ε.

所以.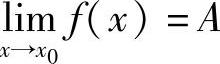

二、无穷大

定义1.19 设f（x）在x₀的某一去心邻域内有定义，若对任意给定的正数M＞0，总存在δ＞0，当0＜|x-x₀|＜δ时，有|f（x）|＞M，则称函数f（x）当x→x₀时是无穷大，表示为

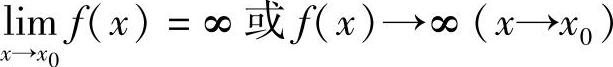
将定义中的不等式|f（x）|＞M改为f（x）＞M或f（x）＜-M，则称函数f（x）当x→x₀时是正无穷大或负无穷大.分别表示为

无穷大不是很大的数，无穷大是在随着自变量的变化过程中，绝对值无限增大的变量.

例1 证明.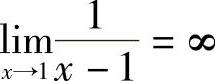

证对于任意给定的M＞0.要使，只须，取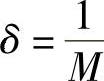，于是对于任意给定的M＞0，存在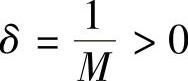，当0＜x-1＜δ时，有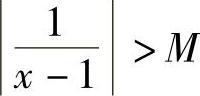，即.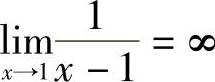

例2 证明

证对于任意给定的M＞0（M＞1），要使不等式a^x＞M成立，只要x＞log_aM，取X=log_aM，于是对于任意给定的M＞0，存在X=log_aM，当x＞X时，有a^x＞M即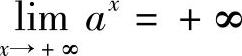.(www.chuimin.cn)

三、无穷小与无穷大的关系

定理1.15 在自变量的同一变化过程中，

1）若f（x）是无穷大，则是无穷小；2）若f（x）是无穷小，且f（x）≠0，则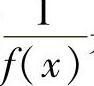是无穷大.

证只证2）.设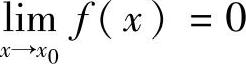，且f（x）≠0.对于任意给定的M＞0，当x→x₀时，f（x）是无穷小，则对任意的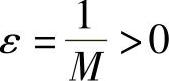，存在δ＞0，使得当0＜|x-x₀|＜δ时，有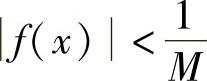，也就是.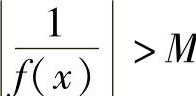

即，函数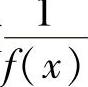当x→x₀时是无穷大.

四、无穷小的比较

当x→0时，函数x，2x，x²都是无穷小，但它们趋于0的速度却不一样.如表1-1所示：

表1-1

显然，x²趋于0的速度最快，而x与2x趋于0的速度相差不大.由此，引入无穷小的比较.

定义1.20 设α与β是在自变量的同一变化过程中的两个无穷小，且β≠0.

若，则称α是β的高阶无穷小，记为α=o（β）.

若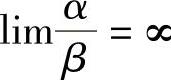，则称α是β的低阶无穷小.

若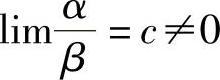，则称α与β是同阶无穷小.特别地，若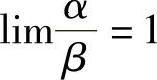，则称α与β是等价无穷小，记为α～β.

例3

1）因为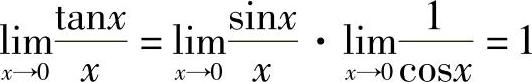，所以tanx～x.

2）因为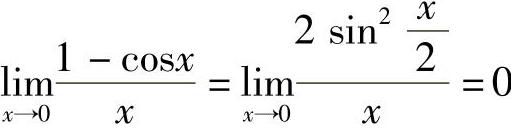，所以1-cosx是x的高阶无穷小.

3）因为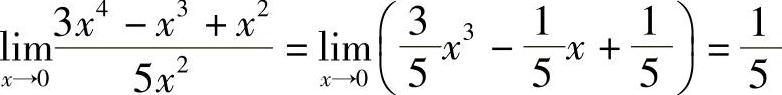，所以两者是同阶无穷小.

定理1.16 若α～α′，β～β′，且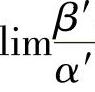存在，则.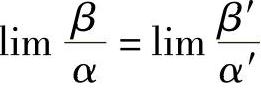

证 .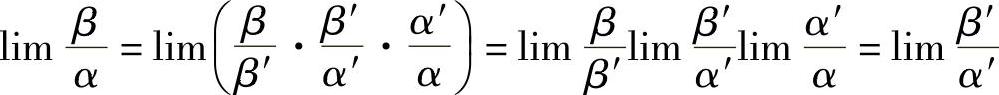

例4 求.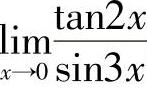

解当x→0时，tan2x～2x，sin3x～3x，所以.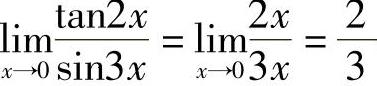

例5 求.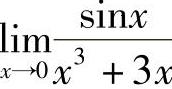

解当x→0时，sinx～x，而x³+3x与它本身显然是等价的，所以.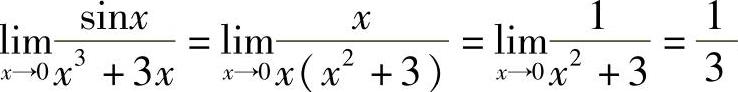

当x→0时，常见的等价无穷小有sinx～x，arcsinx～x，tanx～x，arctanx～x，

ln（1+x）～x，e^x-1～x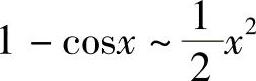，，（1+x）^m-1～mx.