定理1(1)(2)(3)如果B≠0,则证(1)因为所以当x→□时,f(x)-A与g(x)-B均为无穷小,因而这两个无穷小的代数和[f(x)-A]±[g(x)-B]=[f(x)±g(x)]-[A±B]仍是当x→□时的无穷小,因此(2)由题设,可令则f(x)·g(x)=[A+α(x)]·[B+β(x)]=AB+[A·β(x)+B·α(x)+α(x)·β(x)]由无穷小的性质可知,上式中的函数A·β......
2023-11-19
一、四则运算法则
定理1.9 若 ,
, ,则1)
,则1)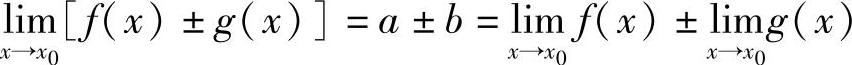 ;2)
;2) ;3)当b≠0时,
;3)当b≠0时,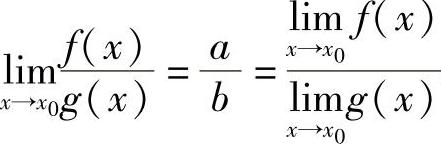 .
.
证 只证2).
因为 ,存在δ0>0,当0<|x-x0|<δ0时,|f(x)|≤M.
,存在δ0>0,当0<|x-x0|<δ0时,|f(x)|≤M.
对于任意给定的ε>0,存在δ1>0,当0<|x-x0|<δ1时,有f(x)-a<ε成立;
对于任意给定的ε>0,存在δ2>0,当0<|x-x0|<δ2时,有g(x)-b<ε成立;
取δ=min{δ0,δ1,δ2},则当0<|x-x0|<δ时,有
|f(x)·g(x)|-ab=|f(x)·g(x)-f(x)b+f(x)b-ab|≤|f(x)|·|g(x)-b|+|b||f(x)-a|<Mε+|b|ε=(M+|b|)ε
即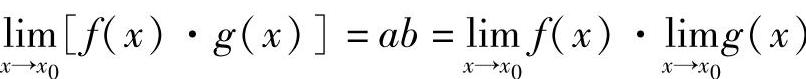 .定理的1)、2)可推广到有限多个函数的和或积的情形.作为2)的特殊情形,有
.定理的1)、2)可推广到有限多个函数的和或积的情形.作为2)的特殊情形,有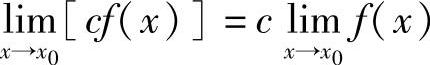 (c为常数),
(c为常数),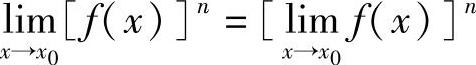 .
.
例1 求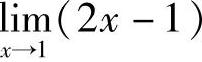 .
.
解 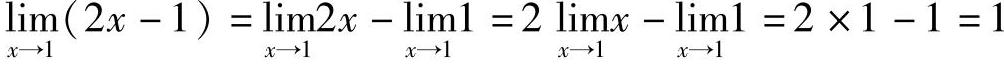 .
.
例2 求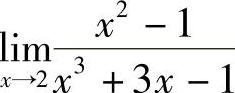 .
.
解  .
.
从例1和例2可以看出,对于有理整函数(多项式)或有理分式函数(分母不为零),求其极限时,只要把自变量x的极限值代入函数就可以了.
对于多项式函数
对于有理分式函数 ,其中,P(x)和Q(x)均为多项式,且Q(x0)≠0.
,其中,P(x)和Q(x)均为多项式,且Q(x0)≠0.
则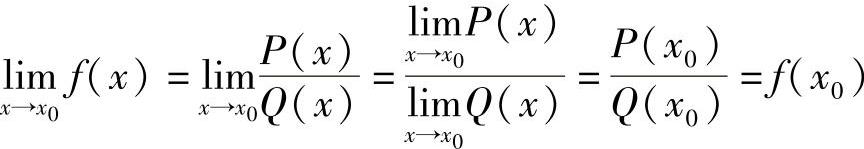 .
.
例3 求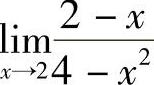 .
.
解 当x→2时,x≠2,x-2≠0.所以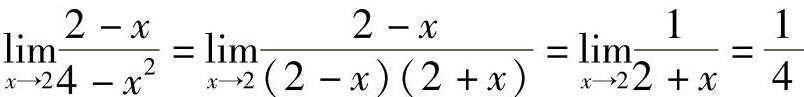 .
.
例4 求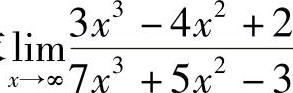 .
.
解 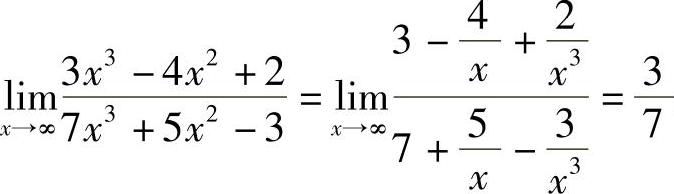 .
.
例5 求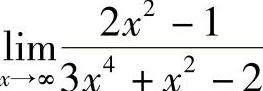 .
.
解  .
.
若Q(x0)=0,则不满足定理条件,不能用上述结论,需采用其他手段.
例6 求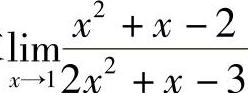 .(www.chuimin.cn)
.(www.chuimin.cn)
解 当x→1时,分子、分母均趋于0,因为x≠1,约去公因子(x-1),所以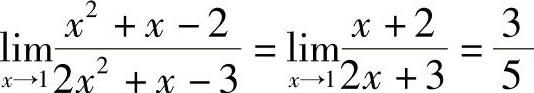 .
.
例7 求 .
.
解 当x→-1时,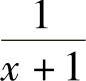 和
和 的极限不存在,故不能直接用定理1.9的结论,但当x≠-1时,
的极限不存在,故不能直接用定理1.9的结论,但当x≠-1时,
所以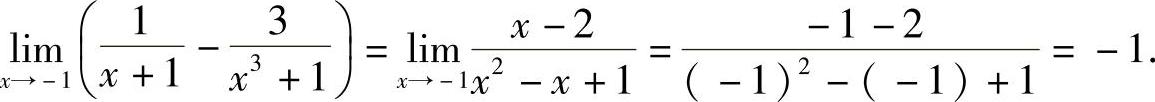
例8 求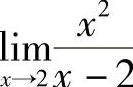 .
.
解 当x→2时,(x-2)→0,故不能直接用定理1.9的结论,由于x2→4,可以考虑: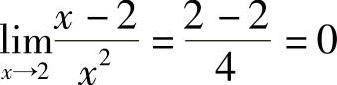 ,由此可知
,由此可知 在x→2时,函数值无限增大,把它记为
在x→2时,函数值无限增大,把它记为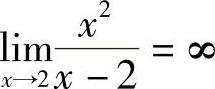 .
.
例9  .
.
解  .
.
例10 设a0≠0,b0≠0,m、n为自然数,则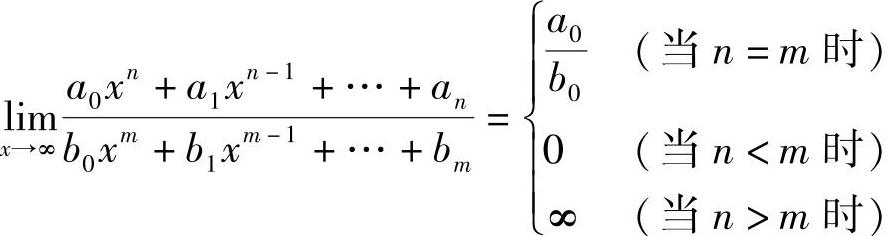
证 当x→∞时,分子、分母极限均不存在,故不能用定理1.9的结论,先变形:.
例11 求 .
.
解 当n→∞时,这是无穷多项相加,故不能直接用定理1.9的结论,先变形: .二、复合函数的极限运算法则
.二、复合函数的极限运算法则
定理1.10 设 ,且当x满足0<|x-x0|<δ1时,φ(x)≠a,又
,且当x满足0<|x-x0|<δ1时,φ(x)≠a,又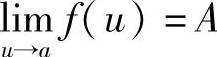 ,则有
,则有
证 由 ,对于任意给定的ε>0,存在η>0,当0<u-a<η时,有
,对于任意给定的ε>0,存在η>0,当0<u-a<η时,有
|f(u)-A|<ε
又因为 ,则对上述η>0,存在δ2>0,使得当0<|x-x0|<δ2时,有
,则对上述η>0,存在δ2>0,使得当0<|x-x0|<δ2时,有
|φ(x)-a|<η
取δ=min{δ1,δ2},则当0<|x-x0|<δ时,有
0<|φ(x)-a|=|u-a|<η
故|f(φ(x))-A|=|f(u)-A|<ε
结论成立.
若定理中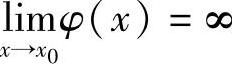 ,类似可证
,类似可证 .
.
例12 求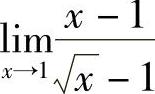 .
.
解 令 ,则
,则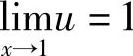 ,从而
,从而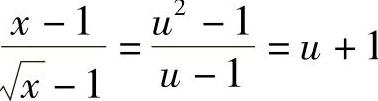 1,故
1,故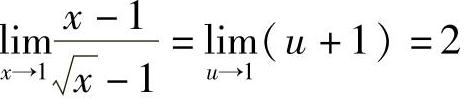
有关高等数学(上、下册)的文章

定理1(1)(2)(3)如果B≠0,则证(1)因为所以当x→□时,f(x)-A与g(x)-B均为无穷小,因而这两个无穷小的代数和[f(x)-A]±[g(x)-B]=[f(x)±g(x)]-[A±B]仍是当x→□时的无穷小,因此(2)由题设,可令则f(x)·g(x)=[A+α(x)]·[B+β(x)]=AB+[A·β(x)+B·α(x)+α(x)·β(x)]由无穷小的性质可知,上式中的函数A·β......
2023-11-19

由函数的和、差、积、商的求导法则,结合公式(2-46)可推得相应的微分运算法则,为了便于对照,列于表2-2中.表2-2函数的求导法则与微分法则下面仅以乘积的微分法则为例加以证明.由函数微分公式(2-46),有d(uv)=(uv)′dx=(u′v+uv′)dx=u′dx·v+u·v′dx=vdu+udv因此d(uv)=vdu+udv其他法则均可类似证明.请读者自证.下面讨论复合函数的微分.设函数y......
2023-11-19

通常,求极限的问题比较复杂,仅凭定义来求极限是不能解决问题的.为此,我们介绍极限的运算法则,在某些场合这些法则为计算极限提供了方便.一般地,我们有以下结论:注:以上法则(1)(2)可推广至有限个数列的情形,但不能推广到无限个数列的情形.利用定理1和一些已知数列极限,可以把复杂的数列极限的计算问题转化为简单的数列极限的计算问题.例5求下列数列的极限:注:以上两小题满足极限的四则运算,如果不能直接应......
2023-11-17

1)连续函数的四则运算法则函数的连续性是由函数的极限来定义的,所以根据极限的四则运算法则,可得下面的连续函数的四则运算法则.定理1若函数f(x)与g(x)都在点x0处连续,则函数f(x)±g(x),f(x)·g(x)都在点x0处连续,若再增加条件g(x0)≠0,则也在点x0处连续.证设函数f(x),g(x)都在点x0处连续,所以由极限的加、减、乘运算法则,可得即f(x)±g(x),f(x)·g......
2023-11-19

利用函数极限的定义,可得下列极限的性质.1)唯一性定理2若存在,则极限唯一.证(反证法)假设极限不唯一,则存在两个不相等的常数a,b,使得均成立.不妨设b>a,由于取则δ1>0,当x满足0<|x-x0|<δ1时,恒有即又由于仍取则δ2>0,当x满足0<|x-x0|<δ2时,恒有即取δ=min{δ1,δ2},则当x满足0<|x-x0|<δ时,上面(1-5)、(1-6)两式均成立,但这是不可能的.......
2023-11-19

对于给定的数列{xn},我们讨论当项数n无限增大时(记作n→∞),对应项的变化趋势.观察上面的四个数列,容易看出,当n→∞时,数列趋于1;数列各项的值在数1的两侧来回交替着变化,且越来越接近1;数列{2n-1}越来越大,无限增大;数列{1-(-1)n}各项的值永远在0与2之间交互取得,而不与某一数接近.如果当n→∞时,数列的项xn能无限接近于某个常数A,则称这个数列为收敛数列,常数A称为当n→∞时......
2023-11-19

若在自变量的某个变化过程中,函数f(x)不能与某个确定的值无限接近,则f(x)在此变化过程中的极限不存在.极限不存在的具体情况可能很复杂,下面举出几种常见的类型.1)当x→x0或x→∞时,函数的绝对值无限增大如果在x的某一变化过程中,对应函数f(x)的绝对值|f(x)|无限增大,那么f(x)就不可能向某一定值逼近,因此f(x)在此变化过程中的极限就不存在.这时,虽然极限不存在,但由于|f(x)|是......
2023-11-19
相关推荐