混沌系统控制及其在信息安全中的应用研究概况

2023-11-22 理论教育版权反馈

【摘要】：由于混沌的奇异特性，尤其是对初始条件扰动极端敏感的特性，使得人们一度认为混沌是不可控的。该方法开创了混沌控制的先河，人们称之为OGY方法[5]。这些开创性的工作激发起了人们对混沌控制理论与实验研究的浓厚兴趣，并向世人展现了诱人的应用前景。由混沌运动的遍历性，系统的状态将再次回到xf的邻域，控制系统重新启动。

目前，人们对混沌控制的理解，从广义上说是人为并有效地通过某种方法控制混沌系统，使之发展到实际所需要的状态。主要有以下几个方面：

1）在混沌有害时，成功地抑制混沌或消除混沌；

2）在混沌有利时，利用混沌来产生所需要的具有某些特点的混沌运动，甚至产生某些特定的混沌轨道；

3）在系统处于混沌状态时，通过外部控制产生出人们所需要的各种输出。

由于混沌的奇异特性，尤其是对初始条件扰动极端敏感的特性，使得人们一度认为混沌是不可控的。直到1990年美国物理学家Ott，Grebogi和Yorke所做的开创性工作，提出一种比较系统和严密的参数微扰方法，成功地将混沌系统镇定在不稳定的周期轨道上。该方法开创了混沌控制的先河，人们称之为OGY方法[5]。同年，美国海军实验室的Pecora和Carroll提出了混沌同步的概念及方法[6]。这些开创性的工作激发起了人们对混沌控制理论与实验研究的浓厚兴趣，并向世人展现了诱人的应用前景。下面对一些有代表性的成果和新进展做一些简要介绍和评述。

1.OGY控制方法及其改进方法

OGY控制方法[4，5]充分利用了混沌运动的特点，在控制方面表现出许多特色，直到今天，OGY方法的控制思想仍然为控制混沌的重要策略。它建立在混沌吸引子中嵌有无数条不稳定的周期轨道的理论基础之上，利用混沌运动对很小的参数扰动敏感和混沌运动的遍历性，给混沌运动系统的参数施加含时小扰动，把在无穷多不稳定周期轨道中所期望的那个不稳定周期轨道稳定住，使系统处于不动点或做有规律的周期运动。具体方法以一个n维离散的混沌系统来说明OGY方法的实现过程。设系统的数学模型为

式中，p是系统参数；x∈Rn是系统状态。控制参数p可以在p0附近变化，不妨令p0=0。当参数p从p0变到p时，不动点从xf（p0）变到xf（p）。

在不动点xf（0）附近对式（1-10）描述的混沌系统线性化，得到一个映射

M是n×n的Jacobi矩阵，用ru和rs代表M的不稳定和稳定特征值，。在系统模型不知道的情况下，可以通过实验数据来确定xf（p），M，G，ru和rs。MEu=ruEu，MEs=rsEs，Eu和Es是M的不稳定和稳定的单位特征向量，Fu和Fs代表与之正交的向量，即Eu·Fu=Es·Fs=1，Eu·Es=Es·Eu=0。式（1-12）可以表示为

由式（1-11），可以把式（1-13）改写为

xn+1=pG+xf（0）+（ruEu·Fu+rsEs·Fs）（xn-pG-xf（0）（p在0附近变化）通过p的扰动使xn+1落在不动点xf（0）附近的稳定流型上，即Fu·xn+1=0。

因为p与xn有关，每步迭代要计算p，控制由调节p的值来实现，使混沌系统的状态稳定到不动点xf（0）。为使式（1-11）成立，需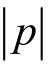 pagenumber_ebook=23,pagenumber_book=14 ＜p*，p*充分小，如＞p*，令p=0，这时系统再次进入混沌运动状态。由混沌运动的遍历性，系统的状态将再次回到xf（0）的邻域，控制系统重新启动。

OGY方法无须知道系统的动力学模型，且对离散系统和可离散化的连续系统均适用。同时，该法每次映射迭代所需的计算量及所需的参数变化都很少。而且在延迟坐标下达到控制目标后，嵌套在混沌吸引子中的不稳定周期轨道只有微小变化。该方法的缺点是只适用于离散混沌系统及可以用庞加莱映射表征的连续混沌系统，并且通常情况下只能控制低周期轨道。这些都限制了该方法的使用范围。

后来，Ott、Grebogi又与Romeiras、Daywansa合作，将OGY方法的基本思想与控制系统理论中的极点配置技术相结合，控制了高周期态和高维系统的非周期轨道，但实际上控制效果也不理想。为了有效控制混沌吸引子中的高周期轨道，1991年俄亥俄州大学的Hunt提出了OPF（Occasional Propotional Feedback）方法[26]。该方法是一种分析技术，具有很大的优点，它不仅只需小微扰就容易控制低周期态，而且通过调整信号限制窗口的宽度及反馈信号的增益量，能够有效地控制高周期轨道。OPF技术的另一个优点是控制器所需的信息可直接从测量混沌行为得到，能够快速控制混沌。美国海军实验室基于OPF技术开发了一种跟踪法，应用于激光系统，把激光装置的输出功率提高了15倍。

OGY方法的贡献不仅在控制方法上，而更重要的是在观念上。它使人们重新审视混沌系统，正是OGY方法的提出，带动了混沌研究的热潮。(www.chuimin.cn)

2.连续反馈控制方法

针对OGY控制方法的不足，德国科学家Pyragas提出了两种适用于连续混沌系统的方法[27，28]：外力反馈控制法和延迟反馈控制法。其基本思想都是考虑混沌系统的输出与输入信号之间的自反馈耦合，这两种方法都可以实现对混沌吸引子中不稳定周期轨道的稳定控制。

外力反馈控制法从系统外面注入一个强迫信号，用以与系统的输出量相比较，给出控制信号。与OGY方法的不同在于，该方法不受必须靠近轨道的限制，可以在任何时候加入微扰来控制。假设外力反馈描述的受控系统的动力学方程为

式中，y是输出变量，矢量x为系统的其余状态变量，F（t）为微扰的控制信号，当无控制时，即F（t）=0，系统应处于混沌状态。假设将系统控制到混沌吸引子中某个周期轨道yi（t）。为此首先设计一个的周期信号发生器来产生所需的周期信号yi（t），或产生的信号正比于yi（t），然后把目标信号yi（t）与输出信号y（t）之差D（t）=yi（t）-y（t）作为控制信号，即

反馈到（1-15）式中。式中K为可调节的控制强度。当y（t）=yi（t）时，F（t）的引入并不改变相应的不稳定周期轨道。当y（t）≠yi（t）时，通过调节控制强度K就可以到达稳定控制目的，当到达控制时F（t）=K[y（t）-yi（t）]=0，反馈控制不起作用。

Pyragas采用外力反馈方法对Rössler系统、Lorenz系统和Duffing系统进行了控制，都取得了满意效果。但该方法是需先确定目标轨道的，这样需要对系统的输出信号进行大量即时的采集与分析。为了解决这一问题，Pyragas同时又提出了延迟反馈控制方法。这种方法的微扰形式为

即以y（t-τ）取代外部信号yi（t），τ为时间延迟，这里应选取τ为不稳定周期轨道的周期。其他做法与以上的外力延迟反馈控制方法相似，通过调节K和D（t）的值来达到控制目标。当延迟反馈与原系统的轨道发生共振，并且稳定了这些轨道时，y（t-τ）=y（t），即控制信号F（t）=0；当被控制系统稳定到了周期轨道，但F（t）≠0时，这时的周期轨道不是原系统的固有的，而是产生了新的动力学行为。

延迟反馈方法利用系统本身输出信号的一部分并经过一定的时间延迟后，再与原来输出信号相减，作为控制信号反馈到系统中去，使系统在自动寻找原混沌系统不稳定周期轨道的同时实现混沌控制。Pyragas在数值模拟和实验上均证实了延迟反馈方法的有效性，并考虑了噪声的影响，其鲁棒性和抗噪声能力要优于OGY方法。后来，一些学者对连续反馈方法在多变量方面又进行了改进和补充[29，30]。

3.迁移与传输控制方法

迁移与传输控制的基本思想是假定目标轨道满足于给定动力学系统相同的数学方程，然后把两个方程叠加起来，由此迫使被控系统的混沌状态转移到目标轨道之中[31]。该控制方法是一种开环控制，设计和使用都非常简单，只要求知道系统的初始状态，在控制实施中不再需要系统的状态，而且适用于连续动力学系统和离散系统。缺点是，需要预先知道系统的特性，特别是关于吸引子空间的收敛区域。对目标动力学的收敛取决于初始条件，或者传输的流域，所以不能任意选择控制目标。

4.传统控制理论在混沌控制中的应用

OGY法、OPF技术和连续反馈控制方法等微扰方法，并不是传统的控制理论。它们实现控制的共同机理是变系统原来正的Lyapunov指数为负值，从而实现被控系统从不稳定到稳定的转变。传统的控制方法已有很长的研究历史，并且已建立了很多行之有效的理论和方法。因此，不少学者尝试采用各种传统的控制手段来实现混沌控制。常规的线性和非线性反馈控制已经成功地用来控制混沌系统[32，33]。线性和非线性反馈控制主要是基于Lyapunov理论或反馈线性化等补偿理论，它们都能够稳定跟踪参考输入或抑制不确定性干扰的不稳定系统，将系统稳定到不动点或周期轨道。缺点是必须知道被控系统的模型和参数。

在许多实际的情况下，被控混沌系统的模型或参数很难精确知道。为此，一些学者将自适应控制理论应用于混沌控制。Bernardo基于Lyapunov理论，设计了模型参考的自适应的控制方法[34]，该方法可以适宜一大类混沌系统的控制。Ge等[35]将被控的混沌系统转换成非自治的严格反馈形式的非线性系统，利用一种构成反馈控制和李雅普诺夫函数的系统设计方法，提出了另一种采用模型参考自适应控制方法。在参数未知Duffing振荡器的仿真表明，控制效果良好。另外，基于参数估计的自适应控制、基于反馈线性化方法的自适应控制或自适应方法和其他传统控制相结合的控制方法也相继被用于混沌控制中[36-38]。

近年来，人们也将智能控制方法引入到混沌控制中。Oscar利用模糊控制策略对Chua氏混沌电路进行了快速稳定控制[39]。Chen等在混沌系统的输入输出数据能利用的情况下，应用模糊模型对不确定混沌系统进行了辨识和控制[40]。Lin提出了一种基于遗传算法的再励学习神经网络控制器，在不知道系统的平衡点和输入—输出数据的情况下，将系统稳定到高周期轨道上[41]。

除了以上控制方法外，混沌控制还有许多其他方法[42-44]，在此很难一一列举。这些方法试图从不同角度来解决混沌控制问题，每一种方法都有其优点，也有其适用范围和限制，因此值得深入研究。

混沌系统控制及其在信息安全中的应用研究概况

相关推荐