一些学者在著名的3维自治混沌系统和统一混沌系统基础上产生了4维超混沌系统[263-266]。然而由于超混沌的动力学行为比较复杂,而且缺乏统一的理论基础,产生超混沌系统仍然是一项比较有挑战的研究。不仅用Lyapunov指数谱、分岔分析和相图分析了这个新系统的动力学行为,而且设计了这个系统的电路,通过Multisim软件进行了实验模拟。针对这个3维自治混沌系统,关于怎样构建控制项来产生超混沌,给出了一种设计方法,并进行了实例论证。......
2023-11-22
混沌是非线性系统所呈现出来的一种高度复杂的动力行为,但并不是任何一个非线性系统都具有混沌行为,因此如何判断给定的一个非线性系统具有混沌行为、如何将混沌行为进行数学上的定量化说明是混沌研究中几个无法避免的问题。下面介绍一下目前研究混沌运动的主要方法[4,23]。
1.直接观测法
该方法是依据混沌动力系统的方程,结合仿真技术,画出相空间中相轨迹随时间的变化图,以及状态变量随时间变化的历程图。通过对比、分析和综合加以确定解的分岔和混沌现象。在相空间中,周期运动对应封闭曲线,混沌运动对应一定区域内随机分离的永不封闭的轨迹,即奇怪吸引子。利用此方法可确定分岔点和普适常数,是复杂工程问题混沌研究的重要方法。
2.Poincáre截面法
Poincáre截面法的基本思想是在多维相空间(x1,dx1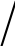 dt,x2,dx2
dt,x2,dx2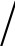 dt,…,xn,dxn
dt,…,xn,dxn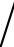 dt)中适当选取一个截面,在此截面上某一对共轭变量如(x1,dx1
dt)中适当选取一个截面,在此截面上某一对共轭变量如(x1,dx1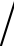 dt)取固定值,称此截面为庞加莱截面(Poincáre Section)。观察运动轨迹与此截面的截点,设它们依次为P0,P1,…,Pn。原来相空间的连续轨迹在Poincáre截面上便表现为一些离散点之间的映射Pn+1=TPn,由此可得到关于运动特性的信息。若不考虑初始阶段的暂态过渡过程,仅考虑Poincáre截面的稳态图像,则当Poincáre截面上只有一个不动点或少数离散点时,运动是周期的;当Poincáre截面上是一封闭曲线时,运动是准周期的;当Poincáre截面上是成片的密集点,且有层次结构时,运动便是混沌的。
dt)取固定值,称此截面为庞加莱截面(Poincáre Section)。观察运动轨迹与此截面的截点,设它们依次为P0,P1,…,Pn。原来相空间的连续轨迹在Poincáre截面上便表现为一些离散点之间的映射Pn+1=TPn,由此可得到关于运动特性的信息。若不考虑初始阶段的暂态过渡过程,仅考虑Poincáre截面的稳态图像,则当Poincáre截面上只有一个不动点或少数离散点时,运动是周期的;当Poincáre截面上是一封闭曲线时,运动是准周期的;当Poincáre截面上是成片的密集点,且有层次结构时,运动便是混沌的。
3.相空间重构法
对系统在相空间的表现进行分析是很简便且很直观的方法。但是组成相平面或相空间至少需两个或两个以上变量的时间序列数据,而通常测得的往往只是一个变量的时间序列。但是可以想象,一个变量随时间的变化是由整个系统的运动规律支配的,因此单一变量的时间序列应该隐含着整个系统的运动规律。这时可利用所测得的时间序列重构相空间。重构相空间维数即嵌入维数应满足m≥2n+1,其中n为相空间的真实维数。设测得的时间序列为{x(k),k=1,2,…,n},适当选取一时间延迟量τ,即重构相空间的间距,其中τ为采样周期的整数倍,取x(k),x(k+τ),x(k+2τ),…,x(k+(m-1)τ)为坐标抽,画出重构相空间轨迹。
上述重构吸引子的过程相当于将时间序列x(k)映射到m维的欧式空间Rm中,并希望Rm空间中的点能保持原有未知吸引子的拓扑特性。相空间重构法虽然是用一个变量在不同时刻的值构成相空间,但动力系统的一个变量的变化自然跟此变量与系统的其他变量的相互关系有关,即此变量随时间的变化隐含着整个系统的动力学规律。因此,重构相空间的轨线也反映了系统状态的演化规律。对于定态,通过这种方法得到的结果仍是一定点;对于周期运动,结果是有限个点;而对于混沌系统,所得到的结果则是一些具有分布形式或离散结构的离散点。
4.功率谱分析法
功率谱分析是研究混沌的一个重要手段。功率谱是单位频率上的能量,它能反映出功率在频率上的分布情况。假定已经获得了按等时间间隔Δt的时间序列x(k)(k=1,2,…,N),对这个序列加上周期边界NN+j=Nj,然后计算自关联函数:
再对Cj作离散傅里叶变换,计算其傅里叶系数:
Pk代表第k个频率分量对xi的贡献,这就是功率谱的本来的意义[1]。实际计算时可直接对时间序列按下式进行快速傅里叶变换:
则功率谱定义为![]()
功率谱分析法可有效地判断系统的运动性质。例如,对频率为f的周期系统的功率谱在频率f及其高次谐波2f, 3f, …处有δ 函数形式的尖峰。每个尖峰的高度指示了相应频率的振动强度。特别当发生分岔时,功率谱将改变它的特征。基频为f1, f2, …, fk的准周期系统的功率谱在f1, f2, …, fk及其线性组合处有δ 函数形式的尖峰。对于混沌系统,尽管其功率谱仍可能有尖峰,但它们多少会增宽一些(不再相应于分辨率),而且功率谱上会出现宽带的噪声背景。可见功率谱分析对周期和准周期现象的识别以及研究它们与混沌态的转化过程是非常有力的。
5.关联维数分析法(www.chuimin.cn)
维数是空间和客体的重要的几何特征。在状态空间中维数反映了描述该空间中运动所需的变量个数,而在吸引子中维数则说明了刻划吸引子所必需的信息量。混沌的奇怪吸引子具有不同于通常几何形状的无限层次的自相似结构。分维数可对吸引子的几何特征以及集于吸引子上的轨道随时间的演化情况进行数量上的描述。分维数有多种定义,其中Grassberger和Procaccia在1983年提出了一种易于从实验数据中提取分维数即关联维数的算法[18]。其算法如下:
首先,计算n维状态空间中任意两点间距离小于r的概率,如下式所示:
式中,M为数据点的数目,r为n维小球的半径。凡是距离小于给定正数r的矢量,称为有关联的矢量。这里的H(·)是Heaviside函数
r的值取得适当,C(r)会随着r的增大而呈指数倍迅速增加。则关联维数定义为
在计算中随着嵌入维数d变化,双对数lnC(r)-lnr图曲线束中,互相平行的直线段的斜率,就是关联维数D2。维数越大,说明关联程度越低,系统复杂程度越高。
6.Lyapunov指数分析法
目前在表征混沌运动方面,显示出重大意义的统计特征值之一的,就是Lyapunov指数,它是相空间中相近轨道的平均收敛性或平均发散性的一种度量。若Lyapunov指数小于零,表示相体积收缩,运动稳定,且对初始值不敏感;若Lyapunov指数等于零,则对应临界状态,即稳定的边界;若Lyapunov指数大于零,表示相邻轨道发散,长时间行为对初值十分敏感,运动呈混沌状态。
混沌系统由相空间中的不规则轨道奇怪吸引子来描述。奇怪吸引子的一个明显特征就是吸引子邻近点的指数离析。因为相空间中的点表示整个物理系统,所以邻近点的指数离析意味着初始状态完全确定的系统在长时间情况下,会不可避免地发生变化,这种行为就是系统对初始条件具有敏感依赖性的反映。而引入的Lyapunov指数恰可定量表示奇怪吸引子的这种运动状态。
对于n维相空间中的连续动力学系统,考察一个无穷小n维球面的长时间演化。由于流的局部变形特性,球面将变为n维椭球面。第i个Lyapunov指数按椭球主轴长度pi(t)定义为
式(1-8)表明Lyapunov指数的大小表示相空间中相近轨道的平均收敛或发散的指数率。Lyapunov指数是很一般的特征数值,它对每种类型的吸引子都有定义。对于n维相空间有n个实指数,故也称为谱,并按其大小排列,一般令λ1≥λ2≥λ3…≥λn。一般说来,具有正和零Lyapunov指数的方向,都对支撑起吸引子起作用,而负Lyapunov指数对应着收缩方向。这两种因素对抗的结果就是伸缩与折叠操作,这就形成奇怪吸引子的空间几何形状。因此,对于奇怪吸引子而言,其最大Lyapunov指数λ1为正的(另外也至少有一个Lyapunov指数是负的),并且Lyapunov指数λ1越大,系统的混沌性越强;反之亦然。
本书采用了Wolf提出的计算最大Lyapunov指数λ1的算法——长度演化法[20],其算法如下:
设时间序列X(t),利用时间延迟法构造m维相空间,空间中的每一点是由{X(t),X(t+τ),…,X(t+(m-1)τ)}给出的。首先找出距初始点{X(t0),X(t0+τ),…,X(t0+(m-1)τ)}最近的点,用L(t0)表示这两点间的距离。到t1时刻L(t0)已演化成L′(t1),这时再按以下两原则寻找一个新的数据点:它与演化后基准点的距离L(t1)很小;且L(t1)与L′(t1)的夹角很小。这个过程重复进行,直到穷尽所有的数据点。则λ1为
式中,N是长度元演化的总次数。至λ1趋于某一稳定值时,计算才算成功。
有关混沌系统控制及其在信息安全中的应用的文章

一些学者在著名的3维自治混沌系统和统一混沌系统基础上产生了4维超混沌系统[263-266]。然而由于超混沌的动力学行为比较复杂,而且缺乏统一的理论基础,产生超混沌系统仍然是一项比较有挑战的研究。不仅用Lyapunov指数谱、分岔分析和相图分析了这个新系统的动力学行为,而且设计了这个系统的电路,通过Multisim软件进行了实验模拟。针对这个3维自治混沌系统,关于怎样构建控制项来产生超混沌,给出了一种设计方法,并进行了实例论证。......
2023-11-22

混沌是非线性动态系统所特有的一种运动形式,它既是普遍存在又是极具复杂性的现象。混沌学是随着现代科学技术的迅猛发展,尤其是在计算机技术的出现和普遍应用的基础上发展起来的,并得到人们广泛的关注和研究。这一结果被认为是动力系统中具有混沌特征的第一征兆。在这一时期,混沌学作为一门新兴的科学正式诞生。这些实验研究不仅丰富了混沌理论,而且极大地拓宽了混沌的应用领域和范围。......
2023-11-22

从前面的混沌控制和同步的介绍中,可以看出经过十多年的研究,国内外学者已经提出了很多混沌控制和同步的方法,并已成功地进行应用尝试。在如何保持原系统的运动特性,发掘和利用混沌系统的特征方面还有待进一步深入的研究。因此,缺少普遍适用的严密的理论去分析和研究混沌系统的控制策略。因此,很多混沌系统的控制策略缺乏对鲁棒性问题的考虑,在实际情况下,难以应用。......
2023-11-22

对密码进行分析的尝试称为攻击。最常用的密码分析攻击方法有以下几类。在选择明文攻击中,密码分析者还可以选择一大块被加了密的明文。例如,密码分析者存取一个防篡改的自动解密盒,密码分析者的任务是推出密钥。......
2023-11-22

在上述研究的基础上,本章研究了一类具有多扇区非线性输入不确定混沌系统的追踪控制问题,利用线性分离和滑模控制相结合的方法,设计了滑模变结构控制器,从理论上证明了该控制器的有效性。并通过对具有多扇区非线性输入的不确定Rssler系统和超混沌Chen系统的追踪混沌控制,进一步验证了该控制器的有效性。......
2023-11-22

而后,再通过数值仿真实验和计算最大Lyapunov指数来进一步验证理论分析的有效性。对这个分数阶系统分析发现,在这个新的3维系统中存在混沌的最低阶数是2.46,也发现了不同的周期行为。并且,基于拉普拉斯变换理论,设计了一个非线性反馈控制器,完成了这个分数阶混沌系统的广义投影同步控制。......
2023-11-22

混沌密码技术虽然获得了很大进展,但在发展中也出现了诸多问题:1)混沌的离散化问题。这些不利因素都是由混沌自身引起的,但目前还缺少对适合用于密码系统中的混沌映射的研究。虽然混沌密码学还存在着众多的问题,但作为一个新兴的学科,这些问题的存在是允许的和合理的,混沌密码学丰富了密码学的内容,从一个新的角度研究了数据加密技术。随着混沌密码学的进一步发展和现有问题的解决,相信它会有广阔的应用前景。......
2023-11-22

混沌理论与密码学之间存在着紧密联系[89]。因此,可用混沌映射开发新的公钥密码算法。混沌和密码学之间具有的天然的联系和结构上的一些相似,启示着人们把混沌应用于密码学领域。尽管如此,我们仍然能够利用混沌的特性来设计序列密码或分组密码,特别是对分组密码来说,利用混沌的拓扑传递性来快速地置乱和扩散明文数据,以达到改变明文统计特性的目的。......
2023-11-22
相关推荐