19世纪90年代，大卫·希尔伯特证明出一个结果，它被称为“零点定理”，这个定理用精准的术语对这一对应关系做了探讨。这就是零点定理的核心，也是代数几何成立的条件。和代数拓扑类似，代数几何的核心在于，我们已经对环的性质有了许多了解，所以把簇“翻译”成环的语言处理，要比直接处理更方便。零点定理为代数几何的建立提供了基本词典。......
2023-11-22
2页纸图解数学：以迭代重复的力量，轻松三步读懂数学
【摘要】：靠近那个点的元素——我们这时引入一个度量标准——可以被这一点吸引或排斥，与之对应地，我们称这一点为汇点或源点。在这个迭代里，0是不动点，且是汇点，因为它把附近的数字都“吸引”过去了。参考阅读//No. 7 集合论，第18页No. 9 映射，第22页No. 15 科拉茨猜想，第34页No. 74 度量空间，第152页No. 90 布劳威尔不动点定理，第184页No. 91 混沌理论，第186页右图：许多工业生产过程都会将同一个步骤不断进行迭代。
1.多维度看全
假设你要切一块面包。现在，从面包末端切下1厘米厚的一片。接着，对上一步操作得到的结果，即被切下1厘米厚的一片的面包，重复这一过程。
这是迭代在日常生活中的一个例子：不断地重复一个步骤，每一次都将上一次操作输出的结果作为输入来开启下一次操作。
从数学意义上讲，只有在映射的定义域和陪域为同一个集合时，迭代才会发生。只有这样，我们才能将映射过程不断进行下去。
该集合中有一个元素会一直保持不变，这是因为它被映射到它自身，我们称之为不动点。靠近那个点的元素——我们这时引入一个度量标准——可以被这一点吸引或排斥，与之对应地，我们称这一点为汇点或源点。
下图：迭代系统通常包含某个长期进行的过程，我们可以对其进行归类。
2.关键点梳理
给定所有的有理数构成的集合，再给定一个映射——将任何一个数指向其自身的一半。从8开始进行迭代，我们能够得到：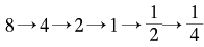
。
在这个迭代里，0是不动点，且是汇点，因为它把附近的数字都“吸引”过去了。
如果映射变为将任何一个数指向它自身的两倍，那么0还会是不动点，但它现在是源点，因为在迭代过程中，附近的数字会远离它。
参考阅读//(www.chuimin.cn)
No. 7 集合论，第18页
No. 9 映射，第22页
No. 15 科拉茨猜想，第34页
No. 74 度量空间，第152页
No. 90 布劳威尔不动点定理，第184页
No. 91 混沌理论，第186页
右图：许多工业生产过程都会将同一个步骤不断进行迭代。
3.一分钟记忆
迭代实际上是在不断地进行某个定义域和陪域相同的映射，每一次得到的输出值，都是下一次的输入值。许多自然的、技术上的日常过程都是迭代的。
有关2页纸图解数学 : 以极聪明的方式，让你三步读懂数学的文章
- 详细阅读
-
2页纸图解数学：聪明方式，轻松读懂数学详细阅读
随机游走可以模拟股价、原子甚至人类行为。因此，典型的“布朗运动”应该是以某种极其微小的幅度与极快的频率发生的方向随机的运动。为了更加贴合布朗运动的情况，我们可以将游走的步长和步与步之间的时间间隔缩短。布朗运动表示一种随机、细微、频繁的运动。......
2023-11-22
-
数学图解：学会三步读懂数学详细阅读
三角形在三维空间内的等价物是四面体。我们可以将单纯复形看作是对它所处的空间进行三角剖分，即将其分割为最简单的部分。单纯形的要点在于它们十分简单，且单纯复形可以被分解为单纯形，因此为了更好地掌握一个空间，我们可以对它进行三角剖分，这是现代几何学与拓扑学的一个基本工具。对空间进行三角剖分，可以为我们带来一个全新的、更侧重拓扑意义的视角。......
2023-11-22
-
2页纸图解数学：极简三步读懂数学详细阅读
对于空间内其他任意一点，我们从原点向它做一条直线，并在末尾处画上一个指向该点的箭头，这样一来，我们便得到了一个向量。在三维空间内，我们以自身所处的位置作为原点，用“上”“左”“前”来表示方向。......
2023-11-22
-
2页纸图解数学:三步读懂数学的极聪明方式详细阅读
一些人认为，它们证实了微积分的力量；而另一些人认为，这些事物表明了微积分这门学科的内在逻辑还存在许多漏洞。哲学家们还在持续进行着争论，而数学家们已经欣然接受了病态函数的存在。许多病态函数的图像都和这个图像类似，呈分形。如果一个病态函数导致一个矛盾出现，整个理论就会被推翻。......
2023-11-22
-
2页纸图解数学:极聪明方式，三步读懂数学详细阅读
举例来讲，我们可以将几何课本中所讲的二维空间视为一条线与另一条线相乘的结果，而想要得到我们所处的三维空间，我们只需将二维空间再“乘以”一条线。参考阅读//No. 7集合论，第18页No. 35 抽象代数，第74页No. 59 欧几里得空间，第122页3.一分钟记忆不是只有数才可以作乘法，积的观点可以被推广到任意两个集合之间。......
2023-11-22
-
2页纸图解数学:极聪明的三步读懂数学详细阅读
事实上，康托尔找到了一个可以构造出许多不同大小的无穷的方法，正好解决了我们的问题。而有了一般性的对角线论证后，我们可以证明，这一点对于无穷集合同样成立。通过不断对一个无穷集取幂集，我们可以得到一个更大无穷集的无穷序列：无穷基数。......
2023-11-22
-
最强数学图解书，让你轻松读懂数学详细阅读
接下来，试着厘清其可能导致的结果，或许就会发现矛盾。此外，如果一个命题为真，那么它所有的蕴涵命题均为真。参考阅读//No. 5 逻辑，第14页No. 14 自然数，第32页No. 27 康托尔对角线论证，第58页No. 54 病态函数，第112页No. 69 不可能的构造，第142页布尔代数的部分内容：如果一组命题为真，那么指向它的一组子命题不可能为假。如果一个命题为真，那么它所有的逻辑结果也同样为真。......
2023-11-22
相关推荐