所有能定义在V上的线性泛函的集合，构成了一个与V采用同样标量集的向量空间，我们将它写作V*。事实上，在抽象代数意义上，V*和V是同构的。因此，我们称这些线性泛函为对偶向量或者余向量，称V*为对偶空间。构造对偶空间V*的对偶空间V(**)，我们又会回到V，因此，V和V*就很像是彼此的镜像。每一个向量空间都有它的对偶空间，如果其中一个发生反变转换，那么另一个会发生共变转换，反之亦然。......
2023-11-22
张量积：从原向量空间到新向量空间
【摘要】：张量积也是一个向量空间，但我们将这个向量空间里的向量称之为张量。张量积还解决了一个特殊的代数问题。它们的张量积VW构成了一个新向量空间，所用的也是同一组标量。参考阅读//No. 7 集合论，第18页No. 8 积，第20页No. 57 向量，第118页No. 76 维度，第156页右图：张量积可以把一个不完全的线性映射转化为一个线性映射。通过取张量积，我们可以将向量空间乘在一起，得到一个新向量空间。
1.多维度看全
假如我们想要将两个运用同一组标量的向量空间组合在一起，我们通常会将它们的向量集合做积，然后对加法和标量乘法进行定义，以确保最终得到的结果还会是一个向量空间。
然而，用这种方式并不总能得出让我们全然满意的结果。具体说来，如果想要得到乘积V×W的维度，我们要把V的维度和W的维度相加。而问题在于，如果这是一个积，我们不是应该将它们相乘吗？
张量积V⊗W的出现，就很好地解决了这个问题。张量积也是一个向量空间，但我们将这个向量空间里的向量称之为张量。将V和W的维度相乘，就可以得到V⊗W的维度。
张量积还解决了一个特殊的代数问题。简单说来，每一个符合我们要求（用术语讲是“双线性”）的从V×W到另外一个向量空间Z的映射，都可以以一种唯一的方式由V×W到V⊗W的映射和某个由V⊗W到这个向量空间的线性映射复合而成。
2.关键点梳理
取两个向量空间V和W，它们共用一组标量。它们的张量积V⊗W构成了一个新向量空间，所用的也是同一组标量。该空间内的向量包含了任意一个V中元素和W中元素构成的所有可能的元素对，外加上它们之间相加的所有方式。
举例来说，这个新空间内的向量可能会形如v1⊗w1+v2⊗w2，其中v1、v2是 V中的向量，w1、w2是W中的向量。
参考阅读//(www.chuimin.cn)
No. 7 集合论，第18页
No. 8 积，第20页
No. 57 向量，第118页
No. 76 维度，第156页
右图：张量积可以把一个不完全的线性映射（h）转化为一个线性映射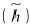
。
3.一分钟记忆
张量是某个特殊向量空间的向量，这个向量空间是由其他向量空间取张量积得到的。
通过取张量积，我们可以将向量空间乘在一起，得到一个新向量空间。
有关2页纸图解数学 : 以极聪明的方式，让你三步读懂数学的文章
- 详细阅读
-
空间直角坐标系与向量概念详细阅读
一、空间直角坐标系在空间，使3条具有相同单位长度的数轴相互垂直且相交于一点O，这3条数轴分别称为x轴、y轴和z轴，一般是把x轴和y轴放置在水平面上，z轴垂直于水平面.z轴的正向按如图7.1所示的右手法则判断，具体规定如下：伸出右手，让四指与大拇指垂直，并使四指先指向x轴的正向，然后让四指沿握拳方向旋转90°指向y轴的正向，这时大拇指所指的方向就是z轴的正向.这样就组成了右手空间直角坐标系Oxyz.......
2023-11-20
-
目标的向量空间表示模型方案介绍详细阅读
一个目标在上述约定下可以看成是n维空间中的一个向量，这就是向量空间模型的由来。下面结合目标的表示，给出其定义。，td}；2）依据目标特征项序列，对训练集和测试集中的各个目标样本进行权重赋值、规范化等处理，将其转化为机器学习算法所需的模式向量。图6-2 目标的向量空间模型示意图......
2023-06-28
-
线性子空间的生成与向量组的等价性详细阅读
，βt）.进一步有，等价的向量组生成相同的线性子空间.命例4.9 对任意一个向量组α1，α2，…，αs}.这两个命题的证明留作习题.定理4.7 若W是n维线性空间V的子空间，则对W的任意一组基α1，α2，…......
2023-11-22
-
介绍标量与向量详细阅读
6.3.3 向量的表示法6.3.4 向量大小的计算6.3.5 向量的平行、相等与相反的定义向量具有大小与方向的双重属性，因而在此描述与说明向量平行、相等与相反。......
2023-06-29
-
从存储器域到PCI总线的地址空间转换详细阅读
图2-4 MPC8548处理器存储器域到PCI域的转换在介绍MPC8548处理器如何使用Outbound寄存器组进行存储器域地址空间到PCI总线域地址空间的转换之前，本节将首先介绍Outbound寄存器组中的相应寄存器。该位是Outbound窗口的使能位，为1表示当前Outbound寄存器组描述的存储器地址空间到PCI总线地址空间的映射关系有效；为0表示无效。检查LAWBAR和LAWAR寄存器，判断当前36位的物理地址是否属于PCI总线空间。......
2023-10-20
-
支持向量机分类方法优化为：掌握支持向量机的分详细阅读
由线性判别函数的设计过程可知，对于线性可分集，总能找到使模式样本正确划分的解。d维空间中线性判别函数的一般形式为g=ωX+b，分类面方程为：ωX+b=0将判别函数进行归一化，使两类所有样本都满足|g|＞1，这样分类间隔就等于2/‖ω‖。对于线性不可分问题，可以用类似于广义线性判别函数的方法，通过事先选择好的非线性映射将输入模式向量映射到一个高维空间，在这个空间中构造最优分界超平面。......
2023-06-16
-
向量线性相关-《高等代数》详细阅读
在线性空间中，向量的加法与数乘运算统称为向量的线性运算.本节研究向量在线性运算之下的关系，也就是通常所说的向量的线性相关性.定义4.2 若α1，α2，…，s.因此表示方法是唯一的.证毕.推论4.1 零向量由一个线性无关向量组线性表示的方法是唯一的.定义4.4 设向量组A：α1，α2，…......
2023-11-22
相关推荐