至少在写本书的时候，我们还不清楚孪生质数猜想到底是真是假，但是有一个国际合作项目似乎正有着不错的进展。一些非常大的孪生质数已经被电脑找到了——2016年9月，一对孪生质数被发现。参考阅读//No. 14 自然数，第32页No. 16 希尔伯特旅馆，第36页No. 17 质数，第38页3.一分钟记忆一组孪生质数是指两个足够接近的质数。孪生质数猜想认为，我们总能无穷尽地找到一组更大的孪生质数。......
2023-11-22
猜想成功！找零点黎曼猜想揭秘
【摘要】：黎曼猜想说的是，ζ函数没有其他形式的零点，它的所有零点都在这两种形式的范畴内。参考阅读//No. 4 极限，第12页No. 9 映射，第22页No. 14 自然数，第32页No. 17 质数，第38页No. 20 负数，第44页No. 33 复数，第70页3.一分钟记忆黎曼ζ函数的零点似乎只有负偶数和形如2+xi 的复数这两种可能，但是目前我们还没有给出证明。
波恩哈德·黎曼（1826—1866）
我们已经确定，ζ函数的所有非平凡零点都处于这块临界区域内，但它们是否都在这条临界线上呢？
1.多维度看全
黎曼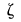
函数是一个从复数到复数的映射。其中具体的细节对我们并不是特别重要，我们只需要知道，对这个函数的计算涉及无穷项连加，而这是以极限的形式存在的。我们可以先简单地把黎曼ζ 函数看作从x到每一个自然数n所对应的
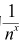相加起来的和的映射，但真正的定义要更加复杂，因为我们需要引入名为“解析延拓”的概念。
我们可能会很自然地想知道，存在哪些数可以通过ζ函数映射到0。通过解析延拓可知，所有的负偶数都能满足这一点。这些数值很明显，所以我们称它们为函数的平凡零点。
ζ函数还有许多非平凡零点，但它们都是形如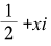
的复数。黎曼猜想说的是，ζ函数没有其他形式的零点，它的所有零点都在这两种形式的范畴内。
2.关键点梳理
我们已经通过计算机证明出，ζ函数的前1013个非平凡零点都符合黎曼猜想。哪怕只有一个例外出现，这个猜想都将被证伪。当然，这种方法只可能将该猜想证伪，无法证明该猜想为真。
ζ函数的零点分布与质数的分布之间存在某种深刻的联系。如果黎曼猜想能够得到证明，或许我们就能更好地理解质数。
参考阅读//(www.chuimin.cn)
No. 4 极限，第12页
No. 9 映射，第22页
No. 14 自然数，第32页
No. 17 质数，第38页
No. 20 负数，第44页
No. 33 复数，第70页
3.一分钟记忆
黎曼ζ函数的零点似乎只有负偶数和形如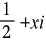
2+xi 的复数这两种可能，但是目前我们还没有给出证明。
除盛名之外，与质数之间的联系也赋予了这个问题十分重要的意义。
有关2页纸图解数学 : 以极聪明的方式，让你三步读懂数学的文章
- 详细阅读
-
哥德巴赫猜想数学图解：质数相加奇迹揭秘详细阅读
哥德巴赫在信中提出了他的猜想：所有能被写成两个质数之和的整数，都能被写成三个、四个直至更多个质数之和，直到所有的项都不能再被分解。质因数分解总是存在且具唯一性，这意味着，我们总能对一个给定的数进行质因数分解，并且每个人得到的结果都一样。与质因数分解不同，将一个偶数分为两个质数之和的方式并不总是唯一的。......
2023-11-22
-
混沌与宇宙：科学事实与猜想详细阅读
是的，我们这个宇宙是在不断变化的。因为即使在最热的恒星内部，温度也未达到足以 “烹饪”出重原子核的极高程度。对于这两个问题，最合适的答案是通过研究“宇宙膨胀”现象得出的。但是这种极为致密的状态不会长期存在，只需要两秒钟，在迅速的膨胀作用下，宇宙的密度就能达到水的几百万倍；几小时后，就会达到水的密度。......
2023-08-05
-
翻转空间：科学事实与猜想详细阅读
对于我们生活于其中的三维空间，我们也可以提出类似的问题。假如设想的隧道数目越来越多，越来越细，它们最终会在苹果内得到两个互相交错的独立空间，它们只在公共表面上相连。但是这个空间对于处于内部、不了解“外面”的人来说，就是一种具有确定大小但是没有明确边界的东西。与此同时，我们也对第二个苹果进行手术，把它缩小成樱桃那么大。第二步把被缩小的苹果放在第一个苹果所形成的两个夹口中间。......
2023-08-05
-
无穷大数的计数与比较方法，揭秘科学中的事实与详细阅读
但的确有一些无穷大的数，它们比我们可以写出的任何数都要大，不管我们花多长时间都写不出来。康托尔提出了与此相同的方法，用于比较两个无穷数。但这只是你的印象，为了得到准确的答案，你必须运用上面的方法来比较这两个无穷数。根据我们比较无穷数的规则，我们不得不承认偶数数列的无穷数和所有数字的无穷数一样大。实际上，在无穷数的世界里，部分可能与全体相等！......
2023-08-05
-
时间空间转换：科学中的事实与猜想详细阅读
尽管数学试图去证明在一个四维世界中，空间和时间的统一并不能完全消除距离和持续时间之间的差异，但它们确实揭示了这两个概念之间的相似之处，这在爱因斯坦之前的物理学中是前所未有的。事实上，现在应将各个事件之间的空间距离和时间间隔视作在空间轴和时间轴上的投影，因此四维直角坐标系的旋转可能导致部分空间距离转换为持续时间，反之亦然。空间和时间仅是亘古不变的四维坐标轴的投影，是四维空间几何学的必然结论。......
2023-08-05
-
15号科拉茨猜想：简化讲解，解决难题详细阅读
迭代的过程在科技领域，尤其是计算领域中，有着显著的重要性，但人们尚未从科拉茨提出的这个迭代过程中，挖掘出有实际应用意义的内容。科拉茨猜想之所以如此闻名，是因为还没有人找到解决它的办法。保罗·艾狄胥曾宣称，科拉茨猜想的解决是“全然无望的”。参考阅读//No. 6 哥德尔不完全性定理，第16页No. 14 自然数，第32页No. 89 迭代，第182页No. 91 混沌理论，第186页科拉茨分形是由用复数进行科拉茨游戏得到的。......
2023-11-22
-
庞加莱猜想:数学图解和简化法则详细阅读
“聚焦”于某些特殊类型的流形，我们可以得到很有用的结果。我们可以再进一步，专门关注“单连通”的流形。庞加莱猜想认为，任何一个闭的单连通三维流形都是一个三维球面。2006年，格里戈里·佩雷尔曼完成了对该猜想的证明，他还顺带证明了与之联系密切的瑟斯顿几何化猜想。随后，佩雷尔曼的结论可以很好地帮助我们对三维闭流形进行分类。......
2023-11-22
相关推荐