解读丢番图方程不可判定的整数问题

2023-11-22 理论教育版权反馈

【摘要】：和丢番图方程有关的问题有着十分悠久的历史。

上图：毕达哥拉斯和他的学派成员都认为，整数具有某种神秘的性质，并十分看重有关整数的问题。

1.多维度看全

丢番图方程是一个求整数解且系数均为整数的多项式方程。举例来讲，方程x²+6x-16=0的整数解是x=2和x=-8（请自行检验一下！）。而方程x²-2=0不存在整数解。

和丢番图方程有关的问题有着十分悠久的历史。比如，毕达哥拉斯学派就曾试图寻找方程x²+y²=z²的解——这是一个与三角形勾股定理相关的问题。你可能会知道，x=3、y=4、z=5是其中一个解。除此之外，这个方程还有无穷多个解。截至公元前350年，人们已经发现了至少三种方法可以用来找到解。

1900年，大卫·希尔伯特谈及了23个尚未解决的问题，他相信这些问题会对下个世纪的数学有着重要的意义。其中的第十个问题就是要求找出一个可以得出一个任意给定的丢番图方程是否有解的算法（用现代术语来讲，一个计算机程序）。70年后，尤里·马季亚谢维奇（Yuri Matyiasevich）采用哥德尔第一不完全性定理中所使用的一些方法，证明了这样的算法永远不会存在。

2.关键点梳理

丢番图方程之所以很难解，是因为整数构成了一个环，其中乘法运算和取幂通常不存在逆。

通过使用有理数，我们可以求解方程5x=3：将等式两边同时除以5，我们可以得到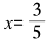，但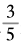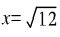并不是一个整数，所以它被舍掉了。类似地，对于方程x²=12，我们可以得到　，而这只在实数范围内成立。