三角形在三维空间内的等价物是四面体。我们可以将单纯复形看作是对它所处的空间进行三角剖分，即将其分割为最简单的部分。单纯形的要点在于它们十分简单，且单纯复形可以被分解为单纯形，因此为了更好地掌握一个空间，我们可以对它进行三角剖分，这是现代几何学与拓扑学的一个基本工具。对空间进行三角剖分，可以为我们带来一个全新的、更侧重拓扑意义的视角。......
2023-11-22
三步读懂数学，轻松掌握伽罗瓦理论
【摘要】：特别是，我们会更进一步研究由域的扩张到其自身的映射。参考阅读//No. 9 映射，第22页No. 21 有理数，第46页No. 38 群，第80页No. 42 环和域，第88页No. 59 欧几里得空间，第122页3.一分钟记忆通过给域添加一些额外的元素，我们可以对域进行扩张。伽罗瓦理论有助于我们对域的扩张进行精确探究，并从中精准地提取出我们需要的信息。
上图：多项式x5-x-1的阶数是5，但是它的图像与x轴只有一个交点。右图：这个域的自同构群和等边三角形的对称群有着相同的结构。
1.多维度看全
如果某个数字系统不包含我们需要的某个数，进入另一个有着大量我们不需要的数字的系统会使我们得不偿失。举例来讲，有理数可以帮助我们解决很多问题，但是不能用来解决方程x2-2=0，那么为什么不能单单把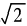
加到有理数里，让问题得以解决呢？
如果我们要保证这个数字系统仍然是一个域，我们需要让其包含这个新加入的数与任何一个有理数相加和相乘的所有方式，得到的结果被称为域的扩张。这种观点可以使某个特定的问题成为我们关注的焦点。
特别是，我们会更进一步研究由域的扩张到其自身的映射。这些映射只是改变了新加进来的事物的排列顺序，而其他的都保持不变。这些域扩张的自同构形成了一个群——伽罗瓦群，它的结构涵盖了扩张本身的相关信息。
2.关键点梳理
伽罗瓦理论是我们将对称（即群论）应用到域扩张时所产生出来的一种非常通用的方法。其具体细节有些琐碎，但是最终的结果十分引人注目。
举例来讲，基础的伽罗瓦理论证明了两个经典问题——用尺规作图进行倍立方和仅用欧几里得方法三等分角——的不可解。而在这之前，许多善于思考的伟人都为这些问题投入了大量的时间和努力。
参考阅读//(www.chuimin.cn)
No. 9 映射，第22页
No. 21 有理数，第46页
No. 38 群，第80页
No. 42 环和域，第88页
No. 59 欧几里得空间，第122页
3.一分钟记忆
通过给域添加一些额外的元素，我们可以对域进行扩张。每一个域扩张都和初始的域通过其伽罗瓦群联系起来。
伽罗瓦理论有助于我们对域的扩张进行精确探究，并从中精准地提取出我们需要的信息。
有关2页纸图解数学 : 以极聪明的方式，让你三步读懂数学的文章
- 详细阅读
-
2页纸图解数学：轻松读懂数学的三步法详细阅读
19世纪90年代，大卫·希尔伯特证明出一个结果，它被称为“零点定理”，这个定理用精准的术语对这一对应关系做了探讨。这就是零点定理的核心，也是代数几何成立的条件。和代数拓扑类似，代数几何的核心在于，我们已经对环的性质有了许多了解，所以把簇“翻译”成环的语言处理，要比直接处理更方便。零点定理为代数几何的建立提供了基本词典。......
2023-11-22
-
2页纸图解数学：以迭代重复的力量，轻松三步读详细阅读
靠近那个点的元素——我们这时引入一个度量标准——可以被这一点吸引或排斥，与之对应地，我们称这一点为汇点或源点。在这个迭代里，0是不动点，且是汇点，因为它把附近的数字都“吸引”过去了。参考阅读//No. 7 集合论，第18页No. 9 映射，第22页No. 15 科拉茨猜想，第34页No. 74 度量空间，第152页No. 90 布劳威尔不动点定理，第184页No. 91 混沌理论，第186页右图：许多工业生产过程都会将同一个步骤不断进行迭代。......
2023-11-22
-
最强数学图解书，让你轻松读懂数学详细阅读
接下来，试着厘清其可能导致的结果，或许就会发现矛盾。此外，如果一个命题为真，那么它所有的蕴涵命题均为真。参考阅读//No. 5 逻辑，第14页No. 14 自然数，第32页No. 27 康托尔对角线论证，第58页No. 54 病态函数，第112页No. 69 不可能的构造，第142页布尔代数的部分内容：如果一组命题为真，那么指向它的一组子命题不可能为假。如果一个命题为真，那么它所有的逻辑结果也同样为真。......
2023-11-22
-
三步读懂数学，极聪明方式！详细阅读
几个世纪以来，亚里士多德的研究成果在基督教世界和伊斯兰世界一直是学术界的黄金准则。亚里士多德首先制定了一系列法则，对逻辑有效性进行了详细的规定。对于一个论证而言，真实性取决于内容本身，是否对确则与逻辑形式有关。......
2023-11-22
-
2页纸图解数学：极简三步读懂数学详细阅读
对于空间内其他任意一点，我们从原点向它做一条直线，并在末尾处画上一个指向该点的箭头，这样一来，我们便得到了一个向量。在三维空间内，我们以自身所处的位置作为原点，用“上”“左”“前”来表示方向。......
2023-11-22
-
读懂汽车电路图，轻松掌握电控悬架系统详细阅读
以奥迪A6轿车电控悬架系统为例，介绍电控悬架系统电路图的识读方法。测量前、后桥减振支柱的压力或蓄压器内的压力，压力传感器G291采用的是电容测量原理。供电电压由空气悬架控制单元来提供，车身加速度当前的电压值可通过测量数据块读出。图5-20 奥迪A6空气悬架系统电路图5-20 奥迪A6空气悬架系统电路（续）......
2023-08-29
-
轻松掌握极聪明的数学技巧详细阅读
许多过程都可以用极限来模拟，放射性衰变就是其中一例。极限就为表述这种最终状态，尤其是越来越接近某个值，却从未到达这个值的无穷过程的最终状态提供了一种方式。参考阅读//No. 26 实数，第56页No. 53 微积分基本定理，第110页3.一分钟记忆有些无穷过程属于那种逐渐趋近某种状态，而永远不会达到那种状态的情况。一个有极限值存在的过程会越来越接近它的极限值。......
2023-11-22
相关推荐