2页纸图解数学:极聪明的三步读懂数学

2025-09-30 理论教育版权反馈

【摘要】：事实上，康托尔找到了一个可以构造出许多不同大小的无穷的方法，正好解决了我们的问题。而有了一般性的对角线论证后，我们可以证明，这一点对于无穷集合同样成立。通过不断对一个无穷集取幂集，我们可以得到一个更大无穷集的无穷序列：无穷基数。

上图：一个集合的幂集总是比原集合包含更多的元素，即便原集合也是无穷集。

1.多维度看全

康托尔对角线论证向我们展现了两种无穷，其中一个比另一个大。我们自然会问，是否有着更多更大的无穷，它们又是怎样构造出来的。事实上，康托尔找到了一个可以构造出许多不同大小的无穷的方法，正好解决了我们的问题。

如果S是一个集合，我们可以考虑它的所有子集。这些子集构成的集合叫作集合S的幂集，写作2^S。我们可以把S想作商店里在售的所有商品，把2^S想作你逛完商店后购物筐里商品构成的所有可能的集合。

幂集2^S一定总是会比集合S大。在S为有限集时，这一点很好证明。而有了一般性的对角线论证后，我们可以证明，这一点对于无穷集合同样成立。因此，只要对无穷集不断取幂集，我们就可以不断构造出更大的无穷集。

2.关键点梳理

康托尔将由所有自然数构成的无穷集的大小写作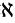₀。现在，考虑自然数集的所有子集：其中一个包含所有偶数，其中一个包含所有质数，其中一个包含所有比7大的数，等等。所有这些子集在一起构成了集合，我们将它的大小写作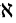₁。

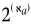从施罗德-伯恩斯坦定理的意义上来讲，一个集合的幂集总会比原来的集合要大，这意味着，如果a是一个无穷集，那么它的幂集就要比它大一些。

参考阅读//

No. 7集合论，第18页(https://www.chuimin.cn)

No. 12 施罗德-伯恩斯坦定理，第28页

No. 14 自然数，第32页

No. 17 质数，第38页

No. 27 康托尔对角线论证，第58页

No. 29 连续统假设，第62页

右图：前五个英文字母构成的集合的幂集包含了前者所有的子集。

3.一分钟记忆

一个集合的幂集是这个集合的所有子集构成的集合，它所包含的元素数量总会比原先的集合要多。

通过不断对一个无穷集取幂集，我们可以得到一个更大无穷集的无穷序列：无穷基数。