在初中我们学习了正整数指数,我们知道a2=a·aa3=a·a·aan=a·a·…......
2023-11-22
1.多维度看全
用边长乘以边长可以得到正方形的面积,如果L是边长,那么L2就是面积。用这个方法,先用边长乘以边长求出一个面的面积,再乘以一次边长,就可以求出立方体的体积,写成L3。上述这些不断乘以同一个值的过程是幂最基础的形式,并且有着一定的历史渊源。
尽管幂的这一现代符号是经过很长时间逐步发展出来的,它却掩盖了这一概念的统一性和广度。幂可以拓展为负数幂和分数幂,甚至是其他数字系统里的数,从而得出许多实用而优美的结论。和积类似,升次到一个幂(也叫作取幂),甚至可以推广至许多数字以外的数学对象。
2.关键点梳理
设A为任意数。如果n是一个自然数,An就表示A乘以自身n次。我们可以证明An×Am=A(m+n) ,这需要我们先规定好:A1=A和A0=1。这两条是确保An×Am=Am+n对于所有的n和m都成立的常规条件。
现在,假设A2×Am=A0 ,为保证前后一致,只能有m=-2。基础代数告诉我们,Am应是1/A2,因此我们将负数幂看作“正数幂分之一”。
自然数幂还有一个公式:(An )m=Am×n。现在,假设(A2 )m=A1——我们将A平方之后再取平方根便会产生这个结果。然而,2×m=1意味着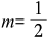 ,因此分数幂意味着取根。
,因此分数幂意味着取根。
参考阅读//
No. 8 积,第20页
No. 14 自然数,第32页
No. 20 负数,第44页(www.chuimin.cn)
No. 21 有理数,第46页
No. 25 无理数,第54页
No. 30 超越数,第64页
右图:自然数幂与面积、体积以及更高维计算相关。
3.一分钟记忆
将一个数升次到一个自然数幂,我们要将它重复地乘以自身,而其他类型的幂遵循着下面的基本原则:
X n:将X乘以它自身n次
X -n: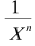
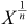 :取X的n次方根
:取X的n次方根
有关2页纸图解数学 : 以极聪明的方式,让你三步读懂数学的文章

想要解决刚刚的问题,我们只需要以2为底取对数,得到的结果约为6.644。这意味着,再过6分38秒多一点的时间,细菌的数量就会超过100。事实证明,自然过程和数学过程一样,通常会遵循对数式的增长。将n取以A为底的对数,写作logA,这个数代表了你要将A乘以自身几次后能得到B。参考阅读//No. 22 幂,第48页No. 25 无理数,第54页No. 45 费马最后定理,第94页3.一分钟记忆对数用来解形如An=B的方程,其中n为未知量。......
2023-11-22

4.风切换指数推荐使用幂定律拟合风切变幂律公式和风切变指数的计算,风切变幂律公式为式中 α——风切变指数;v2——高度z2处的风速,m/s;v1——高度z1处的风速,m/s。......
2023-06-23

设z1 =r1eiθ1,z2 =r2eiθ2,··· ,zn =rneiθn是n个非零复数,用数学归纳法可以得到这n个复数的乘积为特别地,当这n个复数相同时,我们把n个相同的复数z的乘积称为z的n次幂,记作zn.设z =reiθ,则zn =rneinθ =rn(cos nθ+i sin nθ).当r =1时,即z =cos θ+i sin θ,有(cos θ+i sin θ)n =cos nθ+i......
2023-10-30

图3-31 基于最小二乘的基窗F卷积窗C及滤波器特性实现上述结果的MATLAB代码如下:图3-31 基于最小二乘的基窗F卷积窗C及滤波器特性实现上述结果的MATLAB代码如下:卷积窗C性能参数B=0.2165,A=-14dB,D=-10.15dB。对比图3-16七种基窗可看出,利用最小二乘得到的基窗综合性能最好。此外,基于此结果基窗F的滤波器具有最小的均方误差。......
2023-06-23

聚类系数节点i的邻居节点之间有可能互为邻居,这被称为网络的聚类特性。复杂网络的这种幂律分布特点成了它的致命弱点。研究表明,规则网络具有大的聚类系数和大的平均距离,随机网络具有小的聚类系数和小的平均距离。图3-4无标度网络......
2023-07-02

群幂是一个专门为社群主打造的专业化社群管理平台,其口号为“让志同道合者相遇在群幂”。在激活社群活力方面,群幂在其社群管理平台主要开展了以下工作:话题讨论,平台特有活动功能,相对微信群的优势在于:即时场景话题的交流空间,群成员凭自愿参加,同时话题结束后内容会独立保存,并与直播活动成员一样可以进行打赏。......
2023-10-31

图4-18三多神图片来源:木府提供需要特别一提的是历来被纳西族视为保护神的“三多”及其崇拜。“三多”的全称是“阿普三多”;“阿普”为纳西语祖宗之称,“三多”是神名。“三多”由此成为纳西人供奉的战神。因此,到目前为止,东巴信仰也只能算作是人类早期文明的一种信仰模式。这种兼收并蓄、多种宗教并存的局面,使得以丽江为中心的纳西族文化也呈现出一种灿烂多元的色彩。......
2023-09-18
相关推荐