1949年以来到改革开放前，我国污水处理的需求主要来自工业和国防。1990年以来，全球污水处理表观消费量以年均6%的速度增长。而1990—2000年期间，我国污水处理表观消费量年均增长率达到17.73%，是世界年均增长率的2.9倍。但中国的污水处理率与发达国家相比，还存在着明显的差距，且处理设施的负荷率低。......
2023-11-21
大型地下污水处理厂构筑物设计与施工：上海白龙港提标工程
【摘要】：以上就是王铁梦教授提出的超长混凝土结构裂缝控制中“抗放兼施”的基本概念和理论基础。连续超长筏板的受力机理与其相同。
4.2.3.1 定义和原理
跳仓法是指先将超长混凝土结构分为若干小块体间隔施工，经过短期的应力释放再将其连成整体，依靠混凝土抗拉强度抵抗剩余温度收缩应力的施工方法。在分仓间歇阶段，结构的温度收缩应力得以显著地松弛和释放，从而确保在最终封仓后，混凝土结构承受的温度收缩应力不超过其抗拉能力。
对于如图4－4所示的两端固定约束的梁，若将其中一端的约束全部释放，在各种收缩变形影响下，梁体会发生如下变形：
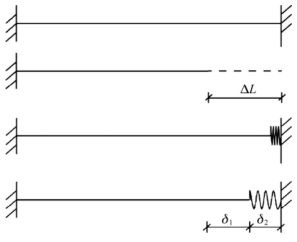
图4－4 超长混凝土跳仓法受力机理及应力计算示意
设想在自由端施加一个外力P，将杆的自由端拉回到原来收缩前的位置，则梁内的应力为
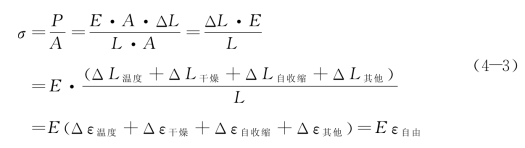
若将外力P 换作一个弹性约束，则梁的收缩会使弹簧产生δ2的变形，此为梁的实际变形。同时，弹簧又会对梁的收缩产生一个反作用力，使得梁在收缩变形ΔL 的基础上，发生反向伸长变形δ1。显然，δ1+δ2=L。此时，梁的应力为
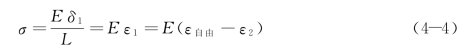
根据以上分析可知在不同的约束条件下，梁的应力为
可见，在收缩变形ΔL 的作用下，实际变形δ2其实是释放掉的部分，约束变形δ1则为构件需要抵抗的部分。
根据上述理论分析可制定出跳仓法的基本原则：
（1）通过改良材料配合比等措施减少整体收缩变形ΔL；
（2）采用分仓间隔施工的方法，让各个仓块尽可能释放早期剧烈的收缩变形，即增大δ2；
（3）通过确保良好养护、改良配筋等措施，增加混凝土结构的抗拉能力，从而确保其能承受剩余的约束变形δ1。
以上就是王铁梦教授提出的超长混凝土结构裂缝控制中“抗放兼施”的基本概念和理论基础。
4.2.3.2 最小跳仓长度
在跳仓法施工方案的设计中，需要对跳仓和合龙阶段的温度应力和裂缝间距进行验算。这里以连续长墙为例，分析超长混凝土在温度收缩作用下的应力分布，以及结构长度和刚度对温度收缩应力的影响。连续超长筏板的受力机理与其相同。
如图4－5所示的长L、高H、厚t 的连续长墙在温度作用下将产生温度应力。根据工程实践可知，温度应力随L 的增大而增大。当L 增大到某个临界值时，温度应力将超过混凝土的抗拉极限，引起混凝土开裂。因此，在跳仓法施工方案的设计中，应计算出L 的临界值［L］min（称为最小跳仓长度），并保证跳仓块的长度小于该临界值。为解决这一问题，王铁梦教授在1974年通过分析温度应力产生的实质，引入了约束位移和自由位移的概念，现简单推导如下。
图4－5 连续长墙温度收缩应力计算图示
当长墙相对地基有一温差ΔT 时，在长墙的任一点x 处截取dx 的微段。假定在离地基高度为H 的范围内，墙体均匀受力。其中，墙体截面的正应力为σx，合力为N；地基对墙底的剪应力为τ，合力为Q。根据x 方向上的平衡方程可得
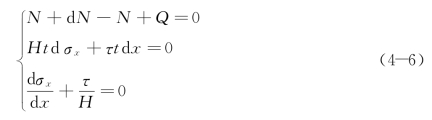
墙体截面上任意点的位移由约束和自由两部分组成：
根据式（4－7），可得位移的一阶和二阶导数为
根据弹性力学的基本知识可知正应力与位移之间的关系为(www.chuimin.cn)
对σx求一阶导数，同时将式（4－9）代入，可得
剪应力和位移之间的关系为
式中，Cx为水平约束系数。将式（4－11）和式（4－12）带入式（4－6）中的第三个方程，可得
令β=
，则上式可改写为
此微分方程的通解为
根据图4－5可得边界条件为
将边界条件带入式（4－15），可得偏微分方程的特解为
由位移解可进一步得到正应力和剪应力为
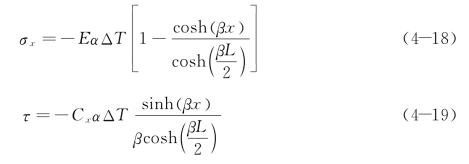
式（4－18）和式（4－19）即连续超长结构在温度收缩作用下的应力分布。从工程实践角度，正应力σx为结构设计中的控制应力之一，是经常引起垂直裂缝的主要原因。其最大值在x=0处（由于对称关系，此时基地对墙体底面的剪应力为零）：
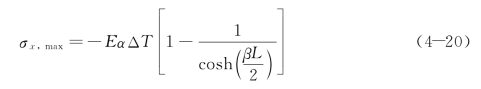
跳仓法施工过程中的超长混凝土温度收缩应力也可采用式（4－20）进行计算，只需在分仓浇筑和合龙阶段分别采用分仓块和整体结构的尺寸即可。此外，将混凝土的极限拉伸应变带入式（4－20），可得：
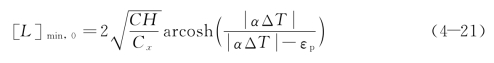
此时，若进一步增加墙体的长度，式（4－20）中的σx，max会超过混凝土的抗拉强度，墙体将会在x=0 处出现裂缝。因此，最小裂缝间距（最小跳仓长度）应为式（4－21）中［L］min，0的一半，即
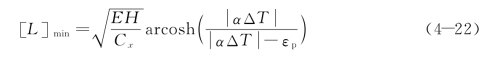
式中 α——线膨胀系数；
H——均拉层厚度，指能够假定截面上应力均匀分布的最大高度；
Cx——水平约束系数；
εp——混凝土的极限拉伸应变，一般情况下为（1.0～2.0）×10－4；
E——混凝土弹性模量；
ΔT——温差。
式（4－22）既可用于推导裂缝间距，也可用于验算跳仓块和最终合龙长度是否满足抗裂条件。ΔT 中可以叠加考虑昼夜及季节温差，在实际工程设计中应用十分方便。值得注意的是，如果计算结果为正无穷，则说明混凝土材料还能承受的拉伸应变值大于温度收缩值，所以即便是处于完全约束状态，混凝土理论上也不会因为收缩而开裂。而混凝土结构的长度只决定约束的大小，因此，此时理论上无论混凝土结构有多长，都不会发生开裂。
有关大型地下污水处理厂构筑物设计与施工 上海白龙港污水处理厂提标工程的文章
- 详细阅读
-
大型地下污水处理厂施工案例：上海白龙港污水处详细阅读
表3－3本工程基坑围护施工概况3.4.2.2钻孔灌注桩施工双排桩支护体系采用钻孔灌注桩的形式，其施工流程如图3－22和图3－23所示。基点应做特殊专门保护，不得损坏。钢筋笼安装完毕后应进行隐蔽工程验收，合格后应立即浇筑水下混凝土。......
2023-11-21
- 详细阅读
-
深基坑设计：上海白龙港污水处理厂提标工程详细阅读
由此形成大范围放坡与双排桩结合的基坑围护方案。同时在第一级坡外侧5m 处设置16m 长3φ850＠1200三轴搅拌桩止水帷幕，保证边坡水位在基坑开挖阶段低于放坡底部。图3－15开挖深度12.8m 的基坑剖面图3－16开挖深度14.5m 的基坑剖面3.3.2.2双排桩结构设计图3－17开挖深度15.8m 的基坑典型剖面本基坑开挖深度存在12.8m、14.5m 及15.8m 三种。......
2023-11-21
-
上海白龙港污水处理厂提标工程施工流程及部署详细阅读
图5－20预制节点施工流程图5－21预制板施工流程5.3.1.4施工部署本工程施工现场在场地西侧开设施工车辆通行大门（1号门）。......
2023-11-21
-
上海白龙港污水处理厂提标工程成功完成详细阅读
1.3.1.3污水厂现状上海市白龙港污水处理厂经过升级改造工程、扩建工程、扩建二期工程、污泥处理处置工程、污泥应急工程等建设，已基本形成了四大区域，如图1－12 所示。......
2023-11-21
-
上海白龙港污水处理厂提标工程改造方法详细阅读
表4－3跳仓法中水泥的选用注：所用水泥在预拌混凝土搅拌站的入水泥储仓温度不宜大于60℃。因此，跳仓法施工的混凝土可掺加部分粉煤灰，并辅以少量矿粉。......
2023-11-21
-
上海白龙港污水处理厂提标工程成果详细阅读
为了进一步提升上海白龙港污水处理厂的污水处理能力，对该厂实施了提标工程，设计规模280万m3／d，采用减量达标的方式。本书主要介绍上海白龙港污水处理厂提标工程西北地块全地下污水处理厂的设计、施工及建设管理情况。......
2023-11-21
相关推荐