，λn，由于A，B都是实对称矩阵，所以存在可逆矩阵P1和P2，使得于是有P1-1AP1=P2-1BP2，即A=B，或-1A=B.由于P1P2-1是可逆矩阵，所以A～B.......
2023-10-27
实对称矩阵的合同及相似判定
【摘要】：（1）同阶实对称矩阵A，B合同的判定.①用定义法：A，B合同存在可逆矩阵C，使得CTAC＝B.②用正、负惯性指数：A，B合同pA＝pB，qA＝qB.（相同的正、负惯性指数）③用传递性：A合同于C，C合同于B，则A合同于B.【注】同阶矩阵A，B相似的判定.（1）用定义法：A，B相似存在可逆矩阵C，使得C－1AC＝B.（2）用传递性：A相似于C，C相似于B，则A相似于B.（常考C为Λ 的情形）（3）用
（1）同阶实对称矩阵A，B合同的判定.
①用定义法：A，B合同⇔存在可逆矩阵C，使得CTAC＝B.
②用正、负惯性指数：A，B合同⇔pA＝pB，qA＝qB.（相同的正、负惯性指数）
③用传递性：A合同于C，C合同于B，则A合同于B.
【注】同阶矩阵A，B相似的判定.
（1）用定义法：A，B相似⇔存在可逆矩阵C，使得C－1AC＝B.
（2）用传递性：A相似于C，C相似于B，则A相似于B.（常考C为Λ 的情形）
（3）用结论：①同阶实对称矩阵A，B相似必合同；
②若A，B相似，则a.r（A）＝r（B），b.|A|＝|B|，c.tr（A）＝tr（B），d.A，B有相同的特征值.这四条只要有一个不满足，则A，B不相似.
见例9.12至例9.14.
（2）已知A，Λ（Λ 是对角矩阵），求可逆矩阵C，使得CTAC＝Λ.见例9.15，例9.16.
（3）已知A，B（B不是对角矩阵），求可逆矩阵C，使得CTAC＝B.见例9.17.
例9.12 设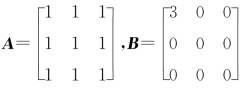
，则A与B（）.
（A）合同且相似 （B）合同，但不相似
（C）不合同，但相似 （D）既不合同，也不相似
【解】应选（A）.
因为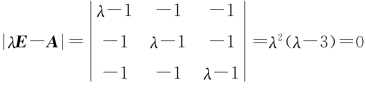
，故A 的特征值为λ1＝3，λ2＝λ3＝0，A 为实对称矩阵，必可相似对角化，于是
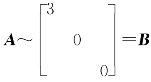，同阶实对称矩阵相似必合同，故A，B亦合同.
例9.13 设矩阵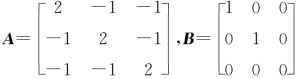
，则A与B（）.
（A）合同且相似 （B）合同，但不相似
（C）不合同，但相似 （D）既不合同，也不相似
【解】应选（B）.
因为 
所以矩阵A的特征值为3，3，0.由此可知矩阵A与B 不相似，从而选项（A）和（C）错误.
又因为实对称矩阵A相似且合同于对角矩阵
而矩阵C显然合同于矩阵B，根据合同关系的传递性知矩阵A合同于B，即选项（B）正确.
例9.14 设A为3阶实对称矩阵，互换A的1，2行得到矩阵B，再互换B的1，2列得到矩阵C，则矩阵A与矩阵C（）.
（A）合同但不相似 （B）相似但不合同
（C）合同且相似 （D）不合同也不相似(www.chuimin.cn)
【解】应选（C）.
由题设互换A的1，2行得到矩阵B，则有PA＝B，其中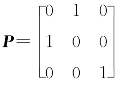
.再互换B 的1，2列得到矩阵C，则有BP＝C，从而PAP＝C.由于初等矩阵
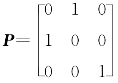满足PT＝P，P－1＝P，所以P－1AP＝C，PTAP＝C，即矩阵A与矩阵C 合同且相似，故正确选项为（C）.
【注】这是综合题，考核点为矩阵初等变换与初等矩阵的关系，初等矩阵的逆矩阵，矩阵合同与相似的概念.
例9.15 设二次型
f（x1，x2，x3）＝λ1x21＋λ2x22＋λ3x23，g（y1，y2，y3）＝λ3y21＋λ1y22＋λ2y23.
（1）证明f与g 合同；
（2）求可逆矩阵C，使在x＝Cy下，f化为g.
（1）【证】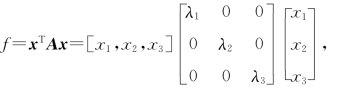 
于是f，g的二次型矩阵分别为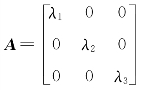
与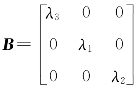
，故A，B 有相同的正、负惯性指数，A，B合同，f与g 合同.
（2）【解】令x1＝y2，x2＝y3，x3＝y1，即
则f＝g，取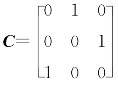
，即可在x＝Cy下，将f化为g.
例9.16 已知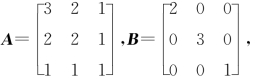 
证明A与B 合同，并求出可逆矩阵C，使得CTAC＝B.
【注】（*）处用的是先配x3，再配x2，最后配x1 的顺序，只要一次配齐一个xi，i＝1，2，3，先配谁，后配谁，是没有限制的，以利于解题为原则即可.
例9.17 已知实矩阵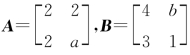
，a为正整数.若存在可逆矩阵C，使得CTAC＝B.
（1）求a，b的值；
（2）求矩阵C.
【解】（1）因AT＝A，故
BT＝（CTAC）T＝CTATC＝CTAC＝B，
所以B为对称矩阵，b＝3.
对于
对于
由于A与B 合同，记pA，qA，pB，qB 分别为二次型f，g 的正、负惯性指数，故pA＝pB，qA＝qB，于是a－2＜0，即a＜2，又a为正整数，故a＝1.
综上所述，a＝1，b＝3.
（2）由（1）得f（x1，x2）＝2（x1＋x2）2－x22，
使得CTAC＝B.
有关张宇线性代数9讲的文章
- 详细阅读
-
线性代数9讲-实对称矩阵与正交矩阵详细阅读
（1）若A为实对称矩阵，则①特征值均为实数，特征向量均为实向量.②不同特征值对应的特征向量正交.（即λ1≠λ2ξ1⊥ξ2（ξ1，ξ2）＝0，建方程）③可用正交矩阵相似对角化.（即存在正交矩阵P，使P－1AP＝PTAP＝Λ）见例8.12至例8.15.（2）若A为正交矩阵，则ATA＝EA－1＝ATA由规范正交基组成AT是正交矩阵A－1是正交矩阵A*是正交矩阵－A是正交矩阵.（3）若A，B为同阶正交矩阵......
2023-11-21
-
矩阵相似定义及性质概述详细阅读
1.矩阵相似的定义设A，B都是n阶矩阵.如果存在n阶可逆矩阵P，使得B=P-1AP，则称矩阵A与B相似，也称A与B为相似矩阵，记为A～B.2.矩阵相似的性质设A，B，C都是n阶矩阵，则有以下性质：A～A.如果A～B，则B～A.如果A～B，B～C，则A～C.如果A～B，则AT～BT，Am～Bm，λA～λB，φ～φ（其中，φ（λ）=a0+a1λ+…......
2023-10-27
-
矩阵相似对角化条件及意义详细阅读
【主要内容】1.矩阵可相似对角化的定义设A是n阶矩阵，如果它与n阶对角矩阵Λ相似，则称A可化为相似的对角矩阵，简称A可相似对角化.n阶矩阵A可相似对角化的条件：（1）A有n个互异的特征值是A可相似对角化的充分而非必要条件.（2）A是实对称矩阵是A可相似对角化的充分而非必要条件.（3）A有n个线性无关的特征向量是A可相似对角化的充分必要条件.（4）A的每个ni重特征值λi的特征矩阵λiEn-A都满足......
2023-10-27
-
该购销合同的有效性判定及合同法规详细阅读
（十一）该购销合同为何有效——谈合同及其有效性判定A服装公司产品积压，为周转资金，号召职工销售，并按销售额的百分比发给奖金，于是职工们各找销售渠道。合同成立即具有法律效力，合同因履行完毕、变更或解除而终止。合同终止即失去法律效力。本案中，C商场乙某的行为虽未经商场领导授权，但所签合同有效，C商场领导通知银行拒付资金的行为是不对的。......
2023-12-05
- 详细阅读
- 详细阅读
-
相似性替换矩阵在多序列比对算法中的应用详细阅读
等价矩阵仅考虑序列元素是否匹配。等价矩阵具有极大的局限性，因此，在实际应用中常常使用相似性替换矩阵。图4-1BLAST矩阵蛋白质的替换矩阵在设计时比DNA的替换矩阵所需考虑的因素更多，包括理化性质、替换率、亲疏水性、带电性等因素。目前PAM矩阵在蛋白质序列比对中得到了广泛应用，基础的PAM-1矩阵反映了进化中每一百个氨基酸平均发生一次突变的概率。图4-2BLOSUM矩阵和PAM矩阵的选择标准遗传密码矩阵。......
2023-10-25
相关推荐