【摘要】:(1)若A为实对称矩阵,则①特征值均为实数,特征向量均为实向量.②不同特征值对应的特征向量正交.(即λ1≠λ2ξ1⊥ξ2(ξ1,ξ2)=0,建方程)③可用正交矩阵相似对角化.(即存在正交矩阵P,使P-1AP=PTAP=Λ)见例8.12至例8.15.(2)若A为正交矩阵,则ATA=EA-1=ATA由规范正交基组成AT是正交矩阵A-1是正交矩阵A*是正交矩阵-A是正交矩阵.(3)若A,B为同阶正交矩阵
(1)若A为实对称矩阵,则
①特征值均为实数,特征向量均为实向量.
②不同特征值对应的特征向量正交.
(即λ1≠λ2⇒ξ1⊥ξ2⇒(ξ1,ξ2)=0,建方程)
③可用正交矩阵相似对角化.
(即存在正交矩阵P,使P-1AP=PTAP=Λ)
见例8.12至例8.15.
(2)若A为正交矩阵,则
ATA=E⇔A-1=AT
⇔A由规范正交基组成
⇔AT是正交矩阵
⇔A-1是正交矩阵
⇔A*是正交矩阵
⇔-A是正交矩阵.
(3)若A,B为同阶正交矩阵,则AB为正交矩阵.(A+B不一定)
见例8.16.
例8.12 设A是3阶实对称矩阵,满足 ,则关于A的秩必有().
,则关于A的秩必有().
(A)r(A)=0 (B)r(A)=1 (C)r(A)=2 (D)r(A)=3
【解】应选(A).
设λ是A 的任一特征值,则,解得λ=0或λ=-1±i,其中i是虚数单位.因为A 是实对称矩阵,其特征值λ 为实数,所以只能有λ0=0(三重),并且A 相似于对角矩阵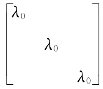 ,故r(A)=0.应选(A).
,故r(A)=0.应选(A).
例8.13 设A为3阶实对称矩阵,A的秩为2,且
(1)求A的全部特征值与特征向量;
(2)求矩阵A.
【解】(1)由于3阶实对称矩阵A的秩为2,所以0是A的一个特征值.
由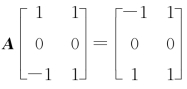 可得
可得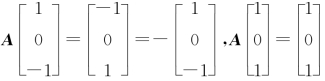 ,所以-1是A 的一个特征值,其对应的全部特征向量为
,所以-1是A 的一个特征值,其对应的全部特征向量为 (k1 为任意非零常数);1也是A 的一个特征值,其对应的全部特征向量为
(k1 为任意非零常数);1也是A 的一个特征值,其对应的全部特征向量为 (k2 为任意非零常数).
(k2 为任意非零常数).
设A的对应于特征值0的特征向量为[x1,x2,x3]T,由实对称矩阵对应于不同特征值的特征向量是正交的,知
即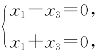 解得
解得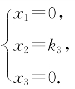
于是A的对应于特征值0的全部特征向量为 (k3 为任意非零常数).
(k3 为任意非零常数).
(2)令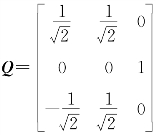 ,则Q-1AQ=QTAQ=
,则Q-1AQ=QTAQ=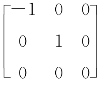 ,故
,故
【注】也可令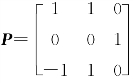 ,则
,则
例8.14 设3阶实对称矩阵A的特征值λ1=1,λ2=2,λ3=-2,且α1=[1,-1,1]T是A的属于λ1的一个特征向量.记B=A5-4A3+E,其中E 为3阶单位矩阵.
(1)验证α1 是矩阵B的特征向量,并求B的全部特征值与特征向量;
(2)求矩阵B.
【解】(1)由Aα1=λ1α1,第7讲“二(3)”的“②”,知
Bα1=(A5-4A3+E)α1=(λ51-4λ31+1)α1=-2α1,
故α1 是B的属于特征值-2的特征向量.
因A的特征值分别为λ1,λ2,λ3,故B=A5-4A3+E 的特征值分别为λ5i-4λ3i+1(i=1,2,3),即
15-4×13+1=-2,25-4×23+1=1,(-2)5-4(-2)3+1=1.
故B的属于特征值-2的全部特征向量为k1α1(k1 为任意非零常数).
因A是实对称矩阵,故B也是实对称矩阵,B的不同特征值对应的特征向量正交.设[x1,x2,x3]T是B的属于特征值1的特征向量,则[x1,x2,x3]α1=0,即
x1-x2+x3=0,
解得其基础解系α2=[1,1,0]T,α3=[-1,0,1]T,故矩阵B的属于特征值1的全部特征向量为k2α2+k3α3,其中k2,k3 为不全为零的任意常数.
(2)将B的特征向量α1,α2,α3 正交化、单位化后构成正交矩阵Q.令
【注】(1)在第(1)问中求矩阵B的属于特征值1的特征向量α2,α3 时,可以直接取成二者正交,这样第(2)问的解析中就能回避下面的施密特正交化步骤.由x1-x2+x3=0,取α2=[1,1,0]T,此时再设α3=[x1,x2,x3]T,且令αT2α3=0,得x1+x2=0,联立 可取α3=[-1,1,2]T.
可取α3=[-1,1,2]T.
(2)第(2)问也可以直接利用相似对角化求矩阵B.
例8.15 设α,β是3维单位正交列向量组,A=αβT+βαT.
(1)证明A可相似对角化;
(2)若 ,求正交矩阵C,使得CT(A+A*)C为对角矩阵,并求此对角矩阵.
,求正交矩阵C,使得CT(A+A*)C为对角矩阵,并求此对角矩阵.
(1)【证】AT=(αβT+βαT)T=βαT+αβT=A,A为实对称矩阵,必可相似对角化.
(2)【解】因为α,β是单位正交列向量组,故
①+②得A(α+β)=1(α+β),①-②得A(α-β)=(-1)(α-β).
又α与β正交,α与β线性无关,α+β≠0,α-β≠0,于是1,-1是A的两个特征值,且α+β,α-β分别为对应的特征向量.
又r(A)≤r(αβT)+r(βαT)≤r(α)+r(β)=2⇒Ax=0必有非零解.设γ是齐次线性方程组Ax=0的一个非零解,即有Aγ=0γ,于是0是A的一个特征值,γ是其对应的特征向量.
设γ=[x1,x2,x3]T,由(γ,α+β)=0,(γ,α-β)=0,其中
解得γ=[-1,0,1]T.单位化,有
记C=[η1,η2,η3],则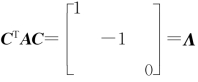 ,故
,故
故CT(A+A*)C=Λ+Λ*=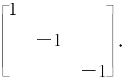
例8.16 已知n阶实矩阵A,B均为正交矩阵,则以下结论不正确的是().
(A)ATB是正交矩阵 (B)AB-1是正交矩阵
(C)-A*B是正交矩阵 (D)A-1+B是正交矩阵
【解】应选(D).
若A是正交矩阵,则ATA=E,A-1=AT.于是
①(A-1)-1=(AT)-1=(A-1)T,得(A-1)TA-1=E,即A-1为正交矩阵.以上过程可逆,故有A 是正交矩阵⇔A-1是正交矩阵.
②(ATA)*=E*=E,又(ATA)*=A*(AT)*=A*(A*)T=E,即A*是正交矩阵;
反过来说,当A*是正交矩阵时,|A*|=1或-1,又|A*|=|A|n-1=1或-1,故|A|=1或-1,且(A*)TA*=E,两边再取伴随,[(A*)TA*]*=(A*)*[(A*)T]*=|A|n-2A|AT|n-2AT=|A|2n-4AAT=AAT=E,于是A是正交矩阵.
综上,A是正交矩阵⇔A*是正交矩阵.
③(ATA)T=ET=E,即(AT)(AT)T=E,AT为正交矩阵.以上过程可逆,故有A 是正交矩阵⇔AT是正交矩阵.
④(-A)T(-A)=E,故-A为正交矩阵.A是正交矩阵⇔-A是正交矩阵.
⑤当A,B 均为正交矩阵时,ATA=E,BTB=E,于是(AB)TAB=BTATAB=BTB=E,得AB 是正交矩阵.
到此,按照以上①至⑤所述,ATB,AB-1,-A*B均为正交矩阵.
⑥当A,B均为正交矩阵时,若取B=-A-1,则A-1+B=A-1-A-1=O,不是正交矩阵.故A-1+B 不一定是正交矩阵,选(D).
8.1 设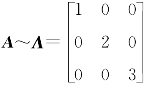 ,f(x)=x3-6x2+11x-5,则f(A)=________.
,f(x)=x3-6x2+11x-5,则f(A)=________.
8.2 设α=[1,2,3,4]T,β=[3,-2,-1,1]T,A=αβT.
(1)求A的全部特征值与特征向量;
(2)问A能否相似于对角矩阵,说明理由.
8.3 设A是n 阶矩阵,且A的第i行、第j列的元素aij=i·j.
(1)求r(A);
(2)求A的特征值与特征向量与并问A 能否相似于对角矩阵,若能,求出一个对角矩阵;若不能,则说明理由.
8.4 设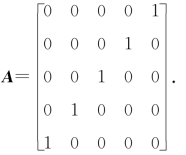
(1)求A的特征值与特征向量;
(2)求可逆矩阵P,使得P-1AP=Λ.
8.5 设
(1)求A的特征值与特征向量;
(2)求正交矩阵Q,使得QTAQ=Q-1AQ=Λ.
8.6 设A是3阶矩阵,b=[9,18,-18]T,方程组Ax=b有通解k1[-2,1,0]T+k2[2,0,1]T+[1,2,-2]T,其中k1,k2 是任意常数,求A及A100.
(1)求A的特征值;
(2)若A的对应于λ1=λ2=0的特征向量为ξ1=[1,1,0]T,ξ2=[2,2,0]T,ξ3=[0,2,1]T,ξ4=[5,-1,-3]T,求A的对应于λ3 的特征向量;
(3)在(2)的条件下,求矩阵A.
8.8 (1)设A,B是n阶矩阵,A有特征值λ=1,2,…,n,证明AB和BA有相同的特征值,且AB~BA;
(2)对一般的n阶矩阵A,B,是否必有AB~BA?说明理由.
8.9 已知A为2阶矩阵,α1 满足线性方程组Ax=x,α2 满足线性方程组Ax=x+α1,且α1,α2 线性无关.
(1)证明A不可相似对角化;
(2)若 ,求所有可逆矩阵P,使得P-1AP=B.
,求所有可逆矩阵P,使得P-1AP=B.
8.10 设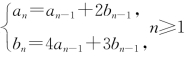 ,且
,且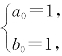 求a100,b100.
求a100,b100.
8.11 某试验性生产线每年一月份进行熟练工与非熟练工的人数统计,然后将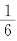 熟练工支援其他生产部门,其缺额由招收新的非熟练工补齐.新、老非熟练工经过培训及实践至年终考核有
熟练工支援其他生产部门,其缺额由招收新的非熟练工补齐.新、老非熟练工经过培训及实践至年终考核有 成为熟练工.设第n年一月份统计的熟练工和非熟练工所占百分比分别为xn 和yn,记成向量
成为熟练工.设第n年一月份统计的熟练工和非熟练工所占百分比分别为xn 和yn,记成向量
(1)求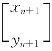 与
与 的关系式并写成矩阵形式
的关系式并写成矩阵形式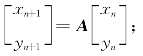
(2)验证 是A的两个线性无关的特征向量,并求出相应的特征值;
是A的两个线性无关的特征向量,并求出相应的特征值;
(3)当 时,求
时,求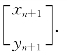
8.1 【解】应填E.
因A~Λ,可知存在可逆矩阵P,使得P-1AP=Λ,A=PΛP-1,则
f(A)=(PΛP-1)3-6(PΛP-1)2+11PΛP-1-5E
=P(Λ3-6Λ2+11Λ-5E)P-1=PEP-1=E.(www.chuimin.cn)
8.2 【解】(1)
故A有特征值λ=0(四重).
当λ=0时,由(0E-A)x=0,即Ax=0,其同解方程组为
3x1-2x2-x3+x4=0,
解得对应的线性无关特征向量为
ξ1=[2,3,0,0]T,ξ2=[1,0,3,0]T,ξ3=[1,0,0,-3]T.
故A的对应于特征值λ=0的全部特征向量为k1ξ1+k2ξ2+k3ξ3,其中k1,k2,k3 为不同时为零的任意常数.
(2)因 r(A)=r(αβT)≤r(α)=1(α≠0),
又A≠O,故r(A)=1.则四重特征值λ=0对应的线性无关的特征向量只有3个,故A 不能相似于对角矩阵.
8.3 【解】方法一 (1)由题设条件知
且 ,故r(A)=1.
,故r(A)=1.
(2)由A的特征多项式
知A有特征值λ1=λ2=…=λn-1=0,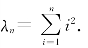
当λ1=λ2=…=λn-1=0时,方程组(0E-A)x=0就是方程组Ax=0,其同解方程组是x1+2x2+…+nxn=0,解得对应的线性无关特征向量为
ξ1=[-2,1,0,…,0]T,ξ2=[-3,0,1,0,…,0]T,…,ξn-1=[-n,0,…,0,1]T.
当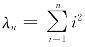 时,由(λnE-A)x=0,对系数矩阵作初等行变换,得
时,由(λnE-A)x=0,对系数矩阵作初等行变换,得
方程组(λnE-A)x=0的同解方程组为
得对应的特征向量为ξn=[1,2,…,n]T.
从而知A有n 个线性无关的特征向量,A~Λ,取
方法二 (1)由题设条件知,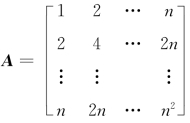 ,A中第i行元素是第1行的i倍,故有
,A中第i行元素是第1行的i倍,故有
其中α=[1,2,…,n]T≠0,故r(A)=1.
(2)因A2=(ααT)(ααT)=α(αTα)αT=(αTα)A= ,故知A 的特征值的取值范围为
,故知A 的特征值的取值范围为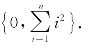
当λ=0时,对应的特征向量满足Ax=ααTx=0.因 ,在方程组ααTx=0两边左乘αT,得
,在方程组ααTx=0两边左乘αT,得
αT(ααTx)=(αTα)αTx=0,
得αTx=0.
若αTx=0时,两边左乘α,得ααTx=0,故方程组ααTx=0与αTx=0是同解方程组,故只需解方程组αTx=0,解得λ=0对应的线性无关的特征向量为
ξ1=[-2,1,0,…,0]T,ξ2=[-3,0,1,0,…,0]T,…,ξn-1=[-n,0,…,0,1]T.
又 ,故A有一个非零特征值
,故A有一个非零特征值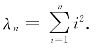
当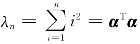 时,由(λnE-A)x=(αTαE-ααT)x=0,可观察知,当x=α时,有
时,由(λnE-A)x=(αTαE-ααT)x=0,可观察知,当x=α时,有
(αTαE-ααT)α=(αTα)α-(ααT)α=(αTα)α-α(αTα)=0,
故α=[1,2,…,n]T=ξn 是对应 的特征向量.
的特征向量.
即A有n 个线性无关的特征向量,A能相似于对角矩阵.下同方法一.
8.4 【解】(1)先求A的特征值.
方法一 由
得A的特征值为λ1=1(三重),λ2=-1(二重).
方法二 因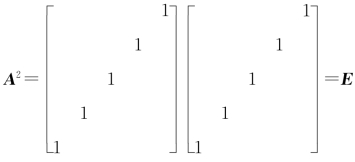 ,故A的特征值的取值范围为{1,-1}.
,故A的特征值的取值范围为{1,-1}.
下面求A的特征向量.
当λ1=1时,由(E-A)x=0,即
故线性无关的特征向量为ξ1=[1,0,0,0,1]T,ξ2=[0,1,0,1,0]T,ξ3=[0,0,1,0,0]T.
当λ2=-1时,由(-E-A)x=0,即
故线性无关的特征向量为ξ4=[0,1,0,-1,0]T,ξ5=[1,0,0,0,-1]T.
8.5 【解】(1)由特征方程,得
即A的特征值为λ1=2,λ2=-2(三重).
当λ1=2时,由(2E-A)x=0,即
得ξ1=[1,1,1,1]T(只有一个线性无关的特征向量).
当λ2=-2时,由(-2E-A)x=0,即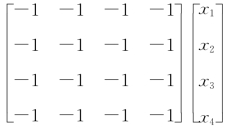 =0,其同解方程组为x1+x2+x3+x4=0,对应线性无关的特征向量(取正交特征向量)为
=0,其同解方程组为x1+x2+x3+x4=0,对应线性无关的特征向量(取正交特征向量)为
ξ2=[1,-1,0,0]T,ξ3=[1,1,-2,0]T,ξ4=[1,1,1,-3]T.
(当解得ξ2 后,求ξ3 时,令ξ3 与ξ2 正交,且满足方程组;当解得ξ2,ξ3,求ξ4 时,令ξ4 和ξ2,ξ3 正交,且满足方程组.)
(2)将ξ1,ξ2,ξ3,ξ4 单位化,合并成正交矩阵得
【注】(1)正交特征向量的取法不唯一,故Q不唯一.
(2)求λ2=-2(三重)对应的单位正交特征向量时,也可先求出线性无关的3个特征向量,再利用施密特正交化公式将其正交化,再和ξ1 一起单位化,且合并成正交矩阵.
(3)因A2=4E,故λ2=4,λ=±2,得A的特征值的取值范围,求对应的特征向量,再由线性无关特征向量的个数确定λi 的重数及正交矩阵.
(4)因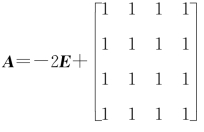 =-2E+B=-2E+ααT,其中B=ααT,α=[1,1,1,1]T.
=-2E+B=-2E+ααT,其中B=ααT,α=[1,1,1,1]T.
故B有特征值0(三重),4,从而A有特征值-2(三重),2.
8.6 【解】方法一 由题设条件知,对应齐次方程组的基础解系是ξ1=[-2,1,0]T,ξ2=[2,0,1]T,即ξ1,ξ2是A的对应于λ=0的两个线性无关的特征向量,又η=[1,2,-2]T是Ax=b的特解,即有
知ξ3=[1,2,-2]T=η是A 的对应于λ=9的特征向量,取可逆矩阵P=[ξ1,ξ2,ξ3],则
方法二 由方程组的通解直接求出系数矩阵A.
因对应齐次方程组Ax=0有通解为k1ξ1+k2ξ2=k1[-2,1,0]T+k2[2,0,1]T,故r(A)=1.可设方程组为
ax1+bx2+cx3=0,
将ξ1,ξ2 代入,则有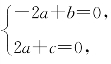 得c=-2a,b=2a,故方程组为
得c=-2a,b=2a,故方程组为
a(x1+2x2-2x3)=0.
对应的非齐次方程组为
将特解η=[1,2,-2]T代入得l1=1,l2=2,l3=-2.
故得对应矩阵
再求A100.(见方法一(*))
或因Aξ1=0,故A100ξ1=0;Aξ2=0,故A100ξ2=0.Aη=9η,故A100η=9100η,故
8.7 【解】(1)由A~B,则A,B有相同的秩和特征值.显然r(B)=1,B有特征值λ1=λ2=0且λ1+λ2+λ3= =1+4+9,得λ3=14,故A有特征值λ1=λ2=0,λ3=14.
=1+4+9,得λ3=14,故A有特征值λ1=λ2=0,λ3=14.
(2)λ1=λ2=0是A的二重特征值,对应的线性无关特征向量最多有两个,由题设知ξ1=[1,1,0]T,ξ3=[0,2,1]T线性无关(取ξ1,ξ2,ξ3,ξ4的一个极大线性无关组),故取η1=ξ1,η2=ξ3为λ1=λ2=0的特征向量.因A是实对称矩阵,将λ3=14对应的特征向量设为η3=[x1,x2,x3]T,则η3 与η1,η2 正交,则有ηT1η3=0,ηT2η3=0.即有
基础解系为η3=[1,-1,2]T,即是λ3=14对应的特征向量.
(3)方法一 由(2),令P=[η1,η2,η3],则
方法二 因与η3 正交的非零向量均是A的对应于λ=0的特征向量,取一个与η1=ξ1=[1,1,0]T,η3=[1,-1,2]T均正交的向量η2,可得η2=[1,-1,-1]T.
将η1,η2,η3 单位化,并合并成正交矩阵,得
【注】方法二用正交矩阵求A比用可逆矩阵求简单,且这里没有利用施密特正交化方法.
8.8 (1)【证】因A有n 个互不相同的非零特征值,|A|=n!≠0,故A可逆,从而有
|λE-AB|=|A(λA-1-B)|=|A||λE-BA||A-1|=|λE-BA|,
即AB和BA 有相同的特征多项式,故有相同的特征值.
又若取可逆矩阵P=A,则有P-1ABP=A-1ABA=BA,故有AB~BA.
(2)【解】一般地,AB不一定相似于BA.例如,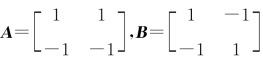 ,则有
,则有
显然 r(AB)=0,r(BA)=1,
故AB不相似于BA.
【注】(1)要证明相似,应找出可逆矩阵P,使得P-1ABP=BA.
(2)要说明可能不相似,只要举出一个反例即可.由(1)已知A 可逆时,必有AB~BA,故举反例时应举A是不可逆矩阵.
(3)相似必有相同的特征值,但特征值相同不一定相似.
8.9 (1)【证】由题意有Aα1=α1,Aα2=α2+α1,故[Aα1,Aα2]=[α1,α1+α2],即
记P=[α1,α2],B= ,于是有AP=PB,由题设知P可逆,故P-1AP=B,A与B 相似.
,于是有AP=PB,由题设知P可逆,故P-1AP=B,A与B 相似.
由 ,得λ1=λ2=1,故A的特征值也为1(二重).若A 可相似对角化,则存在可逆矩阵C,使得
,得λ1=λ2=1,故A的特征值也为1(二重).若A 可相似对角化,则存在可逆矩阵C,使得 ,得A=CEC-1=E,但P-1AP=P-1EP=E≠B,矛盾,于是A 不可相似对角化.
,得A=CEC-1=E,但P-1AP=P-1EP=E≠B,矛盾,于是A 不可相似对角化.
(2)【解】由(1)知(A-E)α1=0,又 ,故
,故
α1=k1[1,0]T=[k1,0]T,k1≠0.
又(A-E)α2=α1,[A-E┊α1]=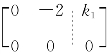 ,故
,故
则当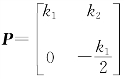 ,k1≠0,k2 为任意常数时,有P-1AP=B.
,k1≠0,k2 为任意常数时,有P-1AP=B.
8.10 【解】将递推关系表示成矩阵形式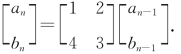
记 ,则ηn=Anη0.为求An,先求A的特征值、特征向量.由
,则ηn=Anη0.为求An,先求A的特征值、特征向量.由
故λ1=-1,λ2=5.
当λ1=-1时,由 ,得ξ1=[1,-1]Τ;
,得ξ1=[1,-1]Τ;
当λ2=5时,由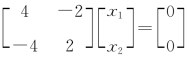 ,得ξ2=[1,2]Τ.
,得ξ2=[1,2]Τ.
8.11 【解】(1) 化简得
化简得 即
即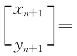
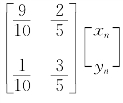 ,于是
,于是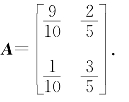
(2)令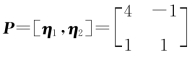 ,则由|P|=5≠0知,η1,η2 线性无关.
,则由|P|=5≠0知,η1,η2 线性无关.
因 ,故η1 为A的特征向量,且相应的特征值λ1=1;
,故η1 为A的特征向量,且相应的特征值λ1=1;
因 ,故η2 为A的特征向量,且相应的特征值
,故η2 为A的特征向量,且相应的特征值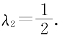
容易求得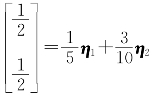 ,于是
,于是

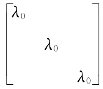 ,故r(A)=0.应选(A).
,故r(A)=0.应选(A).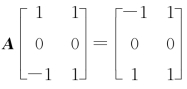 可得
可得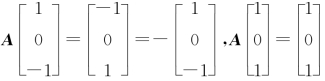 ,所以-1是A 的一个特征值,其对应的全部特征向量为
,所以-1是A 的一个特征值,其对应的全部特征向量为 (k
(k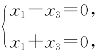 解得
解得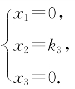
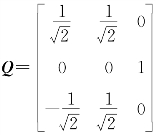 ,则Q
,则Q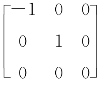 ,故
,故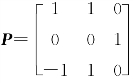 ,则
,则 可取α
可取α ,求正交矩阵C,使得C
,求正交矩阵C,使得C ,故
,故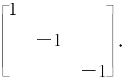
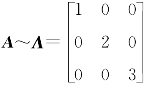 ,f(x)=x
,f(x)=x

 ,求所有可逆矩阵P,使得P
,求所有可逆矩阵P,使得P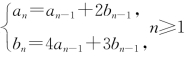 ,且
,且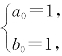 求a
求a
 与
与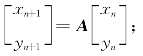
 是A的两个线性无关的特征向量,并求出相应的特征值;
是A的两个线性无关的特征向量,并求出相应的特征值; 时,求
时,求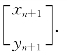

 ,故r(A)=1.
,故r(A)=1. ,A中第i行元素是第1行的i倍,故有
,A中第i行元素是第1行的i倍,故有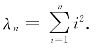
 ,故A的特征值的取值范围为{1,-1}.
,故A的特征值的取值范围为{1,-1}.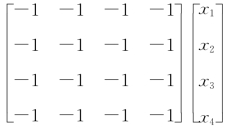 =0,其同解方程组为x
=0,其同解方程组为x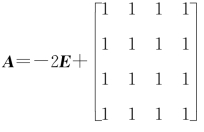 =-2E+B=-2E+αα
=-2E+B=-2E+αα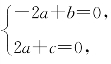 得c=-2a,b=2a,故方程组为
得c=-2a,b=2a,故方程组为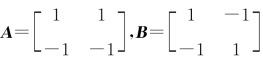 ,则有
,则有 ,于是有AP=PB,由题设知P可逆,故P
,于是有AP=PB,由题设知P可逆,故P ,得λ
,得λ ,得A=CEC
,得A=CEC ,故
,故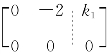 ,故
,故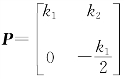 ,k
,k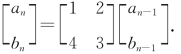
 ,则η
,则η ,得ξ
,得ξ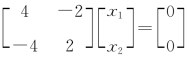 ,得ξ
,得ξ 化简得
化简得 即
即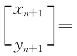
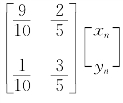 ,于是
,于是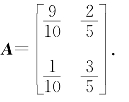
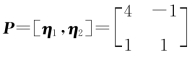 ,则由|P|=5≠0知,η
,则由|P|=5≠0知,η ,故η
,故η ,故η
,故η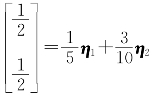 ,于是
,于是





相关推荐