首页理论教育线性代数重要结论：A与B的关系及其应用

线性代数重要结论：A与B的关系及其应用

2023-11-21 理论教育版权反馈

【摘要】：（1）A～BAT～BT，A－1～B－1，A*～B*（后面两个要求A可逆）.（2）A～BAm～Bm，f（A）～f（B）.【注】由P－1AmP＝Bm，P－1f（A）P＝f（B），有Am＝PBmP－1，f（A）＝Pf（B）P－1.若B＝Λ，则Am＝PΛmP－1，f（A）＝Pf（Λ）P－1.见例8.8，例8.9.（3）A～B，B～ΛA～Λ.【注】P－1AP＝B，Q－1BQ＝ΛQ－1P－1APQ＝Λ（PQ）

（1）A～B⇒AT～BT，A－1～B－1，A*～B*（后面两个要求A可逆）.

（2）A～B⇒Am～Bm，f（A）～f（B）.

【注】由P－1AmP＝Bm，P－1f（A）P＝f（B），有Am＝PBmP－1，f（A）＝Pf（B）P－1.若B＝Λ，则Am＝PΛmP－1，f（A）＝Pf（Λ）P－1.

见例8.8，例8.9.

（3）A～B，B～Λ⇒A～Λ.

【注】P－1AP＝B，Q－1BQ＝Λ⇒Q－1P－1APQ＝Λ⇒（PQ）－1APQ＝Λ，令PQ＝C，则C－1AC＝Λ，考试可求C.

见例8.10.

（4）A～Λ，B～Λ⇒A～B.

【注】P－1AP＝Λ，Q－1BQ＝Λ⇒P－1AP＝Q－1BQ⇒QP－1APQ－1＝B⇒（PQ－1）－1APQ－1＝B.令PQ－1＝C，则C－1AC＝B，考试可求C.

见例8.11.

（5）A～C，B～D⇒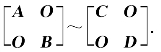 pagenumber_ebook=160,pagenumber_book=152

例8.8 已知A是3阶矩阵，且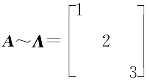 pagenumber_ebook=160,pagenumber_book=152 .设B＝A3－6A2＋11A－E，则B＝________.

【解】应填5E.

由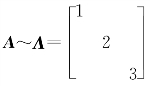 pagenumber_ebook=160,pagenumber_book=152 知，存在可逆矩阵P，使P－1AP＝Λ，A＝PΛP－1，则

例8.9 已知矩阵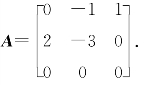 pagenumber_ebook=160,pagenumber_book=152

（1）求A99；

（2）设3阶矩阵B＝［α1，α2，α3］满足B2＝BA.记B100＝［β1，β2，β3］，将β1，β2，β3 分别表示为α1，α2，α3 的线性组合.

【解】（1）因为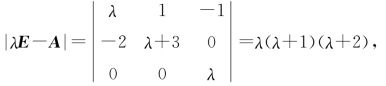 pagenumber_ebook=160,pagenumber_book=152

所以A的特征值为λ1＝－1，λ2＝－2，λ3＝0.

当λ1＝－1时，解方程组（－E－A）x＝0，得特征向量ξ1＝［1，1，0］T；

当λ2＝－2时，解方程组（－2E－A）x＝0，得特征向量ξ2＝［1，2，0］T；

当λ3＝0时，解方程组Ax＝0，得特征向量ξ3＝［3，2，2］T.

（2）因为B2＝BA，所以

例8.10 设A，P均为3阶矩阵，P＝［γ1，γ2，γ3］，其中γ1，γ2，γ3 为3维列向量且线性无关，若A［γ1，γ2，γ3］＝［γ3，γ2，γ1］.

（1）证明A可相似对角化；

（2）若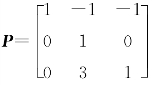 pagenumber_ebook=161,pagenumber_book=153 ，求可逆矩阵C，使得C－1AC＝Λ，并写出对角矩阵Λ.

（1）【证】A［γ1，γ2，γ3］＝［γ1，γ2，γ3］ pagenumber_ebook=161,pagenumber_book=153 ，令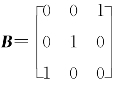，即AP＝PB⇒P－1AP＝B⇒A～B.

对矩阵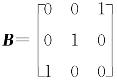 pagenumber_ebook=161,pagenumber_book=153 ，由(www.chuimin.cn)

得特征值λ1＝λ2＝1，λ3＝－1.

当λ1＝λ2＝1时，由（E－B）x＝0，即

解得基础解系ξ1＝［1，0，1］T，ξ2＝［0，1，0］T.

当λ3＝－1时，由（－E－B）x＝0，即

解得基础解系为ξ3＝［1，0，－1］T.

记 pagenumber_ebook=162,pagenumber_book=154 ，则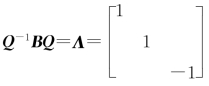，故B可相似对角化，B～Λ，由传递性，知A～Λ.

（2）【解】由（1）知，Q－1（P－1AP）Q＝Λ⇒（PQ）－1A（PQ）＝Λ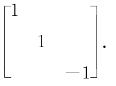＝ pagenumber_ebook=162,pagenumber_book=154

令 pagenumber_ebook=162,pagenumber_book=154 ，即为所求.

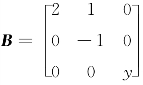例8.11 已知矩阵 pagenumber_ebook=162,pagenumber_book=154 与相似.

（1）求x，y；

（2）求可逆矩阵P使得P－1AP＝B.

【解】（1）因为矩阵A与B 相似，所以tr（A）＝tr（B），|A|＝|B|，即

解得x＝3，y＝－2.

（2）矩阵B的特征多项式为

|λE－B|＝（λ－2）（λ＋1）（λ＋2），

所以B的特征值为2，－1，－2.

由于A与B 相似，所以A的特征值也为2，－1，－2.

A的属于特征值2的特征向量为ξ1＝［1，－2，0］T；

A的属于特征值－1的特征向量为ξ2＝［－2，1，0］T；

A的属于特征值－2的特征向量为ξ3＝［1，－2，－4］T.

记P1＝［ξ1，ξ2，ξ3］，于是

B的属于特征值2的特征向量为η1＝［1，0，0］T；

B的属于特征值－1的特征向量为η2＝［1，－3，0］T；

B的属于特征值－2的特征向量为η3＝［0，0，1］T.

记P2＝［η1，η2，η3］，于是

由P－11 AP1＝P－12 BP2，得（P1P－12）－1A（P1P－12）＝B.令

则P－1AP＝B.