张宇线性代数9讲：A的相似对角化

2023-11-21 理论教育版权反馈

【摘要】：设n阶矩阵A，若存在n阶可逆矩阵P，使得P－1AP＝Λ，其中Λ 是对角矩阵，则称A可相似对角化，记A～Λ，称Λ 是A 的相似标准形.于是可知，若A可相似对角化，即P－1AP＝Λ，其中P可逆，等式两边同时左乘P，有AP＝PΛ，记由P可逆，则ξ1，ξ2，…＝λn＝0，A的特征值全是零.若A能与对角矩阵Λ 相似，则Λ 的主对角线元素为A

设n阶矩阵A，若存在n阶可逆矩阵P，使得P－1AP＝Λ，其中Λ 是对角矩阵，则称A可相似对角化，记A～Λ，称Λ 是A 的相似标准形.

于是可知，若A可相似对角化，即P－1AP＝Λ，其中P可逆，等式两边同时左乘P，有AP＝PΛ，记

由P可逆，则ξ1，ξ2，…，ξn 线性无关.上述过程可逆，于是，n阶矩阵A 可相似对角化⇔A有n 个线性无关的特征向量.据此，可得以下结论.

设A为n 阶矩阵.

（1）充要条件.

①A有n 个线性无关的特征向量⇔A～Λ.

②ni＝n－r（λiE－A）⇔A～Λ.

【注】（1）λi 是ni 重根，故n－r（λiE－A）表示（λiE－A）x＝0的解中线性无关的向量个数，也即属于λi 的线性无关的特征向量的个数.当ni＝n－r（λiE－A）时，即知A有n 个线性无关的特征向量，等价于上面的①.

（2）②常用于求秩.

见例8.1，例8.2.

（2）充分条件.

①A是实对称矩阵⇒A～Λ.

【注】A是实对称矩阵，则A必有n 个线性无关的特征向量，故A～Λ.

②A有n 个互异特征值⇒A～Λ.

【注】由于不同特征值对应的特征向量线性无关，故当A有n 个互异特征值时，A 必有n 个线性无关的特征向量，故A～Λ.

见例8.1.

③A2＝A⇒A～Λ.（证明见例8.3）

④A2＝E⇒A～Λ.（证明见例8.4）

⑤r（A）＝1且tr（A）≠0⇒A～Λ.（证明见例8.5）

（3）必要条件.

A～Λ⇒r（A）＝非零特征值的个数（重根按重数算）.

（4）否定条件.

①A≠O，Ak＝O（k为大于1的整数）⇒A不可相似对角化.（证明见例8.6）

②A的特征值全为k但A≠kE⇒A不可相似对角化.（证明见例8.7）

例8.1 设 pagenumber_ebook=155,pagenumber_book=147

（1）求A的特征值；

（2）a取何值时，A可以相似对角化.

于是A的特征值为1－a，a，1＋a.

（2）在1－a，a，1＋a中，a≠1＋a，而分别令，1－a＝1＋a⇔a＝0.于是当a≠0和时，A的特征值1－a，a，1＋a两两都不相等，此时A可以相似对角化.

如果a＝0，则A的特征值为1，1，0.而

即r（E－A）＝2，3－r（E－A）＝1，于是对二重特征值1没有两个线性无关的特征向量，从而A不可相似对角化.

如果，则A的特征值为.而

即，于是对二重特征值没有两个线性无关的特征向量，从而A 不可相似对角化.

例8.2 设矩阵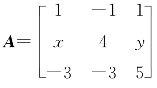 pagenumber_ebook=156,pagenumber_book=148 ，已知A有3个线性无关的特征向量，λ＝2是A 的2重特征值.求可逆矩阵P，使得P－1AP为对角矩阵.

【解】因为A有3个线性无关的特征向量，λ＝2是A的2重特征值，所以A 的属于λ＝2的线性无关的特征向量必有2个，故r（2E－A）＝1.

经过初等行变换，得

于是，解得x＝2，y＝－2，即

其特征多项式

由此得特征值λ1＝λ2＝2，λ3＝6.

对于特征值λ1＝λ2＝2，解齐次线性方程组（2E－A）x＝0，有(www.chuimin.cn)

对应的特征向量为

ξ1＝［1，－1，0］T，ξ2＝［1，0，1］T.

对于特征值λ3＝6，解齐次线性方程组（6E－A）x＝0，有

对应的特征向量为

ξ3＝［1，－2，3］T.

令可逆矩阵

则有

例8.3 设n阶方阵A 满足A2＝A，证明A可以相似对角化.

【证】设λ是A 的特征值，ξ（≠0）是A的属于λ的特征向量，则Aξ＝λξ，由第7讲“二（3）”的“②”，根据A2＝A，有

λ2－λ＝0.

故λ＝0或λ＝1，A的特征值的取值范围是｛0，1｝.

由第4讲“二（11）”知，若A为n 阶方阵，且A2＝A，则r（A）＋r（E－A）＝n.现设r（A）＝r，则齐次线性方程组（0E－A）x＝0的基础解系中有n－r个线性无关的解向量，所以A的属于0的线性无关的特征向量有n－r个，记为ξ1，ξ2，…，ξn－r，且r（E－A）＝n－r.齐次线性方程组（E－A）x＝0的基础解系中有n－（nr）＝r个线性无关的解向量，所以A的属于1的线性无关的特征向量有r个，记为η1，η2，…，ηr.因0和1是不同的特征值，所以ξ1，ξ2，…，ξn－r，η1，η2，…，ηr 线性无关.从而n阶方阵A 有n 个线性无关的特征向量，所以A可相似对角化.

例8.4 设n阶方阵A 满足A2＝E，证明A可以相似对角化.

【证】与例8.3类似，由第7讲“二（3）”的“②”，根据A2＝E，有λ2＝1，故A 的特征值的取值范围是｛1，－1｝.

又由第4讲“二（12）”，若A为n 阶方阵，A2＝E，则

r（A－E）＋r（A＋E）＝n，

可推得A有n 个线性无关的特征向量，从而证得A可以相似对角化.

【注】强调一下，若A2＝E，则λ2＝1，λ＝±1，只能说A 的特征值的取值范围是｛1，－1｝，即A 的特征值可能全为1，可能为1和－1，也可能全为－1，如，

都满足A2＝E.故考生一定不要因为λ2＝1，就武断地说，λ1＝1，λ2＝－1.这是典型的错误.

例8.5 设n阶矩阵

已知tr（A）＝a≠0.证明：矩阵A可以相似对角化.

【证】设α＝［a1，a2，…，an］T，β＝［b1，b2，…，bn］T，则矩阵A＝αβT.于是

设λ是A 的特征值，ξ（≠0）是A的属于λ的特征向量，则由A2＝aA，由第7讲“二（3）”的“②”，有λ2＝aλ，即λ（λ－a）＝0，故A的特征值的取值范围是｛0，a｝.又 pagenumber_ebook=158,pagenumber_book=150 ，所以λ1＝a是A 的一重特征值，λ2＝λ3＝…＝λn＝0是A的n－1重特征值.

对于特征值λ2＝λ3＝…＝λn＝0，齐次线性方程组（0E－A）x＝0的系数矩阵的秩

r（0E－A）＝r（－A）＝r（A）

＝r（αβT）≤min｛r（α），r（βT）｝＝1.

又因为，故aibi（i＝1，2，…，n）不全为零.由此可知

r（A）≥1，

所以r（0E－A）＝1.因此，矩阵A的属于n－1重特征值0的线性无关的特征向量个数为n－1.从而，A有n个线性无关的特征向量，故A可以相似对角化.

例8.6 设A是n 阶非零矩阵，若存在正整数k（k＞1）使得Ak＝O，证明A不可相似对角化.

【证】设λ是A 的特征值，ξ（≠0）是A 的属于λ 的特征向量，则Aξ＝λξ，由第7讲“二（3）”的“②”，Ak＝O，故λk＝0，即λ1＝λ2＝…＝λn＝0，A的特征值全是零.

若A能与对角矩阵Λ 相似，则Λ 的主对角线元素为A 的全部特征值λ1，λ2，…，λn.而λ1＝λ2＝…＝λn＝0，于是Λ＝O，即存在可逆矩阵P，使得

A＝PΛP－1＝POP－1＝O，

这与题设A≠O矛盾，故A不可相似对角化.

【注】若懂得了例8.6 的道理，命题中若出现 pagenumber_ebook=158,pagenumber_book=150 ，而它们本身不是零矩阵，则可直接判别出其不可相似对角化.

例8.7 设 pagenumber_ebook=158,pagenumber_book=150 ai与bi（i＝1，2，3）均不全为零，证明A，B均不可相似对角化.

【证】由|λE－A|＝0，|λE－B|＝0，知A，B 的特征值全为k.若A，B 均能与对角矩阵Λ 相似，则Λ＝kE，即存在可逆矩阵P，Q，使得P－1AP＝Λ＝kE，Q－1BQ＝Λ＝kE，也即A＝P（kE）P－1＝kE，B＝Q（kE）Q－1＝kE，这与题设ai与bi（i＝1，2，3）均不全为零矛盾，故A，B均不可相似对角化.

【注】若懂得了例8.7的道理，命题中若出现 pagenumber_ebook=158,pagenumber_book=150 等，均可直接判别出其不可相似对角化.

张宇线性代数9讲：A的相似对角化

相关推荐