线性代数的一种方法:用秩命题

若r（A）＝1，则λ1＝…＝λn－1＝0，λn＝tr（A），且ξ1，…，ξn－1 是n－1重特征值λ＝0的线性无关的特征向量.

例7.2 设A为n 阶正交矩阵，证明：

（1）若|A|＝－1，则－1是A的特征值；

（2）若n为奇数，且|A|＝1，则1是A的特征值.

【证】（1）因为A为正交矩阵，故AT＝A－1，由题意|A|＝－1，于是

|－E－A|＝|－AAT－A|＝|A（－AT－E）|

＝|A||（－E－A）T|＝－|－E－A|，

所以|－E－A|＝0，故－1是A的特征值.

（2）因为AT＝A－1，且n为奇数，|A|＝1，于是

|E－A|＝|AAT－A|＝|A（AT－E）|＝|A||－（E－A）T|

＝（－1）n|A||E－A|＝－|E－A|，

所以|E－A|＝0，故1是A的特征值.

例7.3 设A是3阶矩阵，|A|＝3，且满足|A2＋2A|＝0，|2A2＋A|＝0，则A11＋A22＋A33＝________.

【解】应填

由题设，|A2＋2A|＝|A（A＋2E）|知|A||A＋2E|＝0，因|A|＝3≠0，则|A＋2E|＝0，故A有特征值λ1＝－2.

又，即，得A有特征值

因|A|＝3＝λ1λ2λ3，故λ3＝3.

由本讲“二（3）”的“①”，知，即A的特征值为，即A有特征值μ3＝1，由第2讲的“三”知，

例7.4 设矩阵，且|A|＝－1，A的伴随矩阵A有特征值λ0，属于λ0的

特征向量为α＝［－1，－1，1］T，求a，b，c及λ0 的值.

【解】Aα＝λ0α，两端左乘A，得AAα＝|A|α＝－α＝λ0Aα，即

由此得

由①－③解得λ0＝1，代入①，②式得b＝－3，a＝c.

由|A|＝－1，a＝c，b＝－3，有

得a＝c＝2，故a＝2，b＝－3，c＝2，λ0＝1.

例7.5 已知是矩阵A属于特征值λ＝1的特征向量，α2，α3是矩阵A属

于特征值λ＝3的线性无关的特征向量，则矩阵P不可以是（）.

（A）［α1，－2α2，α3］ （B）［α1，α2＋α3，α2－2α3］

（C）［α1，α3，α2］ （D）［α1＋α2，α1－α2，α3］

【解】应选（D）.

若则有AP＝PΛ，即

由此，

αi 是矩阵A属于特征值ai（i＝1，2，3）的特征向量，又因矩阵P可逆，因此，α1，α2，α3 线性无关.

若α是属于特征值λ的特征向量，则－2α仍是属于特征值λ的特征向量，故（A）正确.

若α，β是属于特征值λ的特征向量，则k1α＋k2β（k1，k2不同时为零）仍是属于特征值λ的特征向量.本题中，α2，α3 是属于λ＝3的线性无关的特征向量，故α2＋α3，α2－2α3 仍是属于λ＝3的特征向量，并且α2＋α3，α2－2α3 线性无关，故（B）正确.

关于（C），因为α2，α3 均是λ＝3的特征向量，所以α2，α3 谁在前谁在后均正确，即（C）正确.

由于α1，α2 是不同特征值的特征向量，因此α1＋α2，α1－α2 不再是矩阵A的特征向量，故（D）不正确.

例7.6 设A为3阶矩阵，P为3阶可逆矩阵，且.若P＝［α1，α2，α3］，Q＝［α1＋α2，α2，α3］，则Q－1AQ＝（）.

【解】应选（B）.

由题设知，矩阵A是可相似对角化的矩阵，因而其相似变换矩阵P的列向量α1，

α2，α3 是A的分别属于特征值λ1＝1，λ2＝1，λ3＝2的特征向量.由于λ1＝λ2＝1是A的2重特征值，所以α1＋α2 仍是A的属于特征值1的特征向量，即A（α1＋α2）＝1（α1＋α2），从而有

应选（B）.

例7.7 设A，B，C均是3阶矩阵，满足AB＝－2B，CAT＝2C.其中

（1）求A；

（2）证明：对任何3维列向量ξ，A100ξ与ξ 必线性相关.

（1）【解】由题设条件：①AB＝－2B，将B 按列分块，设B＝［β1，β2，β3］，则有A［β1，β2，β3］＝－2［β1，β2，β3］，即Aβi＝－2βi，i＝1，2，3，故βi（i＝1，2，3）是A的属于λ＝－2的特征向量.又因β1，β2 线性无关，β3＝β1＋β2，故β1，β2 是A的属于λ＝－2的线性无关的特征向量.

②CAT＝2C，两边转置得ACT＝2CT，将CT按列分块，设CT＝［α1，α2，α3］，则有

A［α1，α2，α3］＝2［α1，α2，α3］，Aαi＝2αi，i＝1，2，3，

故αi（i＝1，2，3）是A的属于λ＝2的特征向量.因α1，α2，α3 互成比例，故α1 是A的属于特征值λ＝2的特征向量.

取P＝［β1，β2，α1］，则P可逆，且

（2）【证】因Aβi＝－2βi（i＝1，2），故A100βi＝（－2）100βi＝2100βi（i＝1，2）.

因Aα1＝2α1，故A100α1＝2100α1.

对任意的3维列向量ξ，因β1，β2，α1 线性无关，ξ可由β1，β2，α1 线性表示，且表示法唯一.

设ξ＝μ1β1＋μ2β2＋μ3α1，则

A100ξ＝A100（μ1β1＋μ2β2＋μ3α1）＝μ1A100β1＋μ2A100β2＋μ3A100α1

＝μ12100β1＋μ22100β2＋μ32100α1＝2100（μ1β1＋μ2β2＋μ3α1）＝2100ξ.

得证A100ξ和ξ 成比例，A100ξ和ξ 线性相关.

例7.8 设向量组α，Aα，A2α线性无关，其中A为3阶矩阵，α为3维非零列向量，且A3α＝3Aα－2A2α，求A的特征值.

【解】令P＝［α，Aα，A2α］，因α，Aα，A2α线性无关，所以P可逆，且

其中则A＝PBP－1，即A与B 相似，从而A，B有相同的特征值，又

知B的特征值为0，1，－3，故A的特征值为0，1，－3.

例7.9 设A是3阶实对称矩阵，已知A的每行元素之和为3，且有二重特征值λ1＝λ2＝1.求A的全部特征值、特征向量，并求An.

【解】方法一 A是3阶矩阵，每行元素之和为3，即有

故知A有特征值λ3＝3，对应的特征向量为ξ3＝［1，1，1］T，所以对应于λ3＝3的全部特征向量为k3ξ3（k3为任意非零常数）.

又A是实对称矩阵，不同特征值对应的特征向量相互正交，故设λ1＝λ2＝1对应的特征向量为ξ＝［x1，x2，x3］T，应有

ξT3ξ＝x1＋x2＋x3＝0，

解得λ1＝λ2＝1的线性无关特征向量为

ξ1＝［－1，1，0］T，ξ2＝［－1，0，1］T.

所以对应于λ1＝λ2＝1的全部特征向量为k1ξ1＋k2ξ2（k1，k2 为不全为零的任意常数）.

其中P－1可如下求得.

方法二 由方法一，得Aξ3＝λ3ξ3，其中λ3＝3，ξ3＝［1，1，1］T.所以对应于λ3＝3的全部特征向量为k3ξ3（k3 为任意非零常数）.

设λ1＝λ2＝1对应的特征向量为ξ＝［x1，x2，x3］T，则应有

ξT3ξ＝x1＋x2＋x3＝0.

取ξ1＝［1，－1，0］T，再取ξ2 与ξ1 正交，设ξ2＝［1，1，x］T，代入上式得ξ2＝［1，1，－2］T，所以对应于λ1＝λ2＝1的全部特征向量为k1ξ1＋k2ξ2（k1，k2 为不全为零的任意常数）.

将ξ1，ξ2，ξ3 单位化，并取正交矩阵

【注】因A是实对称矩阵，故不同特征值对应的特征向量相互正交，且不仅存在可逆矩阵P，使P－1AP＝Λ，还存在正交矩阵Q，使

Q－1AQ＝QTAQ＝Λ.

方法二中利用正交矩阵Q有Q－1＝QT，避免了用初等变换求逆，较简便.

例7.10 设A为3阶实对称矩阵，A的特征值λ1＝1，λ2＝2分别对应特征向量ξ1＝［1，a＋1，2］T，ξ2＝［a－1，－a，1］T，A的迹tr（A）＝2，η＝［2，－5a，2a＋1］T是A的属于特征值μ的特征向量，求a与μ的值，并求A.

【解】由tr（A）＝2，知λ1＋λ2＋λ3＝2，则A的第3个特征值λ3＝－1，并设其对应的特征向量ξ3＝［x1，x2，x3］T.因A为实对称矩阵，则ξ1，ξ2，ξ3 两两正交，即

由（）式解得a＝1或a＝－1.

当a＝1时，方程组为

其通解为k1［－4，1，1］T，取ξ3＝［－4，1，1］T.

又由本讲知识点“二（3）”的“①”中的表格知，当A的特征值与特征向量分别为λ（≠0）与ξ时，A的特征值与特征向量分别为与ξ，又，即，此时

设存在数k1，k2，k3，使k1ξ1＋k2ξ2＋k3ξ3＝η，即解此非齐次方程组，得唯一解

由本讲知识点的“三（2）”的“④”知，η不是A的特征向量，也就不是A的特征向量，故a＝1不符合题意，应舍去.

当a＝－1时，同理可得

显然，η＝－ξ3，由，得

即，也即Aξ3＝2ξ3，于是μ＝2.

综上所述，a＝－1，μ＝2.

令并记Q＝［γ1，γ2，γ3］，即Q为正交矩阵，QT＝Q－1，于是QTAQ＝Λ，则

7.1 设是3阶可逆矩阵，B是3阶矩阵，满足

则B有特征值（）.

（A）1，－1，－4 （B）1，1，4 （C）1，2，－2 （D）1，2，2

7.2 设A，P均为n阶可逆矩阵，λ，ξ分别是A 的特征值和对应的特征向量，则P－1AP的特征值和对应的特征向量分别是（）.

（A）（B）（C）（D）

7.3 设A是3阶矩阵，Ax＝0有通解k1ξ1＋k2ξ2，Aξ3＝ξ3（ξ3≠0），则存在可逆矩阵P，使得，其中P是（）.

（A）［ξ1，ξ2，ξ1＋ξ3］ （B）［ξ2，ξ3，ξ1］(https://www.chuimin.cn)

（C）［ξ1＋ξ2，－ξ2，2ξ3］ （D）［ξ1＋ξ2，ξ2－ξ3，ξ3］

7.4 设，其中abc＝－6，A是A的伴随矩阵，则A有非零特征值________.

7.5 设A是n 阶矩阵，λ，μ是实数，ξ是n 维非零列向量.

（1）若Aξ＝λξ，求A2的特征值、特征向量；

（2）若A2ξ＝μξ，问ξ是否必是A 的特征向量，说明理由；

（3）若A可逆，且有A3ξ＝λξ，A5ξ＝μξ，证明ξ是A 的特征向量，并指出其对应的特征值.

7.6 设A是3阶矩阵，有特征值λ1＝λ2＝2，对应两个线性无关的特征向量为ξ1，ξ2，λ3＝－2对应的特征向量为ξ3.

（1）问ξ1＋ξ2 是否是A的特征向量？说明理由；

（2）问ξ2＋ξ3 是否是A的特征向量？说明理由；

（3）证明：任意3维非零列向量β都是A2的特征向量，并求对应的特征值.

7.7 设A是3阶矩阵，有特征值λ1＝λ2＝－2，λ3＝2，对应的特征向量分别是ξ1＝［1，－2，2］T，ξ2＝［2，－5，3］T，ξ3＝［2，1，5］T，又向量β＝［3，11，11］T.

证明β是A100的特征向量，并求对应的特征值.

7.8 设A是3阶矩阵，λ1，λ2，λ3是A的3个不同的特征值，对应的特征向量分别是ξ1，ξ2，ξ3，令β＝ξ1＋ξ2＋ξ3.

（1）证明β不是A 的特征向量；

（2）证明向量组β，Aβ，A2β线性无关.

7.9 设有特征向量

（1）求A的特征向量ξi（i＝1，2，3）对应的特征值；

（2）求Ax＝ξ3 的通解；

（3）求A.

7.1 【解】应选（C）.

由题设条件得

又A是可逆矩阵，故有，即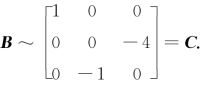

相似矩阵有相同的特征值，故C和B 有相同的特征值.

因为＝（λ－1）（λ－2）（λ＋2），故B有特征值为λ1＝1，λ2＝2，λ3＝－2，故应选（C）.

或由，两边取行列式，得，故应选（C）.

7.2 【解】应选（A）.

由题设条件

其中A可逆，故λ≠0，（）式左乘A，得

（）式左乘P－1，得

故知P－1AP有特征值，对应的特征向量为P－1ξ.故应选（A）.

【注】P－1AP相似于A，应有相同的特征值，再求P－1AP的特征向量也是方便的.

7.3 【解】应选（C）.

由题设，可知ξ1，ξ2 是A的对应于λ1＝λ2＝0的线性无关特征向量，ξ3 是A 的对应于λ3＝1的特征向量，且注意下列结论.

①A的同一个特征值如λ1＝λ2＝0对应的特征向量ξ1，ξ2，则k1ξ1＋k2ξ2 为非零向量时，k1ξ1＋k2ξ2 仍是λ1＝λ2＝0对应的特征向量.若ξ3 是λ3＝1对应的特征向量，则kξ3（k≠0）仍是λ3＝1对应的特征向量.

②对于不同的特征值，其对应的特征向量之和，如ξ1＋ξ3，ξ2－ξ3 等不再是A的特征向量.

③P中的特征向量排列次序应与对角矩阵中λi（i＝1，2，3）的排列次序一致.

由上述三条知应选（C）.因（C）中，ξ1＋ξ2，－ξ2 仍是对应于λ1＝λ2＝0的特征向量，2ξ3 仍是对应于λ3＝1的特征向量，且与对角矩阵中特征值的排列次序一致.

（A）中，ξ1＋ξ3 不是A的特征向量，（D）中，ξ2－ξ3 不是A的特征向量，（B）中，ξ3，ξ1 与对角矩阵中对应的特征值的排列次序不一致，故都是错误的.

7.4 【解】应填11.

因abc＝－6，故＝6＋abc＝0，r（A）＜3.

又＝6≠0，故r（A）＝2，r（A）＝1.

故A有特征值λ1＝λ2＝0，

7.5 【解】（1）由题设条件 Aξ＝λξ，

两边左乘A，得 A2ξ＝λAξ＝λ2ξ，

故A2有特征值λ2，对应的特征向量为ξ.

（2）ξ不一定是A 的特征向量.例如，故任意2维非零列向量都是A2的对应于特征值0的特征向量.取，是A2的特征向量，但不是A的特征向量，因

（）式左乘A3，得A6ξ＝λA3ξ＝λ2ξ；

（）式左乘A，得A6ξ＝μAξ.

故有

μAξ＝λ2ξ，

又因A可逆，故A5可逆，其对应的特征值μ≠0，从而有，故ξ是A 的特征向量，且其对应的特征值为

7.6 【解】（1）ξ1＋ξ2 仍是A的对应于λ1＝λ2＝2的特征向量.

由题设知Aξ1＝2ξ1，Aξ2＝2ξ2，故

A（ξ1＋ξ2）＝Aξ1＋Aξ2＝2ξ1＋2ξ2＝2（ξ1＋ξ2）.

（2）ξ2＋ξ3 不是A的特征向量.

假设ξ2＋ξ3 是A的特征向量，设其对应的特征值为μ，则有

A（ξ2＋ξ3）＝μ（ξ2＋ξ3），

得 2ξ2－2ξ3－μξ2－μξ3＝（2－μ）ξ2－（2＋μ）ξ3＝0，

因2－μ和2＋μ不同时为零，故ξ2，ξ3 线性相关，这与不同特征值对应的特征向量线性无关矛盾，故ξ2＋ξ3不是A的特征向量.

（3）因A有特征值λ1＝λ2＝2，λ3＝－2，故A2有特征值μ1＝μ2＝μ3＝4，对应的特征向量仍是ξ1，ξ2，ξ3，且ξ1，ξ2，ξ3 线性无关.故存在可逆矩阵P＝［ξ1，ξ2，ξ3］，使得

P－1A2P＝4E，A2＝P（4E）P－1＝4E，

从而对任意的β≠0，有A2β＝4Eβ＝4β，故知任意3维非零列向量β都是A2的对应于μ1＝μ2＝μ3＝4的特征向量.

7.7 【证】本题要证A100β＝λβ，并求出其中的λ.

将β用ξ1，ξ2，ξ3 线性表出，设

将增广矩阵作初等行变换.

解得［x1，x2，x3］T＝［1，－2，3］T，即β＝ξ1－2ξ2＋3ξ3.

由Aξi＝λiξi，知A100ξi＝λi100ξi，i＝1，2，3.故

A100β＝A100（ξ1－2ξ2＋3ξ3）＝（－2）100ξ1－2（－2）100ξ2＋3·2100ξ3

＝2100（ξ1－2ξ2＋3ξ3）＝2100β.

故β是A100的特征向量，且对应的特征值为2100.

【注】不必直接求出A100，利用Akξ＝λkξ 的关系可简化计算.

7.8 【证】（1）已知Aβ＝A（ξ1＋ξ2＋ξ3）＝λ1ξ1＋λ2ξ2＋λ3ξ3.

若β是A 的特征向量，设其对应的特征值为μ，则有

Aβ＝μβ＝μ（ξ1＋ξ2＋ξ3）＝λ1ξ1＋λ2ξ2＋λ3ξ3，

从而得（μ－λ1）ξ1＋（μ－λ2）ξ2＋（μ－λ3）ξ3＝0.

由于ξ1，ξ2，ξ3 是不同特征值对应的特征向量，故ξ1，ξ2，ξ3 线性无关，从而得λ1＝λ2＝λ3＝μ，这与λ1，λ2，λ3 互不相同矛盾.故β＝ξ1＋ξ2＋ξ3 不是A的特征向量.

（2）方法一 用线性无关的定义证.

设有数k1，k2，k3 使得 k1β＋k2Aβ＋k3A2β＝0.

由β＝ξ1＋ξ2＋ξ3 及Aξi＝λiξi，i＝1，2，3，代入得

k1（ξ1＋ξ2＋ξ3）＋k2（λ1ξ1＋λ2ξ2＋λ3ξ3）＋k3（λ21ξ1＋λ22ξ2＋λ23ξ3）＝0，

整理得 （k1＋k2λ1＋k3λ21）ξ1＋（k1＋k2λ2＋k3λ22）ξ2＋（k1＋k2λ3＋k3λ23）ξ3＝0.

因ξ1，ξ2，ξ3 线性无关，上式成立当且仅当

又λ1，λ2，λ3 互不相同，故方程组（）的系数行列式

故方程组（）仅有零解，即k1＝k2＝k3＝0，所以β，Aβ，A2β线性无关.

方法二 因

其中，所以C是可逆矩阵.

故r（β1，Aβ，A2β）＝r（ξ1，ξ2，ξ3）＝3.因此，β，Aβ，A2β线性无关.

7.9 【解】（1）因ξ1，ξ2，ξ3 是A的特征向量，假设对应的特征值分别是λ1，λ2，λ3，则有

由等式两端的第一个分量相等，得λ1＝0.

（2）由A是3×3非零矩阵（a11＝1≠0），知r（A）≥1.又由Aξ1＝0，Aξ2＝0，且ξ1，ξ2 线性无关，知r（A）≤1.则r（A）＝1，故ξ1，ξ2 是Ax＝0的基础解系.又因Aξ3＝（－1）ξ3，故A（－ξ3）＝ξ3，Ax＝ξ3 有特解－ξ3，从而Ax＝ξ3 的通解为k1ξ1＋k2ξ2－ξ3，其中k1，k2 是任意常数.

（3）方法一 直接由题设条件定出未知的aij，从而求出A.

因r（A）＝1，故［a21，a22，a23］＝k［1，－2，3］，［a31，a32，a33］＝l［1，－2，3］，即

两端第2个分量，第3个分量分别相等，得

方法二 利用A的相似对角矩阵求A.

因A有三个线性无关的特征向量，取

【注】本题也可先求出A，再求方程组Ax＝ξ3 的通解.