，1）T.由于方程组的系数矩阵的n-1阶子式所以，方程组的系数矩阵的秩为n-1，从而α0是方程组的一个基础解系.因此λ=a+（n-1）b对应的所有特征向量为.设对应特征值λ=a-b的特征向量为y=（y1，y2，…......
2023-10-27
特征值与特征向量的定义
【摘要】：设A是n 阶矩阵，λ是一个数，若存在n维非零列向量ξ，使得则称λ是A 的特征值，ξ是A 的对应于特征值λ的特征向量.由①式，得ξ＝0，因ξ≠0，故齐次方程组x＝0有非零解，于是②式称为A 的特征方程，是未知量λ的n次方程，有n个根，λE－A称为特征矩阵，|λE－A|称为特征多项式.求出λi（i＝1，2，…
设A是n 阶矩阵，λ是一个数，若存在n维非零列向量ξ，使得
则称λ是A 的特征值，ξ是A 的对应于特征值λ的特征向量.
【注】由①式，得
（λE－A）ξ＝0，
因ξ≠0，故齐次方程组（λE－A）x＝0有非零解，于是
②式称为A 的特征方程，是未知量λ的n次方程，有n个根（重根按照重数计），λE－A称为特征矩阵，|λE－A|称为特征多项式.求出λi（i＝1，2，…，n）后，代回（λE－A）x＝0，得（λiE－A）x＝0，求解此方程组，得出的非零解均为矩阵A的属于特征值λi 的特征向量.
见例7.1.(www.chuimin.cn)
例7.1 求矩阵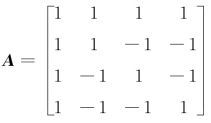
的全部特征值和特征向量.
得特征值λ1＝λ2＝λ3＝2，λ4＝－2.
当λ1＝λ2＝λ3＝2时，由（2E－A）x＝0，即
解得基础解系为ξ1＝［1，1，0，0］T，ξ2＝［1，0，1，0］T，ξ3＝［1，0，0，1］T，故对应于λ1＝λ2＝λ3＝2的全部特征向量为k1ξ1＋k2ξ2＋k3ξ3，其中k1，k2，k3 是不全为零的任意常数.
当λ4＝－2时，由（－2E－A）x＝0，即
解得基础解系为ξ4＝［1，－1，－1，－1］T，故对应于λ4＝－2的全部特征向量为k4ξ4，其中k4 是任意非零常数.
有关张宇线性代数9讲的文章
- 详细阅读
-
高等代数：特征值与特征向量的计算详细阅读
，λs是线性变换σ的s个不同的特征值，Ti是属于特征值λi的线性无关的特征向量组成的向量组，则向量组T1∪T2∪…，αiri线性无关，1≤i≤s，并且满足条件σ（αij）=λiαij，1≤i≤s，1≤j≤ri.下面来证明向量组是线性无关的.若有一组组合系数kij使得记向量，1≤i≤s，由于这表明，若αi≠0，则αi是属于特征值λi的特征向量，由定理5.7可知向量组α1，α2，…......
2023-11-22
-
高等代数：计算特征值和特征向量详细阅读
，αr，并扩充为V的一组基α1，α2，…，n），求αTα的特征值.10.1.5. 证明方阵A可逆的充分必要条件是它的特征值均不是零.10.1.6. 若A可逆，证明：A-1的特征值是A的特征值的倒数.10.1.7. 证明：A2的全部特征值是A的特征值的平方.10.1.8. 证明：若λ1，λ2，…，f（λn）是矩阵f的全部特征值.10.1.9. 求出只与自身相似的所有方阵.10.1.10. 证明：A与AT相似.......
2023-11-22
-
土壤水的状态与特征值详细阅读
X1.6.2.1土壤水的存在状态水分进入土壤后，将受到分子力、毛管力和重力的作用，故以不同的形式存在。在分子力的作用下，吸附于土壤颗粒表面的水分称为吸湿水。X1.6.2.2土壤水分常数土壤水分常数是反映土壤水分形态和性质的特征值。植物根系的吸力约为15个大气压，土壤对水分的吸力相当于15个大气压时的土壤含水量，就是凋萎含水量。......
2023-06-21
-
纹理基元编码与特征向量构建详细阅读
在获得输入图像I的纹理基元编码图像之后，为了方便送入分类器进行类别的判断，需要将编码图像转换成一个特征向量，将其作为原始纹理图像的最终特征描述。显然，利用纹理基元编码图像计算出的直方图特征向量，其特征维数和纹理基元字典的规模是相同的，即每个直方条对应纹理基元字典中的一种纹理基元，直方图的数值则体现了纹理基元编码图像中每个纹理基元出现的频率大小。......
2023-06-29
- 详细阅读
-
函数微分的概念与定义详细阅读
【主要内容】1.函数微分的定义设函数y=f（x）在点x0的某个邻域内有定义.如果y在点x0处的增量Δy=f（x0+Δx）-f（x0） （其中，Δx是自变量x在点x0处的增量）可表示为Δy=AΔx+o（Δx）（其中，A与Δx无关，o（Δx）表示Δx→0时比Δx高阶的无穷小），则称y=f（x）在点x0处可微，称Δy的线性主部AΔx为y=f（x）在点x0处的微分，记为dy|x=x0（注意：函数y=f（x......
2023-10-27
-
概念定义与诠释详细阅读
[1]本文所阐释的服装流行是指“服装的文化倾向，通过具体服装款式的普及、风行一时而形成潮流。这种流行倾向一旦确定，就会在一定的范围内被较多的人所接受。”本文所阐释的文化具有广义和狭义双重含义。文化影响力产生的前提是文化的被感知和被认可。文化影响力产生的表现是文化的凝聚、鼓舞、感召、推动作用。文化影响力可通过文化关联事物的作用力得到壮大、提升。......
2023-06-22
相关推荐