线性代数讲义：求极大线性无关组及相关问题

2023-11-21 理论教育版权反馈

【摘要】：，αn.初等行变换不改变列向量组的线性相关性.求此极大线性无关组.①构造A＝［α1，α2，…并在此时将向量α＝［4，1，6，10］T用α1，α2，α3，α4 线性表示；p为何值时，该向量组线性相关？

给出向量组α1，α2，…，αn.

（1）初等行变换不改变列向量组的线性相关性.

（2）求此极大线性无关组.

①构造A＝［α1，α2，…，αn］.

②

③算出台阶数r，按列找出一个秩为r的子矩阵即可.

见例6.4.

例6.1 已知α1＝［1，－1，1］T，α2＝［1，a，－1］T，α3＝［a，1，2］T，β＝［4，a2，－4］T，若β可由α1，α2，α3线性表示，且表示法不唯一.

（1）求a的值；

（2）求β的表达式.

【解】设x1α1＋x2α2＋x3α3＝β，即

（1）由题设，知r（A）＝r（［A，β］）＜3，从而a＝4.

（2）结合（1），有

方程组（*）的通解为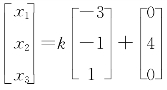 pagenumber_ebook=119,pagenumber_book=111 ，k为任意常数.所以

β＝－3kα1＋（4－k）α2＋kα3，k为任意常数.(www.chuimin.cn)

例6.2 设3维向量 pagenumber_ebook=119,pagenumber_book=111 .又设A是3阶矩阵，满足Aα1＝α2，Aα2＝α3，Aα3＝α4，求Aα4.

【解】因α1，α2，α3，α4 均为具体型（分量均给出），故先寻找它们的关系.设x1α1＋x2α2＋x3α3＝α4，于是

此方程组有唯一解，解得x1＝2，x2＝－1，x3＝1，得α4＝2α1－α2＋α3，则

例6.3 已知3维列向量组α1，α2，α3 线性无关，则向量组α1－α2，α2－kα3，α3－α1 也线性无关的充要条件是________.

【解】应填k≠1.

因α1，α2，α3 线性无关，故α1－α2，α2－kα3，α3－α1 线性无关的充要条件是

例6.4 设向量组

α1＝［1，1，1，3］T，α2＝［－1，－3，5，1］T，α3＝［3，2，－1，p＋2］T，α4＝［－2，－6，10，p］T.

（1）p为何值时，该向量组线性无关？并在此时将向量α＝［4，1，6，10］T用α1，α2，α3，α4 线性表示；

（2）p为何值时，该向量组线性相关？并在此时求出它的秩和一个极大线性无关组.

【解】对矩阵［α1，α2，α3，α4，α］作初等行变换，有

（1）当p≠2时，向量组α1，α2，α3，α4 线性无关.此时设α＝x1α1＋x2α2＋x3α3＋x4α4，解得

（2）当p＝2时，向量组α1，α2，α3，α4 线性相关.此时，向量组的秩等于3.α1，α2，α3（或α1，α3，α4）为其一个极大线性无关组.

【注】对列向量组α1，α2，α3，α4 作初等行变换得到β1，β2，β3，β4，则向量组α1，α2，α3，α4 与向量组β1，β2，β3，β4 有着相同的对应关系，即如果β1，β2，β3 是β1，β2，β3，β4 的极大线性无关组，则α1，α2，α3 是α1，α2，α3，α4 的极大线性无关组，且α4 由α1，α2，α3 线性表示的系数与β4 由β1，β2，β3 线性表示的系数相同.

线性代数讲义：求极大线性无关组及相关问题

相关推荐