（1）定义（Eij，Eij（k），Ei（k））.①初等变换.（ⅰ）一个非零常数乘矩阵的某一行（列）.（ⅱ）互换矩阵中某两行（列）的位置.（ⅲ）将矩阵的某一行（列）的k倍加到另一行（列）.以上三种变换称为矩阵的初等行（列）变换，且分别称为倍乘、互换、倍加初等行（列）变换.②初等矩阵.由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵.以3阶矩阵为例，并随之给出定义.（ⅰ）E2（k）＝，E 的第2行（或......
2023-11-21
张宇线性代数9讲：求解A矩阵
【摘要】：，αm，βT线性无关.例5.16 已知齐次线性方程组A2×4x＝0的基础解系为ξ1＝［1，－1，3，2］T，ξ2＝［2，1，1，－3］T，则A＝________.应填，其中k1，l1，k2，l2 是不全为零的常数，且k1l2≠k2l1.由题设条件知，Aξ1＝0，Aξ2＝0，即两边转置，得作齐次线性方程组对系数矩阵作初等行变换，有取y2＝0，y3＝k，得，则解向量为取y2＝l，y3＝0，得，则解向量为其中k1，l1，k2，l2 是不全为零的常数，且k1l2≠k2l1.
若齐次线性方程组
有解β＝［b1，b2，…，bn］T，即
ai1b1＋ai2b2＋…＋ainbn＝0（i＝1，2，…，m）.
记αi＝［ai1，ai2，…，ain］（i＝1，2，…，m），上式即为
故系数矩阵A的行向量与Ax＝0的解向量正交，将式（*）两边转置，得
βTαTi＝0，
即将解向量的转置作为齐次线性方程组的行向量时，A的行向量的转置即是该方程组的解向量.
以上论述说明A的行向量与Ax＝0的解向量可以进行“角色互换”.读者在应对某些综合性问题时，应充分利用这一特点.
见例5.15，例5.16.
例5.11 设A是n 阶矩阵，α是n 维列向量.若
，则线性方程组（）.
（A）Ax＝α必有无穷多解（B）Ax＝α 必有唯一解
（C）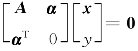
仅有零解（D）
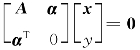必有非零解
【解】应选（D）.
由于
，故r（A）＝r（［A，α］），于是Ax＝α必有解，但具体是只有唯一解还是有无穷多解无法确定.又
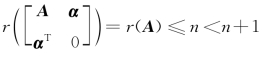，故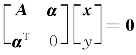
必有非零解，选项（D）正确.
例5.12 设α1，α2，…，αs 为线性方程组Ax＝0的一个基础解系，且
β1＝t1α1＋t2α2，β2＝t1α2＋t2α3，…，βs＝t1αs＋t2α1，
其中t1，t2 为实常数，问t1，t2 满足什么关系时，β1，β2，…，βs 也为Ax＝0的一个基础解系？
【解】①βi（i＝1，2，…，s）是方程组的解.因Aαj＝0，j＝1，2，…，s，故
Aβi＝A（t1αi＋t2αi＋1）＝0（记αs＋1＝α1），i＝1，2，…，s.
②要保证β1，β2，…，βs 线性无关.
方法一 设k1β1＋k2β2＋…＋ksβs＝0，即
k1（t1α1＋t2α2）＋k2（t1α2＋t2α3）＋…＋ks（t1αs＋t2α1）＝0，
整理得
（k1t1＋kst2）α1＋（k2t1＋k1t2）α2＋…＋（kst1＋ks－1t2）αs＝0.
由于α1，α2，…，αs 线性无关，因此有
以k1，k2，…，ks 为未知数，则其系数行列式为
所以，当ts1＋（－1）s＋1ts2≠0（即s为偶数时，t1≠±t2；s为奇数时，t1≠－t2）时，方程组（*）有唯一零解，从而β1，β2，…，βs 线性无关.
方法二 由题设条件，知
当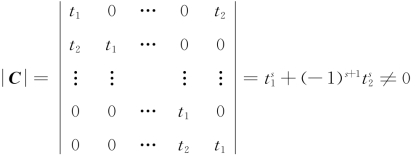
时，C可逆，且
［α1，α2，…，αs］＝［β1，β2，…，βs］C－1，
故当ts1＋（－1）s＋1ts2≠0（即s为偶数时，t1≠±t2；s为奇数时，t1≠－t2）时，α1，α2，…，αs 和β1，β2，…，βs 等价⇒r（α1，α2，…，αs）＝r（β1，β2，…，βs）＝s，于是β1，β2，…，βs 线性无关.
③向量组β1，β2，…，βs 中向量个数也为s.
由①，②，③可知，当s为偶数，且t1≠±t2 时，当s为奇数，且t1≠－t2 时，向量组β1，β2，…，βs 也是方程组Ax＝0的一个基础解系.(www.chuimin.cn)
例5.13 已知n阶矩阵A的各行元素之和均为零，且r（A）＝n－1，则线性方程组Ax＝0的通解是________.
【解】应填k［1，1，…，1］T，其中k为任意常数.
由r（A）＝n－1知Ax＝0的基础解系由n－（n－1）＝1个非零向量组成.A的各行元素之和均为零，
即 ai1＋ai2＋…＋ain＝0，i＝1，2，…，n，
也就是 ai1·1＋ai2·1＋…＋ain·1＝0，i＝1，2，…，n，
即ξ＝［1，1，…，1］T是Ax＝0的非零解，于是方程组Ax＝0的通解为k［1，1，…，1］T，其中k为任意常数.
例5.14 设α1，α2，α3 是四元非齐次线性方程组Ax＝b的三个解向量，且k是任意常数，则方程组Ax＝b的通解是（）.
r（A）＝3，α1＝［1，2，3，4］T，α2＋α3＝［0，1，2，3］T，
【解】应选（C）.
方程组对应的齐次方程组有解2α1－（α2＋α3）＝［2，3，4，5］T，而对应齐次方程组的基础解系仅有4－3＝1个向量，故选（C）.
例5.15 设αi＝［ai1，ai2，…，ain］（i＝1，2，…，m）为齐次线性方程组
的系数矩阵的行向量，已知方程组①有非零解β＝［b1，b2，…，bn］T，且行向量组的秩r（α1，α2，…，αm）＝m.证明：向量组α1，α2，…，αm，βT线性无关.
【分析】β是方程组①的非零解，即有
ai1b1＋ai2b2＋…＋ainbn＝0（i＝1，2，…，m），
表示成向量形式是 αiβ＝0（i＝1，2，…，m），即β与αi（i＝1，2，…，m）正交，利用正交性证明向量组线性无关.
【证】利用线性无关的定义.
设存在数k0，k1，k2，…，km，使得
式②两端右乘β，得
因β是方程组①的非零解，故有αiβ＝0（i＝1，2，…，m），且βTβ≠0，从而由式③得
k0βTβ＝0⇒k0＝0.
将k0＝0代入式②，得
k1α1＋k2α2＋…＋kmαm＝0.
由于r（α1，α2，…，αm）＝m，即α1，α2，…，αm 线性无关，故k1＝k2＝…＝km＝0，又k0＝0，故向量组α1，α2，…，αm，βT线性无关.
例5.16 已知齐次线性方程组A2×4x＝0的基础解系为
ξ1＝［1，－1，3，2］T，ξ2＝［2，1，1，－3］T，
则A＝________.
【解】应填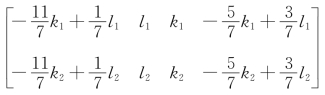
，其中k1，l1，k2，l2 是不全为零的常数，且k1l2≠k2l1.
由题设条件知，Aξ1＝0，Aξ2＝0，即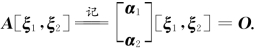
两边转置，得
作齐次线性方程组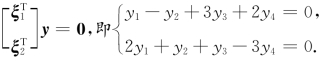
对系数矩阵作初等行变换，有
取y2＝0，y3＝k，得
，则解向量为
取y2＝l，y3＝0，得
，则解向量为
其中k1，l1，k2，l2 是不全为零的常数，且k1l2≠k2l1（因α1，α2 线性无关）.
有关张宇线性代数9讲的文章
- 详细阅读
- 详细阅读
-
张宇线性代数9讲：A的相似对角化详细阅读
设n阶矩阵A，若存在n阶可逆矩阵P，使得P－1AP＝Λ，其中Λ 是对角矩阵，则称A可相似对角化，记A～Λ，称Λ 是A 的相似标准形.于是可知，若A可相似对角化，即P－1AP＝Λ，其中P可逆，等式两边同时左乘P，有AP＝PΛ，记由P可逆，则ξ1，ξ2，…＝λn＝0，A的特征值全是零.若A能与对角矩阵Λ 相似，则Λ 的主对角线元素为A......
2023-11-21
-
线性代数9讲-实对称矩阵与正交矩阵详细阅读
（1）若A为实对称矩阵，则①特征值均为实数，特征向量均为实向量.②不同特征值对应的特征向量正交.（即λ1≠λ2ξ1⊥ξ2（ξ1，ξ2）＝0，建方程）③可用正交矩阵相似对角化.（即存在正交矩阵P，使P－1AP＝PTAP＝Λ）见例8.12至例8.15.（2）若A为正交矩阵，则ATA＝EA－1＝ATA由规范正交基组成AT是正交矩阵A－1是正交矩阵A*是正交矩阵－A是正交矩阵.（3）若A，B为同阶正交矩阵......
2023-11-21
- 详细阅读
-
秩的公式见第4讲-张宇线性代数9讲详细阅读
，tn－11］，α2＝［1，t2，…，tn－1r］，其中t1，t2，…＋kr，k1t1＋k2t2＋…，tr－1r］.由上述①的证明知β1，β2，…，tn－1r］，分别是向量β1，β2，…，1，－1］T，其中k是任意常数.......
2023-11-21
-
张宇线性代数9讲中的三考法：解析，矩阵乘法规详细阅读
，0］，则Aβi＝0（i＝1，2，…，s）是Ax＝0的解.设矩阵Am×n，Bn×s，若AB＝C，则C是m×s矩阵.将B，C按行分块，有则γi＝ai1β1＋ai2β2＋…，m），故C的行向量是B 的行向量的线性组合.类似地，若A，C按列分块，则有则ξi＝α1b1i＋α2b2i＋…......
2023-11-21
-
张宇线性代数9讲：判断相关性的7大定理详细阅读
，αn（n≥2）线性相关，则存在n 个不全为零的数k1，k2，…，αn 线性表示的表示法唯一.定理3 如果向量组β1，β2，…，αn 线性相关有非零解.仿定理4的研究方法，便有下面所给的定理5.定理5 向量β可由向量组α1，α2，…，αm 线性无关，则其任一部分向量组也线性无关.总之，向量组部分线性相关，则整体也线性相关；整体线性无关，则任一部分也线性无关.定理7 如果一组n维向量α1，α2，…......
2023-11-21
相关推荐