线性代数求解方程组的公共解与同解问题

2023-11-21 理论教育版权反馈

【摘要】：求两个方程组的公共解.①齐次线性方程组Am×nx＝0和Bm×nx＝0的公共解是满足方程组的解，即联立求解.同理，可求Ax＝α与Bx＝β的公共解.这里对读者的计算能力提出较高要求，但理论上没有什么难点.②求出Am×nx＝0的通解k1ξ1＋k2ξ2＋…

（1）求两个方程组的公共解.

①齐次线性方程组Am×nx＝0和Bm×nx＝0的公共解是满足方程组 pagenumber_ebook=89,pagenumber_book=81 的解，即联立求解.同理，

可求Ax＝α与Bx＝β的公共解.这里对读者的计算能力提出较高要求，但理论上没有什么难点.

②求出Am×nx＝0的通解k1ξ1＋k2ξ2＋…＋ksξs，代入Bm×nx＝0，求出ki（i＝1，2，…，s）之间的关系，代回Am×nx＝0的通解，即得公共解.

见例5.8方法一.

③若给出Am×nx＝0的基础解系ξ1，ξ2，…，ξs 与Bm×nx＝0的基础解系η1，η2，…，ηt，则公共解

解此式，求出ki 或lj，i＝1，2，…，s；j＝1，2，…，t，即可写出γ.

见例5.8方法二.

（2）同解方程组.

若两个方程组Am×nx＝0和Bs×nx＝0有完全相同的解，则称为同解方程组.

于是，Ax＝0，Bx＝0是同解方程组

⇔Ax＝0的解满足Bx＝0，且Bx＝0的解满足Ax＝0（互相把解代入求出结果即可）

⇔r（A）＝r（B），且Ax＝0的解满足Bx＝0（或Bx＝0的解满足Ax＝0）

⇔r（A）＝r（B）＝ pagenumber_ebook=89,pagenumber_book=81 （三秩相同较方便）.

见例5.9，例5.10.

例5.8 设四元齐次线性方程组（Ⅰ）为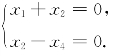 pagenumber_ebook=89,pagenumber_book=81 又已知某齐次线性方程组（Ⅱ）的通解为k1［0，1，1，0］T＋k2［－1，2，2，1］T.

（1）求线性方程组（Ⅰ）的基础解系；

（2）线性方程组（Ⅰ）和（Ⅱ）是否有非零公共解？若有，则求出所有的非零公共解，若没有，则说明理由.

【解】（1）由已知，方程组（Ⅰ）的系数矩阵为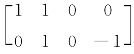 pagenumber_ebook=90,pagenumber_book=82 ，故（Ⅰ）的基础解系可取为［0，0，1，0］T，［－1，1，0，1］T.

（2）有非零公共解.

方法一将方程组（Ⅱ）的通解代入方程组（Ⅰ），有

解得k1＝－k2.当k1＝－k2≠0时，则向量

满足方程组（Ⅰ）（显然是（Ⅱ）的解）.故方程组（Ⅰ）与（Ⅱ）有非零公共解，所有非零公共解是

k［－1，1，1，1］T（k为任意非零常数）.

方法二方程组（Ⅰ）的通解为l1［0，0，1，0］T＋l2［－1，1，0，1］T，方程组（Ⅱ）的通解为k1［0，1，1，0］T＋k2［－1，2，2，1］T，则公共解应满足

故l1＝l2＝－k1＝k2，因此方程组（Ⅰ），（Ⅱ）的公共解为

l1［0，0，1，0］T＋l2［－1，1，0，1］T＝l1［－1，1，1，1］T.

故方程组（Ⅰ），（Ⅱ）有非零公共解，所有非零公共解为

k［－1，1，1，1］T（k为任意非零常数）.(www.chuimin.cn)

例5.9 已知A为m×n矩阵，x＝［x1，x2，…，xn］T，e＝［1，1，…，1］T为n维列向量，若Ay＝e有解，则对于方程组（Ⅰ）ATx＝0与（Ⅱ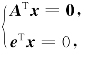） pagenumber_ebook=90,pagenumber_book=82 下列结论正确的是（）.

（A）（Ⅰ）的解全是（Ⅱ）的解，（Ⅱ）的解不全是（Ⅰ）的解

（B）（Ⅱ）的解全是（Ⅰ）的解，（Ⅰ）的解不全是（Ⅱ）的解

（C）（Ⅰ）与（Ⅱ）只有零公共解

（D）（Ⅰ）与（Ⅱ）同解

【解】应选（D）.

由于Ay＝e有解，取y0 满足此方程，即Ay0＝e.

若γ是（Ⅰ）的任一解，则ATγ＝0.又eTγ＝（Ay0）Tγ＝yT0ATγ＝yT0·0＝0，于是γ满足eTx＝0，γ也满足ATx＝0，即γ满足（Ⅱ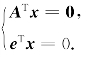） pagenumber_ebook=90,pagenumber_book=82

若η是（Ⅱ）的任一解，显然，它是（Ⅰ）的解.

综上所述，（Ⅰ）与（Ⅱ）同解.选（D）.

例5.10 已知方程组

问参数a，b，c满足什么条件时，方程组（Ⅰ）和（Ⅱ）是同解方程组.

【解】方法一先求方程组（Ⅰ）Ax＝0的通解，（Ⅰ）的系数矩阵

已是阶梯形，求得基础解系为ξ1＝［－1，2，－1，1，0］T，ξ2＝［－1，－2，1，0，1］T，则方程组（Ⅰ）的通解为

方程组（Ⅰ），（Ⅱ）是同解方程组，将ξ1＝［－1，2，－1，1，0］T代入（Ⅱ）的第1，2个方程，

－2（－1）＋2＋a（－1）－5＝0，得a＝－1.

－1＋2－（－1）＋b＝0，得b＝－2.

显然ξ1 也满足（Ⅱ）的第3个方程.

将ξ2＝［－1，－2，1，0，1］T代入（Ⅱ）的第3个方程，3（－1）＋（－2）＋1＋c＝0，得c＝4.

显然，当a＝－1，b＝－2时，ξ2 也满足（Ⅱ）的第1，2个方程.

故知当a＝－1，b＝－2，c＝4时，由解的性质知方程组（Ⅰ）的解全部是（Ⅱ）的解.

反之，当a＝－1，b＝－2，c＝4时，方程组（Ⅱ）的系数矩阵的秩为

（Ⅱ）的未知量个数n＝5，（Ⅱ）的基础解系由两个线性无关解组成，已验算（Ⅰ）的解全部是（Ⅱ）的解，故（Ⅱ）的解也全部是（Ⅰ）的解，方程组（Ⅰ），（Ⅱ）是同解方程组.

方法二（Ⅰ），（Ⅱ）是同解方程组，（Ⅰ）和（Ⅱ）的系数行向量组是等价向量组，可以相互表出，记（Ⅰ）的三个行向量分别为α1，α2，α3，（Ⅱ）的三个行向量分别为β1，β2，β3，将［αT1，αT2，αT3┊βT1，βT2，βT3］作初等行变换，化成阶梯形，得

当取a＝－1，b＝－2，c＝4时，β1，β2，β3 可由α1，α2，α3 线性表出.

反之，当a＝－1，b＝－2，c＝4时，因

可知α1，α2，α3 也可由β1，β2，β3 线性表出.故当a＝－1，b＝－2，c＝4时，方程组（Ⅰ），（Ⅱ）是同解方程组.

线性代数求解方程组的公共解与同解问题

相关推荐