解线性方程组|张宇线代9讲|齐次与非齐次方程组|克拉默法则

2023-11-21 理论教育版权反馈

【摘要】：齐次线性方程组.对于齐次线性方程组记则齐次线性方程组①可写成矩阵方程①解向量及其性质.如果x1＝λ1，x2＝λ2，…，ξn－r 为方程组①的一个基础解系.见例5.3.非齐次线性方程组.①克拉默法则.若线性方程组的系数行列式，则该方程组有唯一解其中Dj（j＝1，2，…

（1）齐次线性方程组.

对于齐次线性方程组

记

则齐次线性方程组①可写成矩阵方程

①解向量及其性质.

如果x1＝λ1，x2＝λ2，…，xn＝λn 为齐次线性方程组①的解，则

称为方程组①的解向量，它就是矩阵方程②的解.

解向量有如下性质：

（ⅰ）若ξ1，ξ2 是②的解，则x＝ξ1＋ξ2 也是②的解；

（ⅱ）若x＝ξ是②的解，k∈R，则x＝kξ 也是②的解.

②基础解系.

设ξ1，ξ2，…，ξs 是方程组①的一组解向量，如果

（ⅰ）ξ1，ξ2，…，ξs 线性无关；

（ⅱ）方程组①的任一解向量均可由ξ1，ξ2，…，ξs 线性表示，即s＝n－r（A）.

则称ξ1，ξ2，…，ξs 是方程组①的一个基础解系.

【注】基础解系应满足3条：（1）是解；（2）线性无关；（3）s＝n－r（A）.

③齐次线性方程组有非零解的充要条件及通解.

齐次线性方程组①有非零解的充要条件是r（A）＜n，此时它的通解为

x＝k1ξ1＋k2ξ2＋…＋kn－rξn－r，

其中r＝r（A），k1，k2，…，kn－r 为任意常数，ξ1，ξ2，…，ξn－r 为方程组①的一个基础解系.

见例5.3（1）.

（2）非齐次线性方程组.

①克拉默法则.

若线性方程组

的系数行列式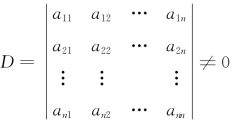 pagenumber_ebook=81,pagenumber_book=73 ，则该方程组有唯一解

其中Dj（j＝1，2，…，n）是将D 中第j列元素换成b1，b2，…，bn 所构成的行列式，即

特别地，当bi＝0（i＝1，2，…，n）时，如果D≠0，则方程组③只有零解xi＝0（i＝1，2，…，n）.反之，当bi＝0（i＝1，2，…，n）时，如果方程组③有非零解，则D＝0.

见例5.1，例5.2.

②几个相关问题的等价性.

记

则非齐次线性方程组

可写成矩阵方程

及

以下4种说法是等价的.

（ⅰ）方程组④有解；

（ⅱ）向量b能由向量组α1，α2，…，αn 线性表示；

（ⅲ）向量组α1，α2，…，αn 与向量组α1，α2，…，αn，b等价；(www.chuimin.cn)

（ⅳ）方程组④的系数矩阵A＝［α1，α2，…，αn］与其增广矩阵［A┊b］＝［α1，…，αn┊b］的秩相等.

③非齐次线性方程组有解的充要条件.

非齐次线性方程组④有解的充要条件是r（A）＝r（［A，b］）.确切地说，当r（A）＝r（［A，b］）＝n时，方程组④有唯一解；当r（A）＝r（［A，b］）＜n时，方程组④有无穷多解；当r（A）≠r（［A，b］）时，方程组④无解.

相应地，当r（A）＝r（［A，b］）＝n时，向量b能由向量组α1，α2，…，αn线性表示，且表达式是唯一的；当r（A）＝r（［A，b］）＜n时，向量b能由向量组α1，α2，…，αn线性表示，但表达式不唯一；当r（A）≠r（［A，b］）时，向量b不能由向量组α1，α2，…，αn 线性表示.

④非齐次线性方程组解的结构.

（ⅰ）方程组的解向量.

如果x1＝λ1，x2＝λ2，…，xn＝λn 为方程组④的解，则

称为方程组④的解向量，它就是矩阵方程⑤的解.

（ⅱ）解向量的性质.

若x＝η1，x＝η2 都是方程⑤的解，则x＝η1－η2 是相应的齐次线性方程组②的解.

（ⅲ）非齐次线性方程组解的结构定理.

若ξ1，ξ2，…，ξn－r为方程⑤相应的齐次线性方程组②的基础解系，η*为方程⑤的某一个特解，则方程⑤的通解为

x＝η*＋k1ξ1＋k2ξ2＋…＋kn－rξn－r，

其中r＝r（A），k1，k2，…，kn－r 为任意常数.

【注】与方程组④对应的齐次方程组①称为方程组④的导出组.故上述结论可简述：非齐次线性方程组的通解等于它的一个特解与其导出组的通解之和.

见例5.3（2）.

例5.1 求解线性方程组：

【分析】对于方程个数与未知数个数相等的线性方程组，若其系数行列式不为零，则可用克拉默法则求解.

【解】因为方程组的系数行列式

所以由克拉默法则知原方程组有唯一解.又

用同样的方法可以计算

所以原方程组的唯一解是

例5.2 讨论当λ取何值时下述线性方程组有唯一零解：

【解】由于方程组的系数行列式

故由克拉默法则知，当（λ＋2）（λ－1）2≠0，即λ≠－2且λ≠1时，方程组有唯一零解.

例5.3 求解下列线性方程组：

【分析】利用矩阵的初等行变换求解齐次或非齐次线性方程组，其基本思想是利用初等行变换将所给方程组化为与之等价的阶梯形方程组，进而求解.

【解】（1）对方程组的系数矩阵进行初等行变换，有

由此知r（A）＝2＜4，故原方程组有无穷多解，且有同解方程组

令x2＝k1，x4＝k2，则原方程组的通解为

亦即x＝k1ξ1＋k2ξ2（k1，k2 为任意常数），其中ξ1＝［1，1，0，0］T，ξ2＝［－2，0，－3，1］T为原方程组的一个基础解系.

（2）对增广矩阵进行初等行变换，有

由于r（B）＝r（A）＝3＜4，故方程组有无穷多解，且有同解方程组

从而原方程组的通解为

或x＝η＋x3ξ，即x＝η＋kξ（k为任意常数），其中η＝［－1，1，0，－2］T，ξ＝［－3，－5，1，0］T分别为原方程组的一个特解与相应齐次方程组的一个基础解系.

解线性方程组|张宇线代9讲|齐次与非齐次方程组|克拉默法则

相关推荐