【摘要】:,0],则Aβi=0(i=1,2,…,s)是Ax=0的解.设矩阵Am×n,Bn×s,若AB=C,则C是m×s矩阵.将B,C按行分块,有则γi=ai1β1+ai2β2+…,m),故C的行向量是B 的行向量的线性组合.类似地,若A,C按列分块,则有则ξi=α1b1i+α2b2i+…
(1)用阶梯数(用定义).
见例4.1.
(2)用公式.
见例4.2至例4.7.
例4.1已知 ,则以下(a,b)的取值能使得A与B等价的是().
,则以下(a,b)的取值能使得A与B等价的是().
(A)(3,-2) (B)(-3,-1) (C)(3,1) (D)(-3,1)
【解】应选(D).
用初等变换将A,B分别化为阶梯形矩阵,阶梯数即为矩阵的秩.
将A的第4行乘以(-1)分别加到第1,2,3行,有
将A1 的第2,3,4列加到第1列,有
将A2 的第1,2,3行都乘以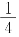 加到第4行,有
加到第4行,有
交换A3 的第1,3行,有
阶梯数为3,故r(A)=3.
又
由于A与B 等价,故r(B)=r(A)=3.只有(D)中的a=-3,b=1,使得
阶梯数为3,故r(B)=3,故选(D).
例4.2 设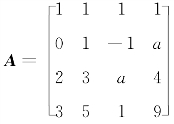 ,若r(A*)=1,则a=().
,若r(A*)=1,则a=().
(A)1 (B)3 (C)1或3 (D)无法确定
【解】应选(C).
由r(A*)=1得r(A)=3,则|A|=0,即
得a=1或a=3,经验算,此时均满足r(A)=3,故选(C).
例4.3 设A是5阶方阵,且A2=O,则r(A*)=________.
【解】应填0.
因
A2=AA=O,r(A)+r(A)≤5,r(A)≤2,
从而
A*=O,r(A*)=0.
例4.4 已知r(A3×3)=2,r(AB)=1,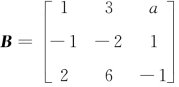 ,则a=________.
,则a=________.
【解】应填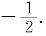
由题意知,r(AB)<r(A),若r(B)=3,则r(AB)=2,与已知矛盾,故r(B)<3,则
例4.5 设 ,若Ax=0的基础解系中只有1个解向量,则a=________.
,若Ax=0的基础解系中只有1个解向量,则a=________.
【解】应填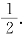
【注】亦可命制成“Ax=0的任一解均可由一个3维非零解向量ξ线性表示”,答案不变.
例4.6 设A是3阶矩阵,β1,β2,β3 是互不相同的3维列向量,且都不是方程组Ax=0的解,记B=[β1,β2,β3],且满足r(AB)<r(A),r(AB)<r(B),则r(AB)=().
(A)0(B)1(C)2(D)3
【解】应选(B).
已知βi(i=1,2,3)都不是Ax=0的解,即AB≠O,r(AB)≥1.又r(AB)<r(A),则矩阵B不可逆(若B可逆,则r(AB)=r(A),这和r(AB)<r(A)矛盾),r(B)≤2,从而r(AB)<r(B)≤2,即r(AB)≤1,从而有r(AB)=1.
【注】B可逆⇒r(AB)=r(A).但反之,r(AB)=r(A)⇒B可逆,不一定成立.如A=O,则有r(AB)=r(A),B可任意.
例4.7 设A,B为n 阶矩阵,记r(X)为矩阵X 的秩,[X Y]表示分块矩阵,则().
(A)r([A AB])=r(A) (B)r([A BA])=r(A)
(C)r([A B])=max{r(A),r(B)}(D)r([A B])=r([ATBT])
【解】应选(A).
方法一 一方面,A是[A AB]的子矩阵,因此r([A AB])≥r(A).
另一方面,[A AB]是A 与[E B]的乘积,即[A AB]=A[E B],因此r([A AB])≤r(A),故r([A AB])=r(A).选(A).
方法二 设C=AB,则C的列向量可由A 的列向量线性表示,故r([A AB])=r([A C])=r(A),选(A).
对于选项(B),(C),(D)可举出反例.
取 则
则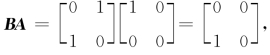 从而r(A)=1,r([A BA])=
从而r(A)=1,r([A BA])= ,有r(A)≠r([A BA]),知选项(B)错误;
,有r(A)≠r([A BA]),知选项(B)错误;
取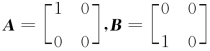 ,则r(A)=r(B)=1,而
,则r(A)=r(B)=1,而
知选项(C)错误;
取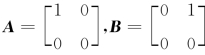 ,则
,则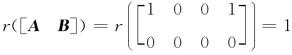 ,而
,而
知选项(D)也错误.
【注】(1)若Am×nBn×s=O,将B,O按列分块,有
AB=A[β1,β2,…,βs]=[Aβ1,Aβ2,…,Aβs]=[0,0,…,0],
则Aβi=0(i=1,2,…,s),故βi(i=1,2,…,s)是Ax=0的解.
(2)设矩阵Am×n,Bn×s,若AB=C,则C是m×s矩阵.将B,C按行分块,有
则γi=ai1β1+ai2β2+…+ainβn(i=1,2,…,m),故C的行向量是B 的行向量的线性组合.类似地,若A,C按列分块,则有
则ξi=α1b1i+α2b2i+…+αnbni(i=1,2,…,s),故C的列向量是A 的列向量的线性组合.(www.chuimin.cn)
4.1 设A,B,C,D是四个4阶矩阵,其中A,D是非零矩阵,B,C是可逆矩阵,且满足ABCD=O,若r(A)+r(B)+r(C)+r(D)=r,则r的取值范围是().
(A)r<10 (B)10≤r≤12 (C)12<r<16 (D)r≥16
4.2 设A是4×3矩阵,B是3×4的非零矩阵,满足AB=O,其中
则必有().
(A)当t=3时,r(B)=1 (B)当t≠3时,r(B)=1
(C)当t=3时,r(B)=2 (D)当t≠3时,r(B)=2
4.3 设A是3阶非零矩阵,满足A2=A,且A≠E,则必有().
(A)r(A)=1 (B)r(A-E)=2
(C)[r(A)-1][r(A-E)-2]=0(D)[r(A)-1][r(A-E)-1]=0
4.4 设A,B,C均是3阶方阵,满足AB=C,其中
则必有().
(A)a=-1时,r(A)=1 (B)a=-1时,r(A)=2
(C)a≠-1时,r(A)=1(D)a≠-1时,r(A)=2
4.5 设A,B是3阶矩阵,A是非零矩阵,且满足AB=O,其中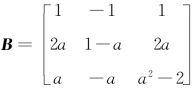 ,则().
,则().
(A)a=-1时,必有r(A)=1 (B)a=2时,必有r(A)=2
(C)a=-1时,必有r(A)=2(D)a=2时,必有r(A)=1
4.6 设A,B均是n 阶矩阵,满足AB=A+B,则r(AB-BA+A-E)=________.
4.1 【解】应选(B).
因A≠O,D≠O,故r(A)≥1,r(D)≥1,r(A)+r(D)≥2.由|B|≠0,|C|≠0,故r(B)=4,r(C)=4.
从而有 r(A)+r(B)+r(C)+r(D)≥10.
又由ABCD=O,其中B,C可逆,得r(AB)+r(CD)=r(A)+r(D)≤4.从而有
r(A)+r(B)+r(C)+r(D)≤12.
故 10≤r≤12.
4.2 【解】应选(B).
由题设AB=O,知r(A)+r(B)≤3(3是A的列数或B 的行数).
因B是非零矩阵,有r(B)≥1,从而有1≤r(B)≤3-r(A).
又
当t=3时,r(A)=1,故1≤r(B)≤2.r(B)=1或r(B)=2,故(A),(C)不成立.
当t≠3时,r(A)=2,故1≤r(B)≤1,故r(B)=1.
故应选(B).
4.3 【解】应选(D).
已知A是3阶非零矩阵,则A≠O,r(A)≥1.
A≠E,A-E≠O,r(A-E)≥1,
因A2=A,由本讲中“二(11)”的结论,得r(A)+r(A-E)=3.
故矩阵A和A-E的秩r(A)和r(A-E)一个是1,另一个是2,至少有一个的秩为1,但不知道哪一个的秩为1,故(A),(B),(C)均是错误的,正确选项是(D).
4.4 【解】应选(C).
显然r(C)=1.因
当a≠-1时,有r(B)=3.B可逆,因AB=C,故r(A)=r(AB)=r(C)=1.故应选(C).
因(C)成立,显然(D)不能成立.(A),(B)也不能成立,可举反例如下.
当a=-1时,可取 ,有AB=C,此时r(A)=1.
,有AB=C,此时r(A)=1.
也可取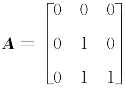 ,也有AB=C,此时r(A)=2.
,也有AB=C,此时r(A)=2.
故(A),(B)均不成立.
4.5 【解】应选(D).
由AB=O,知r(A)+r(B)≤3.又r(A)≥1,故r(B)<3.由已知,有
因此a=-1或者a=2.
当a=-1时,r(B)=1,则r(A)=1或r(A)=2.故(A),(C)不成立.
当a=2时,r(B)=2,必有r(A)=1.(D)成立,(B)不成立,故应选(D).
4.6 【解】应填n.
由题设条件AB=A+B,得
AB-A=A(B-E)=B,
A(B-E)-(B-E)=E,(A-E)(B-E)=E,
从而知A-E 和B-E 是互逆矩阵,且有
(B-E)(A-E)=BA-A-B+E=E,BA=A+B,
从而知AB=BA,且r(A-E)=r(B-E)=n,故
r(AB-BA+A-E)=r(A-E)=n.

 ,则以下(a,b)的取值能使得A与B等价的是().
,则以下(a,b)的取值能使得A与B等价的是().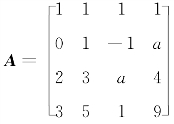 ,若r(A
,若r(A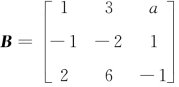 ,则a=________.
,则a=________. ,若Ax=0的基础解系中只有1个解向量,则a=________.
,若Ax=0的基础解系中只有1个解向量,则a=________. 则
则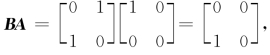 从而r(A)=1,r([A BA])=
从而r(A)=1,r([A BA])= ,有r(A)≠r([A BA]),知选项(B)错误;
,有r(A)≠r([A BA]),知选项(B)错误;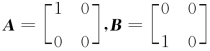 ,则r(A)=r(B)=1,而
,则r(A)=r(B)=1,而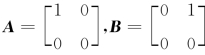 ,则
,则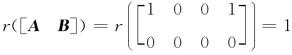 ,而
,而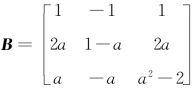 ,则().
,则(). ,有AB=C,此时r(A)=1.
,有AB=C,此时r(A)=1.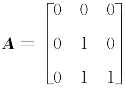 ,也有AB=C,此时r(A)=2.
,也有AB=C,此时r(A)=2.





相关推荐