张宇线性代数9讲：求解线性方程组

（1）若A或B，或A且B 可逆，则分别可得解为X＝A－1B，X＝BA－1，X＝A－1CB－1.

见例3.19，例3.20.

（2）若A不可逆，如AX＝B，则将X 和B 按列分块，得

A［ξ1，ξ2，…，ξn］＝［β1，β2，…，βn］，即Aξi＝βi，i＝1，2，…，n.

求解上述线性方程组，得解ξi，从而得X＝［ξ1，ξ2，…，ξn］.

见例3.21，例3.23.

（3）若无法化成上述几种形式，则应该设未知矩阵为X＝（xij），直接代入方程得到含未知量为xij的线性方程组，求得X 的元素xij，从而求得未知矩阵（即用待定元素法求X）.

见例3.22.

例3.19 设矩阵A的伴随矩阵

已知3AXA－1＝XA－1＋4E，其中E 是4阶单位矩阵.求矩阵X.

【解】由于|A*|＝|A|n－1，有，得.由

3AXA－1＝XA－1＋4E，

方程两边右乘A，得

3AX＝X＋4A，

（3A－E）X＝4A.

左乘A－1，有

由于行列式|3E－2A*|≠0，所以矩阵3E－2A*可逆，故

例3.20 设

其满足＝8A－1B＋16E，求矩阵B.

故，因此有

4A－1BA＝8A－1B＋16E，

A－1B（A－2E）＝4E＝4A－1A，

即 B（A－2E）＝4A.

由|A－2E|＝－4，（A－2E）－1＝，可得

例3.21 设矩阵，且满足AX＋E＝A2＋X，其中E 是3阶单位矩阵，求X.

【解】将矩阵方程进行恒等变形，

知A－E 不可逆.

将X 和（A－E）（A＋E）按列分块，

即 （A－E）ξi＝βi，i＝1，2，3，

解得

故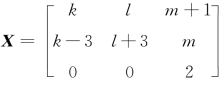，其中k，l，m 是任意常数.

例3.22 设，当a，b为何值时，存在矩阵C，使得AC－CA＝B，并求所有的矩阵C.

【解】设，则

即

对方程组（*）的增广矩阵作初等行变换，有

当a≠－1或b≠0时，方程组（*）无解.

当a＝－1且b＝0时，方程组（*）有解，其同解方程组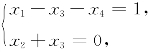为通解为

x＝［1，0，0，0］T＋k1［1，－1，1，0］T＋k2［1，0，0，1］T，

其中k1，k2 为任意常数.故知当且仅当a＝－1，b＝0时，存在满足条件的矩阵C，且

【注】本题矩阵方程无法化简，直接利用待定元素法解线性方程组求解未知矩阵.

例3.23 设矩阵

当a为何值时，方程AX＝B无解、有唯一解、有无穷多解？在有解时，求解此方程.

【解】对矩阵［A┊B］施以初等行变换.

当a≠1且a≠－2时，由于

所以AX＝B有唯一解，且

当a＝1时，由于

所以AX＝B有无穷多解，且

当a＝－2时，由于，所以AX＝B无解.

【注】事实上，有如下定理：

设A为m×n矩阵，B为m×s矩阵，则矩阵方程AX＝B有解的充分必要条件为

r（A）＝r（［A┊B］）.

将X，B按列分块：X＝［x1，x2，…，xs］，B＝［β1，β2，…，βs］.

AX＝B有解⇔A［x1，x2，…，xs］＝［β1，β2，…，βs］有解

⇔Axi＝βi（i＝1，2，…，s）有解

⇔r（A）＝r（［A┊βi］）（i＝1，2，…，s）

⇔r（A）＝r（［A┊β1，β2，…，βs］）

⇔r（A）＝r（［A┊B］）.

上述定理在考研时可直接使用.

3.1 设

（1）计算QP；

（2）设A＝PMQ，计算An.

3.2 设A是n 阶方阵且满足A2＝A，证明：

（A＋E）k＝E＋（2k－1）A，

其中，k是正整数，E 是n 阶单位矩阵.

3.3 设，求An（n为正整数）.

3.4 A是n阶方阵，E是n阶单位矩阵，证明：E－A和（E＋A）*可交换，即证

（E－A）（E＋A）*＝（E＋A）*（E－A）.

3.5 A，B是n 阶方阵且满足AB＝A－B，证明：AB＝BA.

3.6 设A，B是n 阶对称矩阵，证明：

（1）A＋B是对称矩阵；

（2）AB 是对称矩阵的充分必要条件是AB＝BA（即A，B可交换）.

3.7 A是任意n 阶矩阵，证明：

（1）A＋AT是对称矩阵，A－AT是反对称矩阵；

（2）任何n阶方阵都可以表示成一个对称矩阵和一个反对称矩阵的和.

3.8 设A是n阶方阵，E＋A是可逆矩阵，记f（A）＝（E－A）（E＋A）－1.若A满足条件AAT＝E，证明：f（A）是反对称矩阵.

3.9 证明：A是n 阶方阵，对于任意x＝［a1，a2，…，an］T，有xTAx＝0的充分必要条件是A是反对称矩阵.

3.10 设A为n 阶可逆矩阵，α为n 维列向量，b为常数.记分块矩阵

其中A*是矩阵A的伴随矩阵，E 为n 阶单位矩阵.

（1）计算并化简PQ；

（2）证明：矩阵Q可逆的充分必要条件是αTA－1α≠b.

3.11 设A为实矩阵，B＝AAT，且，则A＝________.

3.12 设A，B为n 阶矩阵，且满足AB＋BA＝E，则A3B＋BA3＝________.

3.13 设A，B，C为n 阶矩阵，且AB＝BC＝CA＝E，则A2＋B2＋C2＝________.

3.14 设B＝（E＋A）（E－A）－1，其中A＝，则（E＋B）－1＝________.

3.15 设n阶矩阵A，满足A2－2A＋5E＝O，则（A＋E）－1＝________.

3.16 设A＝E＋αβT，其中α＝［a1，a2，a3］T，β＝［b1，b2，b3］T，且αTβ＝3，则A－1＝________.

3.17 已知A3＝2E，B＝A2－2A＋2E.证明B可逆，并求出其逆矩阵.

3.18 设A，B是n 阶方阵，E＋AB 可逆，证明：E＋BA 的逆矩阵是E－B（E＋AB）－1A.

3.19 设A，B均为n 阶矩阵，且B和E－AB 都是可逆矩阵，证明：E－BA 可逆.

3.20 设M 是m×n矩阵，MMT可逆，P＝E－MT（MMT）－1M，证明：（1）PT＝P；（2）P2＝P.

3.21 设A是2阶矩阵.

（1）命题“若A2＝O，则A＝O”是否正确.若正确，证明之；若不正确，举例说明；

（2）求满足A2＝O的所有的A；

（3）若A2＝O且AT＝A，证明：A＝O.

3.22 设A 是n（n＞2）阶矩阵，A*是A 的伴随矩阵，k≠0，k≠1，则（kA）*＝（）.

（A）kA*（B） （C）kn－1A*（D）knA*

3.23 设A，B是n 阶方阵，已知|A|＝2，|E＋AB|＝3，则|E＋BA|＝________.

3.24 设n阶矩阵A 与n 阶矩阵B 等价，有（）.

（A）|A|＝a≠0，则|B|＝a（B）|A|＝a≠0，则|B|＝－a

（C）|A|＝a≠0，则|B|＝0（D）|A|＝0，则|B|＝0

3.25 设A，B，C为n 阶方阵，满足A＝BC，将A，B按列分块，记

［α1，α2，…，αn］＝［β1，β2，…，βn］C.

下列选项中使得上式等号保持不变的是（）.

（A）将αi 和αj 互换后，应将βi，βj 互换

（B）将βi 和βj 互换后，应将C的第i行和第j行互换

（C）将αi 加到αj 后，应将βi 加到βj

（D）将βi 加到βj 后，应将C的第i行加到第j行

3.26 设，且，则A*B＝________.

3.27 设，其中a≠b，则与A可交换的矩阵是________.

3.28 求与可交换的全部2阶矩阵.

3.29 设

问是否存在非单位矩阵B，使得AB＝A？若不存在，请说明理由；若存在，求出所有满足AB＝A的B.

3.1 【解】（1）QP＝

（2）A＝PMQ，An＝（PMQ）n＝PMQPMQ…PMQ＝PM（QP）M（QP）M…M（QP）MQ.

由（1）知，QP＝E，代入上式，得

【注】实际上，本题是利用A相似于对角矩阵，以及对角矩阵的n次幂来计算An.

3.2 【分析】将（A＋E）k直接展开.

【证】因E和任意矩阵可交换，则（A＋E）k＝（E＋A）k，且Em＝E，又A2＝A，可得Am＝A，由二项式展开直接可得

【注】本题因与正整数k有关，故也可用数学归纳法证明.

3.3 【解】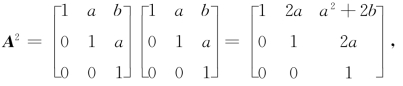

假设当n＝k时，

成立，则当n＝k＋1时，

由第一数学归纳法，知

3.4 【证】（E－A）（E＋A）*＝［2E－（E＋A）］（E＋A）*

＝2E（E＋A）*－（E＋A）（E＋A）*

＝（E＋A）*2E－（E＋A）*（E＋A）

＝（E＋A）*［2E－（E＋A）］

＝（E＋A）*（E－A）.

【注】（1）公式AA*＝A*A＝E 中的A 是任意阶方阵.将E＋A代入，即有

（E＋A）（E＋A）*＝（E＋A）*（E＋A）.

（2）若E＋A是可逆矩阵，则有（E－A）（E＋A）－1＝（E＋A）－1（E－A）.

3.5 【证】AB＝A－B，得（A＋E）B＝A＝A＋E－E，即

（A＋E）（B－E）＝－E，（A＋E）（E－B）＝E，

则A＋E，E－B互为逆矩阵，故有

（A＋E）（E－B）＝（E－B）（A＋E）＝E，
A＋E－BA－B＝E，

即BA＝A－B，得证BA＝A－B＝AB.

【注】由可逆矩阵的定义：若AB＝BA＝E，则A，B为可逆矩阵，且互为逆矩阵.故可逆矩阵与其逆矩阵是可交换矩阵，从而有（A＋E）（E－B）＝E＝（E－B）（A＋E），这是本题证明的关键.(www.chuimin.cn)

3.6 【证】由题设AT＝A，BT＝B.

（1）因（A＋B）T＝AT＋BT＝A＋B，故A＋B是对称矩阵.

（2）充分性.（AB）T＝BTAT＝BA，当AB＝BA 时，有（AB）T＝BA＝AB，故AB 是对称矩阵.必要性.当AB 是对称矩阵，即（AB）T＝AB 时，因（AB）T＝BA，故有AB＝BA，即A，B可交换.

3.7 【证】（1）（A＋AT）T＝AT＋（AT）T＝A＋AT，故A＋AT是对称矩阵；

（A－AT）T＝AT－（AT）T＝AT－A＝－（A－AT），故A－AT是反对称矩阵.

（2）方法一 由（1）知，对任意n阶方阵A，可得是对称矩阵，是反对称矩阵，故有

方法二 设A可表示成

其中，B是对称矩阵，即有BT＝B，C是反对称矩阵，即有CT＝－C，则

由①＋②，得，由①－②，得，其中

故A＝B＋C＝，得证.

【注】这和高等数学中任一函数f（x）一定可以表示成一个奇函数和一个偶函数之和类同.

3.8 【分析】即证f（A）T＝－f（A）.

【证】f（A）T＝［（E－A）（E＋A）－1］T＝［（E＋A）－1］T（E－A）T

＝［（E＋A）T］－1（ET－AT）＝（E＋AT）－1（E－AT）.

由题设条件AAT＝E，即AT＝A－1，代入上式，得

故f（A）是反对称矩阵.

【注】（*）处由习题3.4的“注”中的“（2）”可知（A＋E）－1和E－A可交换.

3.9 【证】充分性.设A是反对称矩阵，即AT＝－A，又对任意的x，xTAx 是一个数，有

xTAx＝（xTAx）T，

而 （xTAx）T＝xTATx＝－xTAx，

从而有2xTAx＝0，即对任意x，均有xTAx＝0.

必要性.设

对任意x＝［a1，a2，…，an］T，有xTAx＝0，故取

x＝ei＝［0，0，…，1，…，0］T，

有 eiTA ei＝aii＝0，i＝1，2，…，n.

取x＝［0，…，1，0，…，1，0，…，0］T＝ei＋ej，得

（ei＋ej）TA（ei＋ej）＝eTiAei＋eTiAej＋eTjAei＋eTjAej＝aij＋aji＝0，

从而有aij＝－aji，i≠j，i，j＝1，2，…，n，故A是反对称矩阵.

【注】（1）不习惯于取x＝［0，0，…，1，…，0］T，x＝［0，…，1，0，…，1，0，…，0］T的读者，可以取x＝［1，0，…，0］T，x＝［1，1，0，…，0］T证明之，再推广到一般.

（2）有的读者认为，A是n阶矩阵，对任意的n维列向量x，有xTAx＝0，则A＝O.由上述证明可知这是错误的.若改为“A是n阶实对称矩阵”，或改为“对任意的n阶方阵B，有BTAB＝O，则A＝O”，此时，结论是正确的.

提示：①若A为n 阶实对称矩阵，则aij＝aji.

仿本题证明过程即可得aij＝aji＝0，aii＝0，于是A＝O.

②若B为任意n阶方阵，由本题证明过程得到启发，将的第一列元素取为

x1＝［0，…，1，…，1，…，0］T＝ei＋ej，第二列元素取为x2＝［0，…，1，…，－1，…，0］T＝ei－ej.于是，由BTAB＝O，得

（ei＋ej）TA（ei－ej）＝eTiAei－eTiAej＋eTjAei－eTjAej＝aii－aij＋aji－ajj＝aji－aij＝0.

又aij＋aji＝0，故aij＝aji＝0，且aii＝0，从而A＝O.

3.10 （1）【解】因AA*＝A*A＝|A|E，故

其中0为n维行向量.

（2）【证】由（1）可得 |PQ|＝|A|2（b－αTA－1α），而|PQ|＝|P||Q|，且|P|＝|A|≠0，故|Q|＝|A|（b－αTA－1α）.

由此可知，|Q|≠0的充分必要条件为αTA－1α≠b，即矩阵Q可逆的充分必要条件是αTA－1α≠b.

【注】本题考查分块矩阵的运算，注意看清αTA－1α是一个数.

3.11 【解】应填O.

因，知aij＝0，i＝1，2，…，n；j＝1，2，…，n.故A＝O.

3.12 【解】应填A2.

3.13 【解】应填3E.

因AB＝BC＝CA＝E，知A＝B－1＝C－1，B＝A－1＝C－1，C＝A－1＝B－1，A2＝AB－1＝AA－1＝E，同理B2＝BB－1＝E，C2＝CC－1＝E，故A2＋B2＋C2＝3E.

3.14 【解】应填

3.15 【解】应填－

由于A2－2A＋5E＝（A＋E）（A－3E）＋8E＝O，则

3.16 【解】应填

令B＝αβT，则B2＝（αβT）（αβT）＝α（βTα）βT＝3B，这里βTα＝αTβ＝3，所以（A－E）2＝3（A－E），即A2－5A＋4E＝O，故，得

3.17 【证】将2E＝A3代入B的表达式得到

B＝A2－2A＋A3＝A（A2＋A－2E）＝A（A＋2E）（A－E）.

若能证明A，A＋2E及A－E可逆，且又能分别求出其逆矩阵，就证明了B可逆，其逆矩阵也就能求出.事实上：

①由A3＝2E得到A3－E＝E，即（A－E）（A2＋A＋E）＝E，故A－E可逆，且（A－E）－1＝A2＋A＋E；

②由A3＝2E 得到A（A2／）2＝E，故A可逆，且A－1＝A2／2；

③由A3＝2E 得到A3＋23E＝2E＋23E＝10E，即

（A＋2E）［（A2－2A＋4E）／10］＝E，

故A＋2E 可逆，且（A＋2E）－1＝（A2－2A＋4E）／10.

因A，A＋2E，A－E 可逆，故其乘积B＝A（A＋2E）（A－E）可逆，且

B－1＝［A（A＋2E）（A－E）］－1＝（A－E）－1（A＋2E）－1A－1

＝（A2＋A＋E）（A2－2A＋4E）A2／20

＝（A6－A5＋3A4＋2A3＋4A2）／20

＝（4E－2A2＋6A＋4E＋4A2）／20

＝（A2＋3A＋4E）／10.

3.18 【证】因（E＋BA）［E－B（E＋AB）－1A］＝E＋BA－B（E＋AB）－1A－BAB（E＋AB）－1A

＝E＋BA－B（E＋AB）（E＋AB）－1A

＝E＋BA－BA＝E，

故（E＋BA）－1＝E－B（E＋AB）－1A.

3.19 【证】

故E－BA 可逆.

3.20 【证】（1）PT＝［E－MT（MMT）－1M］T＝ET－MT［（MMT）－1］TM

＝E－MT［（MMT）T］－1M＝E－MT（MMT）－1M＝P.

（2）P2＝［E－MT（MMT）－1M］［E－MT（MMT）－1M］

＝E－2MT（MMT）－1M＋MT（MMT）－1MMT（MMT）－1M

＝E－2MT（MMT）－1M＋MT（MMT）－1（MMT）（MMT）－1M

＝E－2MT（MMT）－1M＋MT（MMT）－1M＝E－MT（MMT）－1M＝P.

3.21 （1）【解】“若A2＝O，则A＝O”是错误的.例，有A2＝O，但A≠O.

（2）【解】设，由A2＝O得，即

解得d＝－a，bc＝－a2，故，其中a为任意实数，b，c为满足bc＝－a2的任意实数.

（3）【证】利用（2）的结论，当AT＝A时，可设且b2＝－a2，解得a＝b＝0.

故满足A2＝O且AT＝A的矩阵为A＝O.

【注】（1）要说明命题不成立，只要举出反例即可，举反例越简单越好，只要能说明问题就行.

（2）证明A＝O，一般有两种途径：①证aij＝0（如本题（3））；②证r（A）＝0或直接证A＝O.

3.22 【解】应选（C）.

方法一 由A*的定义直接计算（kA）*.设A＝（aij）n×n，Aij 是|A|中元素aij 的代数余子式，则

故应选（C）.

方法二 由AA*＝|A|E，当A可逆时，有A*＝|A|A－1，且

故应选（C）.

方法三 逐项验算是否符合（kA）（kA）*＝|kA|E＝kn|A|E.

（A）（kA）kA*＝k2AA*＝k2|A|E≠kn|A|E；

（B）（kA）＝AA*＝|A|E≠kn|A|E；

（C）（kA）kn－1A*＝knAA*＝kn|A|E；

（D）（kA）knA*＝kn＋1AA*＝kn＋1|A|E≠kn|A|E.

综上所述，应排除（A），（B），（D），故选（C）.

【注】（1）本题是计算型选择题，典型解法有两种：①直接计算，方法一是按定义直接计算，方法二是按公式直接计算；②逐项验算（方法三）.

（2）对于选择题，方法一中计算3阶矩阵即可，方法二中可设A－1存在，因命题中的关系，对3阶、对可逆也应成立，方法三中最多验算三项即可.

（3）（kA）*＝kn－1A*可作公式应用，例如（－A）*＝（－1）n－1A*.

3.23 【解】应填3.

方法一 由|A|＝2≠0，知A可逆，故E＋BA＝（A－1＋B）A＝A－1（E＋AB）A.

两边取行列式，得|E＋BA|＝|A－1（E＋AB）A|＝|A－1||E＋AB||A|＝|E＋AB|＝3.

方法二 因A（E＋BA）＝A＋ABA＝（E＋AB）A，两边取行列式，得

|A||E＋BA|＝|E＋AB||A|，|A|＝2≠0，

故|E＋BA|＝|E＋AB|＝3.

3.24 【解】应选（D）.

方法一 A和B 等价⇔存在可逆矩阵P，Q，使得PAQ＝B.两边取行列式，得

|PAQ|＝|P||A||Q|＝|B|，

P，Q可逆，|P|≠0，|Q|≠0，但不知具体的数值，故当|A|＝a≠0时，|B|的值无法确定，排除（A），（B），（C）.但当|A|＝0时，必有|B|＝|P||A||Q|＝0，故选（D）.

方法二 A和B等价，A经过若干次初等变换后化成B（可以是行变换，也可以是列变换）.

三类初等变换：①互换变换改变行列式的正负；②倍乘变换将行列式扩大（缩小）k（k≠0）倍；③倍加变换不改变行列式的值.当|A|＝0时，经过①改变正负，②扩大（缩小）k（k≠0）倍，③保持不变，仍有|B|＝0（当|A|≠0时，|B|的值无法确定），故选（D）.

3.25 【解】应选（B）.βi 和βj 互换后，应将C 的第i行和第j行互换，因

［α1，α2，…，αn］＝［β1，β2，…，βn］C

＝［β1，β2，…，βn］EijE－1ijC

＝（［β1，β2，…，βn］Eij）（EijC）.

3.26 【解】应填

B是由A 的第1列的（－2）倍加到第3列，然后再互换第1列和第2列得到，记

则B＝AP1P2，于是A*B＝A*AP1P2＝

3.27 【解】应填，其中x1，x4 是任意常数.

设与A可交换的矩阵是，则

对应元素相等，得 ax2＝bx2，（a－b）x2＝0；bx3＝ax3，（a－b）x3＝0.

因a≠b，故x2＝x3＝0.

故与对角元素互不相同的对角矩阵可交换的矩阵是对角矩阵，其中x1，x4是任意常数.

【注】与对角矩阵可交换的矩阵是对角矩阵，即对角矩阵和对角矩阵可交换.

3.28 【解】设与A可交换的2阶矩阵为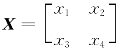，则根据题意，有

对应元素相等，得

解得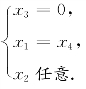

故与可交换的2阶矩阵为

【注】（1）不是任意矩阵都可以与A交换，而是有一部分矩阵可与A交换.本题是用待定系数（待定矩阵）法解矩阵方程，从而求出与A可交换的所有2阶矩阵.

（2）因单位矩阵E 可与任何矩阵交换，故将A分解为

则求与A可交换的矩阵，即求与C可交换的矩阵，且C形式简单，更便于计算.

3.29 【解】令AB＝A，即A（B－E）＝O，因B≠E，则B－E≠O，故当A可逆时，Ax＝0有唯一零解，不存在B（B≠E），使得AB＝A.当A不可逆时，Ax＝0有非零解，存在B（B≠E），使得AB＝A成立.

因

故A不可逆，且Ax＝0有通解x＝k［1，－1，1］T，其中k为任意常数.

对于不全为零的任意常数k1，k2，k3，有

则

且使AB＝A成立.