首页理论教育初等矩阵定义及特点-张宇线性代数9讲

初等矩阵定义及特点-张宇线性代数9讲

2023-11-21 理论教育版权反馈

【摘要】：（1）定义（Eij，Eij（k），Ei（k））.①初等变换.（ⅰ）一个非零常数乘矩阵的某一行（列）.（ⅱ）互换矩阵中某两行（列）的位置.（ⅲ）将矩阵的某一行（列）的k倍加到另一行（列）.以上三种变换称为矩阵的初等行（列）变换，且分别称为倍乘、互换、倍加初等行（列）变换.②初等矩阵.由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵.以3阶矩阵为例，并随之给出定义.（ⅰ）E2（k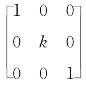）＝，E 的第2行（或

（1）定义（Eij，Eij（k），Ei（k））.

①初等变换.

（ⅰ）一个非零常数乘矩阵的某一行（列）.

（ⅱ）互换矩阵中某两行（列）的位置.

（ⅲ）将矩阵的某一行（列）的k倍加到另一行（列）.

以上三种变换称为矩阵的初等行（列）变换，且分别称为倍乘、互换、倍加初等行（列）变换.

②初等矩阵.

由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵.以3阶矩阵为例，并随之给出定义.

（ⅰ）E2（k）＝ pagenumber_ebook=48,pagenumber_book=40 ，E 的第2行（或第2列）乘k倍，称为倍乘初等矩阵.

定义：Ei（k）（k≠0）表示单位矩阵E 的第i行（或第i列）乘非零常数k所得的初等矩阵.

（ⅱ）E12＝ pagenumber_ebook=48,pagenumber_book=40 ，E 的第1行与第2行（或第1列与第2列）互换，称为互换初等矩阵.

定义：Eij 表示单位矩阵E 交换第i行与第j行（或交换第i列与第j列）所得的初等矩阵.

（ⅲ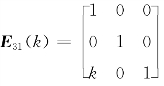） pagenumber_ebook=49,pagenumber_book=41 ，E的第1行的k倍加到第3行（或第3列的k倍加到第1列），称为倍加初等矩阵.

定义：Eij（k）表示单位矩阵E的第j行的k倍加到第i行（或第i列的k倍加到第j列）所得的初等矩阵.

【注】也有教材将Eij（k）表示E的第i行的k倍加到第j行，故考研中所有初等变换的描述均用文字描述代替，以避免出现不同教材中不同的提法所带来的不同定义，考生掌握本质即可，不必纠结于此.考试中以“P，Q”来表示，为统一不引起歧义.

（2）性质.

①

②ETij＝Eij，ETij（k）＝Eji（k），ETi（k）＝Ei（k）.

③E－1ij＝Eij，E－1ij（k）＝Eij（－k），E－1i（k）＝

④Eij*＝

Eij*（k）＝

E*i（k）＝

（3）左行右列定理.

矩阵A左乘初等矩阵P，得PA，相当于对A作了一次与P 完全相同的初等行变换；矩阵A右乘初等矩阵P，得AP，相当于对A作了一次与P 完全相同的初等列变换.(www.chuimin.cn)

见例3.17，例3.18.

（4）应用.

①求A－1.

②研究Pm1APn2＝B.

见例3.6.

例3.17 设A是3阶可逆矩阵，交换A的第1列和第2列得到B，A*，B*分别是A，B的伴随矩阵，则B*可由（）.

（A）A*的第1列与第2列互换得到（B）A*的第1行与第2行互换得到

（C）－A*的第1列与第2列互换得到（D）－A*的第1行与第2行互换得到

【解】应选（D）.

交换A的第1列和第2列得到B，即

B＝AE12，

则

B*＝（AE12）*＝E*12A*＝－E12A*＝E12（－A*），

故B*可由－A*的第1行与第2行互换得到，应选（D）.

例3.18 设A为3阶矩阵，将A的第2行加到第1行得到B，再将B的第1列的（－1）倍加到第2列得到C，记

则（）.

（A）C＝P－1AP （B）C＝PAP－1（C）C＝PTAP （D）C＝PAPT

【解】应选（B）.

将A的第2行加到第1行得到B，即

将B的第1列的（－1）倍加到第2列得到C，即

因

故Q＝P－1，从而有C＝BQ＝BP－1＝PAP－1，故应选（B）.