线性代数习题解法+例题讲解

2023-11-21 理论教育版权反馈

【摘要】：，s）均可逆，则A可逆，且见例3.16.例3.12 已知，写出A可逆的一个充要条件，当A可逆时，求A－1.A可逆故当ad－bc≠0时，例3.13 设n阶方阵A 满足A3－2A2＋3A－4E＝O，则A－1＝________.若能找到n阶方阵B，使得AB＝E，则A－1＝B.这样的B应利用题设条件去找.应填由题设条件A3－2A2＋3A－4E＝O，移项得A3－2A2＋3A＝4E，左端提出公因子，得 A＝4E，即故知A可逆，且类似本题的一般问法：设f是多项式，且f＝akxk＋ak－1xk－1＋…

（1）定义.

对于方阵A，B，若AB＝E，则A，B互为逆矩阵，且A－1＝B，B－1＝A，AB＝BA.

（2）性质.

①（A－1）－1＝A.

②（AB）－1＝B－1A－1（穿脱原则）.

③k≠0，k（）A－1＝

④（AT）－1＝（A－1）T.

⑤

（3）求A－1.

①具体型.

（ⅰ）A－1＝

见例3.12.

（ⅱ）

②抽象型.

（ⅰ）由题设式子恒等变形，创造AB＝E，则A－1＝B.

（ⅱ）由题设式子恒等变形，创造A＝BC，若B，C均可逆，则A－1＝C－1B－1.

见例3.13至例3.15.

（4）分块矩阵.

①加法：同型，且分法一致，则 pagenumber_ebook=44,pagenumber_book=36

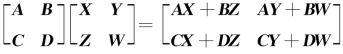②数乘： pagenumber_ebook=45,pagenumber_book=37

③乘法： pagenumber_ebook=45,pagenumber_book=37 ，要可乘、可加.

【注】对于③的运算要注意，分块相乘后，左边的仍在左边，右边的仍在右边.

④若A，B分别为m，n阶方阵，则分块对角矩阵的幂为

⑤已知 pagenumber_ebook=45,pagenumber_book=37 ，其中B是r阶可逆矩阵，C是s阶可逆矩阵，则A可逆，且

【注】若

其中B，C可逆，则有

⑥主对角线分块矩阵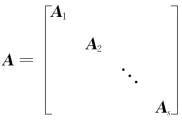 pagenumber_ebook=45,pagenumber_book=37 ，若Ai（i＝1，2，…，s）均可逆，则A可逆，且

副对角线分块矩阵

若Ai（i＝1，2，…，s）均可逆，则A可逆，且

见例3.16.

例3.12 已知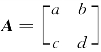 pagenumber_ebook=46,pagenumber_book=38 ，写出A可逆的一个充要条件，当A可逆时，求A－1.

【解】A可逆 pagenumber_ebook=46,pagenumber_book=38 故当ad－bc≠0时，

例3.13 设n阶方阵A 满足A3－2A2＋3A－4E＝O，则A－1＝________.

【分析】若能找到n阶方阵B，使得AB＝E，则A－1＝B（且B－1＝A）.这样的B应利用题设条件去找.

【解】应填

由题设条件A3－2A2＋3A－4E＝O，移项得

A3－2A2＋3A＝4E，

左端提出公因子，得 A（A2－2A＋3E）＝4E，

即(www.chuimin.cn)

故知A可逆，且

【注】（1）类似本题的一般问法：设f（x）是多项式，且f（x）＝akxk＋ak－1xk－1＋…＋a1x＋a0，其中a0≠0，A是n 阶方阵，满足f（A）＝O，则A－1＝________.

同本题，可解得

（2）同本题题设条件（即A满足A3－2A2＋3A－4E＝O），则（A－E）－1＝________.

将题设条件A3－2A2＋3A－4E＝O变形成（凑出）

（A－E）（A2－A＋2E）－2E＝O，

即可得

例3.14 设A，B，A＋B均为可逆矩阵，则（A－1＋B－1）－1等于（）.

（A）A－1＋B－1（B）A＋B （C）A（A＋B）－1B （D）（A＋B）－1

【分析】利用可逆矩阵的乘积仍是可逆矩阵，将（A－1＋B－1）－1表示成已知可逆矩阵A，B，A＋B的乘积.

【解】应选（C）.

A－1＋B－1＝EA－1＋B－1＝B－1BA－1＋B－1＝B－1（BA－1＋E）＝B－1（BA－1＋AA－1）

＝B－1（B＋A）A－1，

又因B－1，A＋B，A－1均为可逆矩阵，故A－1＋B－1＝B－1（A＋B）A－1是可逆矩阵，且

（A－1＋B－1）－1＝［B－1（A＋B）A－1］－1＝A（A＋B）－1B，

故选（C）.

【注】（1）等式A－1＋B－1＝B－1（B＋A）A－1.从右至左是显然的，但从左至右却要一定的技巧，其主要思路是A可逆时，有AA－1＝A－1A＝E，且EA＝A.把等式中的E 替换成AA－1或A－1A，等式中没有E，可以主动乘E，使A＝EA或A＝AE.

（2）本题也可验算得到.

（A－1＋B－1）A（A＋B）－1B＝（E＋B－1A）（A＋B）－1B＝B－1（B＋A）（A＋B）－1B＝B－1B＝E，

故（A－1＋B－1）－1＝A（A＋B）－1B.

应选（C）.

（3）与本题求（A－1＋B－1）－1类似的思路，

A－1＋B－1＝A－1E＋B－1＝A－1BB－1＋B－1＝（A－1B＋E）B－1＝A－1（B＋A）B－1，

故（A－1＋B－1）－1＝B（A＋B）－1A.

这说明A（A＋B）－1B＝B（A＋B）－1A，且均是A－1＋B－1的逆矩阵.

例3.15 设A为n 阶非零矩阵，E 为n 阶单位矩阵，若A3＝O，则（）.

（A）E－A不可逆，E＋A不可逆（B）E－A不可逆，E＋A可逆

（C）E－A可逆，E＋A可逆（D）E－A可逆，E＋A不可逆

【解】应选（C）.

方法一因为A3＝O，故E＝E±A3＝（E±A）（E∓A＋A2），即分别存在矩阵E－A＋A2和E＋A＋A2，使

（E＋A）（E－A＋A2）＝E，（E－A）（E＋A＋A2）＝E，

可知E－A与E＋A都是可逆的，所以应选（C）.

方法二设λ是A 的实特征值，由A3＝O，得λ3＝0⇒λ＝0，故A的实特征值只有0，于是E－A的实特征值只有1，E＋A的实特征值只有1，故二者均可逆.

【注】方法一是利用定义法，方法二是说明0不是特征值.

例3.16 设

求A－1.

【解】将A分块如下，

其中，

线性代数习题解法+例题讲解

相关推荐