首页理论教育线性代数九讲中求余子式问题

线性代数九讲中求余子式问题

2025-09-30 理论教育版权反馈

【摘要】：由于Mij＝（－1）i＋jAij，故先求出Aij，乘（－1）i＋j即可.例2.1 设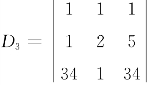，则5A11＋2A12＋A13＝________.应填520.例2.2 已知3阶行列式|A|＝－9，其第2行元素为［1，1，2］，第3行元素为［2，2，1］，则A31＋A32－3A33＝________.应填－15.记，则2A31＋2A32＋A33＝|A|＝－9，而即由解得A31＋A32＝－6，A33＝3，故A31＋A32－3A33＝－15.例2.3 设n阶行列式求：|A|中所有元素aij 的代数余子式Aij 之和A11＋A22＋…

由于Mij＝（－1）i＋jAij，故先求出Aij，乘（－1）i＋j即可.

例2.1 设 pagenumber_ebook=29,pagenumber_book=21 ，则5A11＋2A12＋A13＝________.

【解】应填520.

例2.2 已知3阶行列式|A|＝－9，其第2行元素为［1，1，2］，第3行元素为［2，2，1］，则A31＋A32－3A33＝________.

【解】应填－15.

记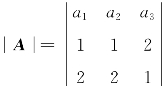 pagenumber_ebook=29,pagenumber_book=21 ，则2A31＋2A32＋A33＝|A|＝－9，而

即由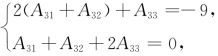 pagenumber_ebook=29,pagenumber_book=21 解得A31＋A32＝－6，A33＝3，故A31＋A32－3A33＝－15.

例2.3 设n阶行列式

求：（1）|A|中所有元素aij 的代数余子式Aij 之和 pagenumber_ebook=30,pagenumber_book=22

（2）A11＋A22＋…＋Ann；

（3）Ak1＋Ak2＋…＋Akn（k＝1，2，…，n）.

|A|＝2n≠0，故A可逆，且

A＝|A|A－1＝2nA－1.

由，有

故有

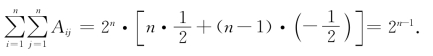
（1） pagenumber_ebook=31,pagenumber_book=23

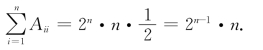
（2） pagenumber_ebook=31,pagenumber_book=23

（3）当k＝1，2，…，n－1时，

当k＝n时，

例2.4 已知3阶行列式|A|的元素aij 均为实数，且aij 不全为0.若

aij＝－Aij（i，j＝1，2，3），

其中Aij 是aij 的代数余子式，则|A|＝________.

【解】应填－1.

由aij＝－Aij 有A＝－AT.于是

AA＝－AAT.

又AA＝|A|E，故

AAT＝－|A|E.

两边取行列式得(https://www.chuimin.cn)

|A||AT|＝－|A|3，即|A|2＝－|A|3，

即

由aij 不全为0，知存在akj≠0，将行列式|A|按第k行展开得

|A|＝ak1Ak1＋ak2Ak2＋ak3Ak3

＝－a2k1－a2k2－a2k3＜0.

故由（）式，知|A|＝－1.

例2.5 已知3阶方阵A的特征值为－1，2，3，则A11＋A22＋A33＝________.

【解】应填1.

记λ1＝－1，λ2＝2，λ3＝3，由本讲的“三”，有

A11＋A22＋A33＝tr（A）＝λ1＋λ2＋λ3

＝λ2λ3＋λ1λ3＋λ1λ2

＝2×3＋（－1）×3＋（－1）×2

＝6－3－2＝1.

2.1 设

则A41＋A42＋A43＋A44＝___________.

2.2 设

则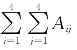 pagenumber_ebook=32,pagenumber_book=24 ＝________.

2.3 设n阶行列式

Aij 是Dn 中元素aij（i，j＝1，2，…，n）的代数余子式，求Dn 的全部代数余子式之和.

2.1 【分析】A4j是第4行元素a4j（j＝1，2，3，4）的代数余子式，其值只与第1，2，3行元素有关，与第4行元素无关.

【解】应填－9.

将|A|中的第4行元素依次换为1，1，1，1，并不改变A4j（j＝1，2，3，4）的大小，有

2.2 【解】应填

【注】本题若命制成“设4阶行列式|A|的某行元素全为2，且|A|＝a，计算”估计会增加一些难度，但解法和过程与本题完全一样，只不过要求读者多写一句“不妨设|A|的第一行元素全为2”即可.应对考试，读者一定要多从命题人的角度出发，想想看如何“变着花样”出题，知己知彼，才是科学的复习策略.

2.3 【解】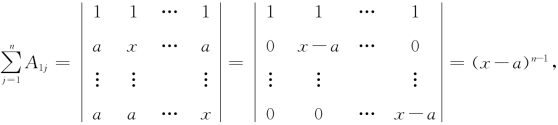 pagenumber_ebook=33,pagenumber_book=25

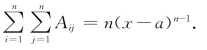
同理， pagenumber_ebook=34,pagenumber_book=26 故